信号链基础：时钟抖动解秘――高速链路时钟抖动规范基础知识分享
用于在更远距离对日益增长的海量数据进行传输的一些标准不断出现。来自各行业的工程师们组成了各种委员会和标准机构，根据其开发标准的目标（数据吞吐量和通信距离）确定抖动预算；同时还要考虑到组成通信链路的模块的局限性。
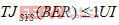方程式 1其中：TJSYS 是总抖动，而 1UI 为1个单位时间间隔（1 比特时间）
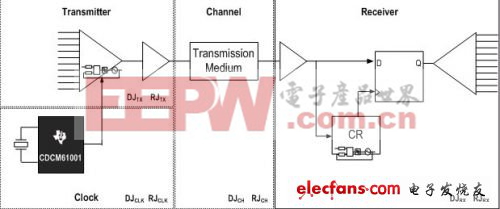
总抖动 (TJ) 包括每个子系统决定性抖动和随机抖动的和。由于随机抖动自身的属性，进行这种求和时需要特别注意。随机抖动呈现高斯（随机）分布，并且无边界。因此，随机抖动可表示为一个 RMS 值，并且在规定测量/整合带宽范围内对其进行估算。例如，图1 所示接收机的抖动测量带宽便为 f2 - f1（参见图2）。这是因为接收机锁相环路 (PLL) 追踪 f1 以下的抖动（从而排斥它），而发射 PLL 的频率上限为 f2。从接收机的角度来看，使链路性能降低的随机抖动降至这些限制之间。
由于随机抖动是随机过程产生的结果，系统总随机抖动的计算需要进行方和根 (RSS) 计算，如方程式2所示：
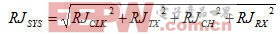方程式2决定性抖动源和的计算很简单：
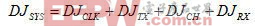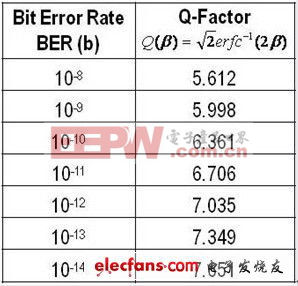
方程式 3最后，可对系统总抖动进行估算，由此可以实现链路预算；但是，还需要做更多的工作。这种计算涉及统计数学。需要用到一种被称之为 Q 因数的参数（参见表 1）。Q 因数的大小具体取决于误码率 (BER)，同时还要根据链路性能/可靠性目标来选择。由于随机抖动的无边界属性，（最终）会出现误码。例如，10-8 的 BER 意味着，每发送 100,000,000 比特便会有一个比特被错误解释。现代的通信系统通常会要求一个达到或者超过 10-12 以上的 BER。
系统总抖动（以及链路预算）可使用方程式 4 计算得到：
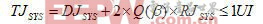方程式4例如，10-14 的 BER 时，总抖动为：
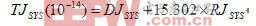方程式 5表1Q 因数和误码率
本文讨论了构成总抖动预算的一些参数。下一次，我们将探讨时钟，并研究随机抖动和相位噪声之间的关系。
评论