基于提升小波的毫米波信号实时去噪*

　　引言

　　毫米波具有抗干扰能力强、精度高、低仰角探测性能好、能够穿透等离子体等优点，已广泛应用于军事、民用等领域。在天线口径相同条件下，3mm波段毫米波探测器相对其它波段具有波束窄、探测距离远、目标定位准确等优点[1]。然而探测器回波信中含有各种噪声干扰，需进行去噪处理，选用适当的去噪方法可尽量减少噪声对目标识别结果的影响。小波分析与傅立叶分析相比，具有良好的时频局部特性和多分辨分析特性，在去噪领域应用广泛。传统小波的构造是以傅立叶变换为基础，而提升格式小波变换则是直接在时域分析问题，完全脱离了傅立叶变换,并且所有传统小波都可以通过提升方法构造出来[2]。Koichi Kuzume等人实现了基于FPGA的提升小波实时信号处理[3];A.R.Calderbank、Michael D.Adams等研究了整数小波变换及整数提升小波变换[4][5];国内很多人研究了基于提升格式小波变换的信号去噪[6][7]。采用提升小波进行信号去噪，运算速度快，耗费存储空间少，可实现整数小波变换，易满足信号处理的实时性要求。

　　3mm波段毫米波探测器小型化应用时信号处理系统的硬件平台浮点处理能力差，要求去噪算法最好为整数间的运算，考虑信号处理的实时性，算法的复杂度要适合硬件平台的运算速度。本文选用5/3小波在基于TMS320VC5509A型DSP的硬件平台上实现了毫米波探测器回波信号的实时去噪处理。

　　提升小波变换

　　提升小波变换由三个基本步骤构成：(1)分解，将原始离散信号分割为两个互不相交的子集，例如将信号x(n)按位置分为奇偶序列xo(2n+1)和xe(2n)，即常用的lazy小波变换。(2)预测，又称对偶提升。定义预测算子P来产生小波系数d，其表达式为：d=xo-P(xe)，即用xe去预测xo产生的误差。由于信号有局部相关性，信号某一点的值可以通过其相邻的值经合适的预测算子来预测，预测误差就是信号的高频信息。(3)更新，又称原始提升。通过更新算子U产生尺度系数c，其表达式为：c=xe+U(d)，即用d来调整信号的下采样xe，得到信号的低频分量。以上三个步骤为提升小波变换的前向变换，而逆向变换只需改变前向变换公式中的正负号和颠倒计算步骤次序。

　　5/3小波是具有对称结构的双正交小波，其分解端与重构端的滤波器长度分别为5和3，消失矩都为2，广泛应用于滤波及图像处理等领域。其提升系数分别为α=-1/2，β=1/4,可表示为1/2n(n为整数)，运算过程只含有加法和移位运算，大大加快了运算速度，利于通用计算机以外的硬件平台的实现。基于整数的5/3小波算法步骤为：

　　(1)xo(n)=x(2n+1)，xe(n)=x(2n)

　　(2)d1(n)=xo(n)+int(α(xe(n)+xe(n+1))+1/2)

　　(3)c1(n)=xe(n)+int(β(d1(n)+d1(n-1))+1/2)

　　其中int(·)表示取整运算。

　　回波信号去噪效果分析

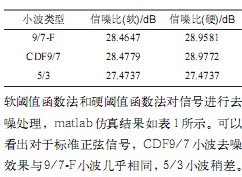
　　小波域阈值滤波法实现简单，计算量小，是目前应用最广泛的一种小波去噪算法，可分为软阈值函数法和硬阈值函数法。软阈值函数法是将绝对值小于阈值的小波系数替换为零，绝对值大于阈值的小波系数用阈值来缩减，其表达式为：

　　硬阈值函数法是将绝对值小于阈值的小波系数替换为零，绝对值大于阈值的小波系数保持不变，其表达式为：