系统电源中保持开关稳定的临界模式控制器的设计

摘要：开关电源中在动态负载的情况下为保持开关稳定，需要将电源系统设计在临界模式下工作，本文中，以FLYBACK拓扑结构为例，分析了临界状态产生的原理，并根据非连续模式和连续工作模式对应的极点和零点，提出了基于开关频率调整的临界模式控制器的设计，通过SPICE模拟，得到了相关结果，在此基础上设计了应用临界模式控制器的开关电源。
关键词：临界模式控制器；开关电源；FLYBACK拓扑结构；SPICE模拟

前言

　　目前，系统中的开关电源具有两种不同的工作模式，当电源处于导通状态的时候，可以用不同的模式来描述环绕在电源扼流圈中的电流[1]。本文以FLYBACK拓扑结构为例，按照其工作原理，可能工作在两种不同的模式，但这两种模式具有相同的功率容量，则对应这两种不同的导通模式，在直流和交流情况下会有非常大的差别，而且组成电源的元器件会受不同程度的影响[2]。根据众多实验结果的分析，可以看出众多的离线式电源系统，为了提高系统的可靠性，降低对元器件等级的要求，一般都工作在非连续区域。

　　本文将首先介绍临界模式控制原理，在分析两种模式工作特点的基础上，提出临界模式控制的概念，并通过不同模式零、极点的分析，得出针对FLYBACK结构调整临界模式的方案，提出整体电路系统设计，并给出模拟仿真结果。

临界模式控制原理

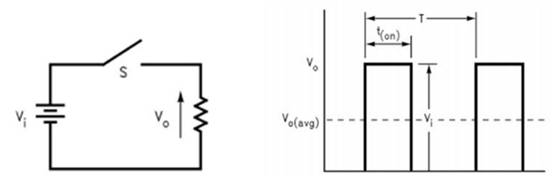
　　图1(a)和(b)示出几个周期内转换器线圈中流过电流的波形示意图，从图中可以看出，当处于导通状态的时候，在电感中建立起来磁场，电流快速上升；而当关断后，电感磁场快速下降，根据洛仑兹定律，在电感中建立起反向电动势，在这种情况下，电流为了保持其电流连续性，必须找到其相应通路，并且电流开始减小，例如，在拓扑结构为FLYBACK的情况下，可以通过输出网络维持其电流，而在BUCK拓扑结构下，则通过续流二极管维持其电流[3]。

　　如果在电流下降的周期内，在电流减至零之前，电路再次导通的话，如图1(a)所示，称为“连续导通模式”（CCM）。而如果当关断时期内，由于线圈储能比较有限，导致再次开通之前电流已经降为零，如图1(b)所示，出现了一段“死区时间”，则对应的工作状态称为“非连续导通模式”（DCM）。死区时间有长有短，而如果将电路设置成这样的工作状态，就是当在关断期间，电流一降到零，系统立即开启，则对应的死区时间为零，对应的这种工作状态称为“临界导通模式”。

图1 开关过程电流示意图

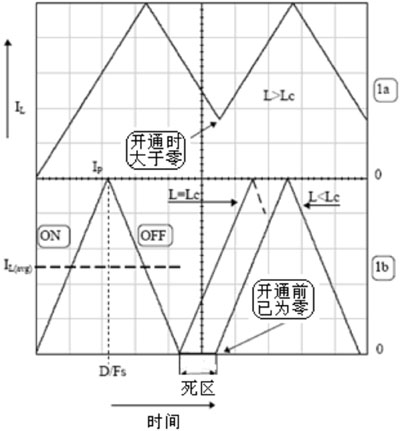
(a)连续导通模式（CCM）电流波形示意图
(b)非连续导通模式（DCM）电流波形示意图

　　目前总共有三种方法使电路进入临界状态：

　　·确定出临界状态对应的电感值LC，但是当电感值LC确定后，在不同负载情况下，系统却可能进入CCM模式，也可能进入DCM模式；
　　·已知的某一个给定电感L情况下，通过确定负载的大小，使电路进入不同的模式；
　　·将上述的电感和电阻等关键元器件的值都固定下来，通过开关频率的调整，使电路进入临界模式。

临界模式控制器的设计

　　图2所示FLYBACK拓扑结构的转换器，通过对它的计算分析来进行进一步的解释。

　　为了简化分析，先进行如下假设[3]：

　　假设1：每周期内电感平均电压降为0；

　　假设2：根据图1(b)所示，当L=LC的时候，IL(平均)=1/2IP

　　假设3：电源功率具有100%的转换效率，即Pin=Pout

　　采用上面假设1，可以确定出在CCM模式下的直流电压转换率，根据图2(b)可以得到下列关系式：

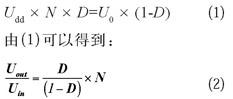
图2 确定临界状态电路示意图


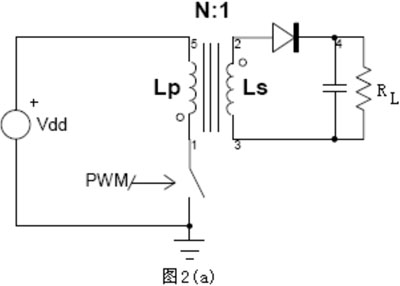
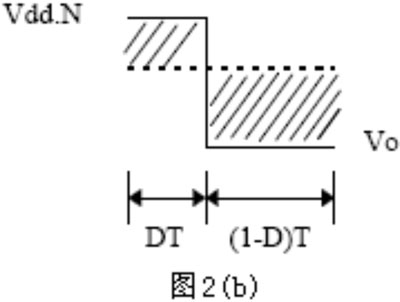
(a) FLYBACK拓扑结构电路示意图
(b) 次级线圈对应电压波形示意图

　　根据图1(b)可以看出，对应于临界模式，意味着在导通状态中，对线圈中存储的能量会在下个周期开始的时候正好降为零，根据此判断，可得[4]：

　　

　　根据假设2，对上式积分可得：

　　，
　　
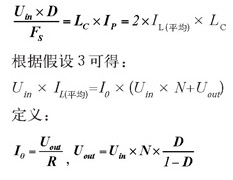
　　通过联立上述方程，可确定出对应临界状态的关键元器件的大小：
　　

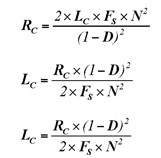
表1 FLYBACK拓扑不同模式对应极点、零点及电压增益

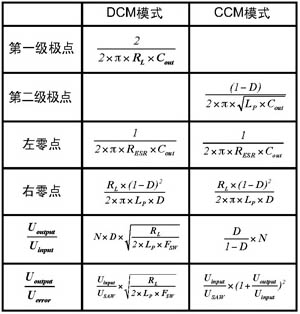
　　以上确定了FLYBACK拓扑结构转换器临界模式对应的关键参数值，也可以确定出，在保证电源稳定和可靠的前提下，DCM模式和CCM模式对应的极点和零点也能够确定出来。表1给出了不同操作模式下极点和零点的位置及对应的FLYBACK电压增益。

　　表1中FSW为开关频率，VSAW对应PWM控制信号锯齿波的幅度，LP为初级线圈电感。

　　根据表1，采用功率分析软件POWER 4-5-6进行模拟[5]，对于100kHz频率、电压模式PWM控制器进行模拟分析，所得结果如图3所示，其中图3(a)所示为DCM模式下的高频极点，图3(b)所示为CCM模式下的高频极点模拟结果。

　　从图3可以看出，DCM模式下，需要双极点单零点的补偿网络，而CCM模式则需要双极点双零点的补偿网络，当在DCM模式下的极点和零点固定的情况下，CCM的二级极点将会对应于控制信号的占空比而发生变化。

控制器的SPICE模拟

　　在用SPICE模拟器进行模拟的时候，这种电源系统对应有两个SPICE模型[5]，一个是平均模型，另一个是开关模型。平均模型使用的是SSA技术，其中没有开关元器件的考虑，所以模拟起来速度快，可以进行交流和瞬态分析。而开关模型中，则更多考虑所用的PWM控制器和其中的开关管MOSFET的特性，能够针对小信号或大信号瞬态扫描进行分析。两种模型各有特点，平均模型仿真速度快，但对电路漏电流和寄生效应等的模拟则无法进行；而开关模型则运行时间较长，但考虑了其中的寄生参数，能够保证对研究的电路进行深入的分析[6]。

图3 对应图2电路的模拟结果

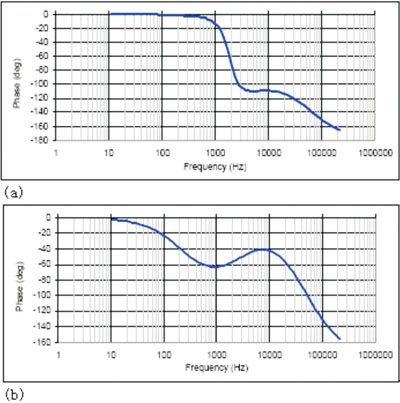
(a) CCM模式下的模拟结果；
(b)DCM模式下的模拟结果

　　本文中，所对应开关模型的网表如下所示：

表2


　　该网表所对应电路如图4所示。

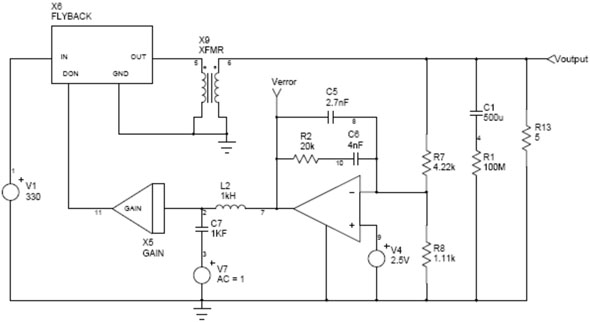
图4 开关模型分析的网表所对应的电路示意图

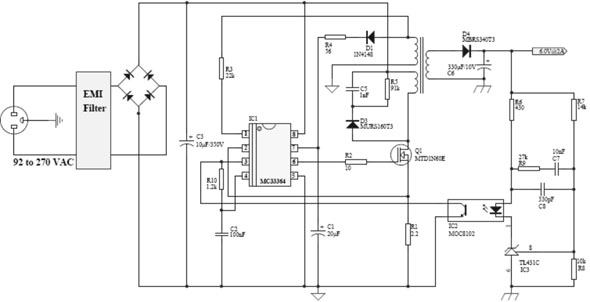
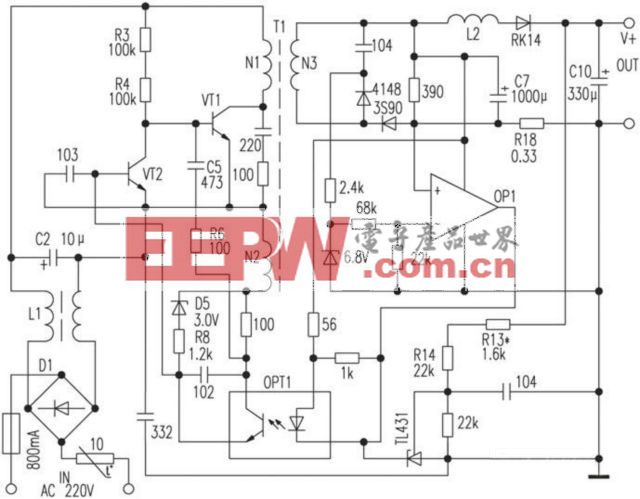
图5 所设计的带有临界模式控制器的开关电源示意图

　　在进行AC模拟的时候，需要暂时反馈开路，将误差放大器隔离开，通过补偿网络的调整，使要求得到满足。最快的方法是如图4中所示，由L2和C7组成的LC网络插入进电路中，达到隔离反馈的目的。电感元件能够维持直流误差的大小，从而使输出维持在所需要的值上，同时将AC误差隔离阻断。电容元件能够产生一个AC信号，从而允许正常的AC扫描。在正常的交流扫描时，使L2=1kH，C7=1kF；而当进行瞬态分析的时候，则L2=1nH，C7=1pF；以上这种办法能够保证自动直流占空比调整，保证当占空比改变的时候，能够快速调整输出参数，而不会对其它信号产生影响。

结论

　　按照前面的讨论，如果将SMPS置于非连续模式，对于涉及补偿网络是相对容易的，而且将电路置于非连续模式能够保证稳定和可靠的电路工作状态。那么如何保证电路在DCM状态，而且与输出无关呢？有两种办法：一是计算LP；二是通过频率的不断调整使电路维持在DCM状态。按照上述方法设计的临界状态控制器能够保证电源电路当初级电路降为零的时候立刻开启，在这种情况下，就不用考虑不同负载情况下的不同设计方法了，只需要保证所设计的控制器能一直控制SMPS在DCM模式下工作即可，而且在很宽的负载范围内都能够稳定可靠工作。

　　另外在设计调整器的时候，还需要考虑特殊情况，例如空载。在这种情况下，按原先设定的控制方案，电路开关频率将被调制的非常高，导致了不必要的开关损耗以及电磁兼容等问题，而且电源在系统工作时，空载情况会非常多见，所以需要在电路设计中解决这一问题，在电路中加了频率钳制器，使频率可调范围的上限在合理范围内。

　　带有临界模式控制器功能的开关电源能够实现400W的AC/DC适配器的调节。其中，漏电部分的控制通过R5和C5(见图5)进行控制，同时还可以对上升电压进行平滑作用，减小了辐射噪声的产生，原来的电路设计中，总是用可控硅和齐纳管来替代，它们对噪声的控制是没有作用的。

参考文献：

[1]  R. D. MIDDLEBROOK and S. CUK, A general Unified Approach to Modeling Switching Converter Power Stages , IEEE PESC, Vol.21, No.1, 18-34, 1976. Record, pp 18-34 Vol.35, No.8, 830-839, 2005.
[2]  姜岩峰，谢孟贤。微纳电子器件，北京：化学工业出版社，2005
[3]   R. KELLER, Closed Loop Testing and Computer Analysis Aid Design Of Control Systems , Electronic Design, Vol. 22, No.12, 132-138, 1978.
[4]  V. VORPERIAN, Simplified Analysis of PWM Converters Using The Model of The PWM Switch, Parts I (CCM) and II(DCM) , Transactions on Aerospace and Electronics Systems, Vol. 26, No.3, 21-48, 1990.
[5]   S. SANDLER, SMPS Simulations with SPICE3 , McGraw, 1990
[6]  Sam BEN-YAAKOV, Average Simulation of PWM Converters by Direct Implementation of Behavioral Relationships, IEEE  Applied Power Electronics Conference (APEC’93), pp 510-516