低功耗CMOS电压基准源的设计

　　1 引 言

　　电压基准可以在温度及电源电压变化环境中提供稳定的参考电压，被广泛应用于比较器，A／D，D／A转换器，信号处理器等集成电路中。目前已有不少和工艺的电压基准应用于实际中，并且获得了很高的精度和稳定性。然而随着各种便携式移动通信和计算产品的普及，对电池的需求大大加强，但是电池技术发展相对落后，降低电路的功耗成为IC设计关注的一个焦点；电路的功耗会全部转换成热能，过多的热量会产生焦耳热效应，加剧硅失效，导致可靠性下降，而快速散热的要求又会导致封装和制冷成本提高；同时功耗大将导致温度高，载流子速度饱和，IC速度无法再提升；并且功耗降低，散热减少，也能减少对环境的影响。因此，功耗已成为超大规模集成电路设计中除速度，面积之外需要考虑的第三维度。

　　传统的带隙面积大、功耗大、不适应低功耗小面积的要求。本文立足于低功耗、小面积、利用工作于弱反型区晶体管的特点，对传统的带隙电压基准源做出改进，设计了一款最大消耗380 nA电流的电压基准源，大大减小了面积，且与CMOS工艺兼容，同时提出一种新的不耗电的启动电路。本文先介绍传统典型带隙基准电路的原理与功耗组成，提出改进电路结构，并进行分析，最后给出基于0.5μm CMOS工艺模型的仿真结果和测试结果。

　　2 传统带隙电压基准源

　　传统带隙基准源如图1所示。

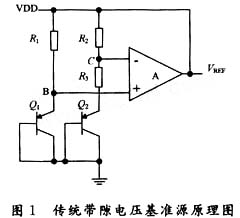
　　由PTAT产生电路，负PTAT产生电路，放大器，加法器组成。原理是由Q1，Q2两个PNP三极管和电阻R3产生PTAT电流，流过电阻R2产生PTAT电压，再叠加上Q2的负PTAT电压Vbe，通过合理调整电阻R2和R3的比例产生与温度无关的电压基准。运算放大器A是为了保证B，C两点电压相等。

　　这种结构需要三极管、运算放大器以及若干电阻，面积比较大。其工作时电流由3部分组成：Q1支路的集电极电流；Q2支路的集电极电路，运算放大器A的工作电流。其中Q1，Q2支路的电流为VTln N／R3，其中VT=kT／q；q是电荷常量；k是波尔滋曼常数；T是绝对温度；N是三极管Q2与Q1的比值，通常为8，同时要达到好的性能运算放大器的电流不能太小以使晶体管工作于饱和区。通常传统带隙电压基准源消耗电流不小于10μA。

　　3 弱反型区晶体管模型

　　本文利用了工作在弱反型区晶体管的特点，对传统带隙电压基准电路进行了改进。工作在弱反型区的晶体管特性模型假设：

　　(1)晶体管沟道长度足够长，沟道长度近似成立，并且沟道长度调制效应可以忽略；

　　(2)空间电荷区的产生电流可以忽略；

　　(3)表面态密度和表面势的波动可以忽略。

　　在这些假设之下，工作在弱反型区的晶体管的I-V特性可以表示为：

　　ID0是特征电流；S是晶体管的宽长比；n是斜率因子；VG，VS，VD分别为晶体管栅、源、漏端与衬底的电压差。当晶体管由相同的VS电压偏置时，斜率因子n是常数，ID0也可以认为是常数。由式(1)可以看出，当VD-VS》0时，弱反型工作的MOS晶体管与三极管的直流传输特性一致。

　　4 电路实现

　　图2为本文改进的电压基准源的原理示意图。电压基准电路由3部分组成：启动电路、PTAT产生电路和输出电路。输出电路包括电流放大和电压叠加。

　　PTAT电路由M6-M13和R1构成，利用其工作在弱反型区晶体管的特点，取代了传统的三极管PTAT产生电路，且不需要运算放大器，面积大大减小，弱反型区晶体管特性令工作功耗大大降低。P型晶体管M6与M7组成第一对电流镜，增益为S7／S6，N型晶体管M12与M13组成第二对电流镜，增益为S12／S13，只要2路电流足够小，电阻R1的影响就可以忽略，2路电流相等。M6～M13组成一个闭合环路，环路的增益为2组电流镜增益的乘积。其中晶体管M6与M7的宽长比要足够大，工作在弱反型区，M12与M13沟道长度要足够长，工作在饱和区。M8，M9和M10，M11分别与M6，M7和M12，M13构成共源共栅结构，增大阻抗，提高基准电压源的电源抑制比。环路的起始增益大于1令两支路的电流增加，直到平衡则增益降为1，电阻R1上的压降为VR1。根据公式(1)，VR1可以表示为：

　　则流过电阻R1的电流为：

　　由式(3)可以看出，电流IR只与晶体管宽长比，电阻R1，斜率因子n；波尔滋曼常数k，绝对温度T有关，与电源电压无关，是与温度成正比的PTAT电流。

　　电压基准输出电路由晶体管M14～M19，以及电阻R2，三极管Q1，电容C2组成。M18与M19镜像PTAT电流同时M15与M17镜像M18，M19支路的PTAT电流，组成电流放大，采用共源共栅结构是为了镜像更准确。PTAT电流流过电阻R2，产生与温度成正比的PTAT电压，此PTAT电压和二极管方式连接的三极管Q1的Vbe电压叠加，产生与温度无关的基准电压，电容C2是为了滤波，降低噪声。

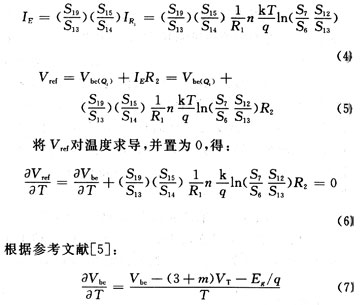
　　其中Eg为硅的带隙能量；m为迁移率的温度系数常数。