基于FPGA的自然对数变换器的设计与实现
实现方法
本文引用地址:http://www.amcfsurvey.com/article/86941.htm · 预处理单元
欲利用CORD IC方法求自然对数,必须对输入进行初始化,经迭代运算后才能得到对数运算值。该对数变换器的输入为16位数,在预处理单元中将输入分别加减一,并将位宽扩大为40位,最高位作为符号位覆值给第一次迭代的x0和y0,如图1所示,图中s代表符号位。扩大位宽可以提高输出精度。
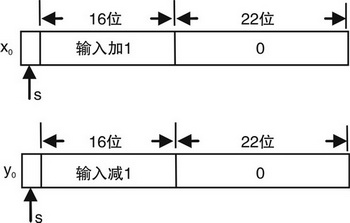
图1初始迭代值x0,y0
· CORD IC单元
CORD IC单元是实现对数变换器的核心。本文利用流水线结构实现CORD IC算法,其结构如图2所示。在设计中,采用由28级CORD IC运算单元组成的流水线结构,为扩大输入范围,从n=-5开始迭代,移位序列为[7,6,5,4,3,2,1,2…28]。前6级根据(3)式进行迭代,后22级根据(4)式进行迭代。经过28级流水线运算后,y变为0,z左移一位就是要求的对数值。每一级电路结构主要包括2个移位寄存器和3个加减法器,这些移位寄存器各自有不同的固定的移位次数,加减法选择由该级中y的最高位(符号位)决定。θn为第n次迭代的旋转角度,并作为常数直接连到了累加器上,不需要存储空间和读取时间。
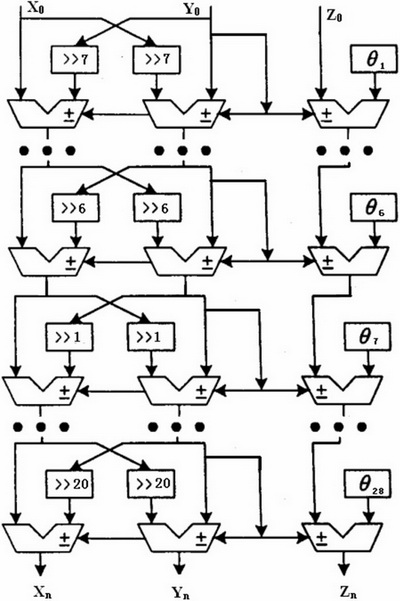
图2 CORDIC流水线结构
· 后处理单元
由CORD IC得到的z=1/2ln(t),因此将结果左移一位,并截取高16位作为最终的输出。其中最高位为符号位,最大输入值65535的对数值为11.0903,对应的输出为7FFF,其余输出均除以对应的值即得到相应的对数值。
实验结果
在Quartus II 5.1软件环境下使用Verilog HDL语言完成了上述各算法,并在cyclone系列芯片EP1C6Q240C8上实现。图3 为对数运算时序仿真图。表1为对数运算结果与理论值的比较。

图3对数运算时序仿真图
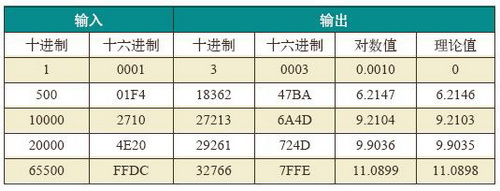
由表1可看出,该对数运算器的输出误差为10-4数量级。由于采用流水线结构,能够在执行进程的同时输入数据,从而极大的提高了程序的运行效率。该设计需要30个时钟周期获取第一个计算结果,而只需要一个时钟周期来获取随后的计算结果。利用Quartus Ⅱ5.1软件进行时序分析,该运算器的最高频率可达到80MHz。该运算器适用于高速大数据量的数据处理。
表1对数运算结果与理论值的比较
结语
利用对数变换可以将乘除法变换为加减法实现,有利于乘除法在硬件中的实现。由于CORD IC算法完全由移位和相加运算完成,降低了复杂性,易于硬件的实现。笔者利用CORD IC算法在FPGA上设计了一种自然对数变换器。实现过程中采用流水线结构,提高了系统的运行效率。实验结果表明该对数运算器的输出误差为10-4数量级,最高频率可达到80MHz。该运算器适用于高速大数据量的数据处理。
参考文献:
1. 李刚、李秋霞、林凌、李小霞等,动态光谱频域提取的FFT变换精度分析,光谱学与光谱分析,2006,12:2177-2180
2. Bajard J C,Muller J M.BKM: A new hardware algorithm for complex elementary functions.IEEE Trans computers,1994,43(8):955-963
3. Hormigo J,Villalba J,Schulte M J.A hardware algorithm for variable precision logarithm[c]//proceedings of the IEEE inter conf on application-specific systems,architectures and processors,2000:215-224
4. Abed K H,Siferd R E. CMOS VLSI implementation of a low power logarithmic converter. IEEE Trans computers,2003,52(11):1421-1433
5. Uwe Meyer-Baese.Digital SignalProcessing with Field Programmable Gate Arrays[M].Tsinghua University Press. 2006:79-87
6. J.S.Walther. A unified algorithm for elementary functions. in proc.Spring Joint Comput.Conf.,1971:379-385
7. Chih-Hsiu Lin and An-Yeu Wu.Mixed-Scaling-Rotation CORDIC(MSR-CORDIC) Algorithm and Architecture for High-Performance Vector Rotational DSP Applications. IEEE Transactions on circuits and systems-I:REGULAR PAPERS, 2005,52(11):2385-2396
8. Xiaobo Hu,Ronald G. Harber,Expanding the range of convergence of the CORDIC algorithm. IEEE Transactions on computers, 1991,40(1):13-21
9. Altera公司,“Cyclone FPGA Family data Sheet”














评论