基于多径分量簇的信号处理技术研究

　　0 引言

　　实际传播场景下，对每个多径分量簇内的不同多径分量加以分别处理将会消耗大量的阵列自由度并占用大量的资源，而其结果所带来的性能增益却是极其有限的，为此，如何对空域多径簇进行恰当的处理，是研究阵列天线自适应信号处理相关算法实现中的一类重要问题。

　　一般认为，移动通信领域中的阵列信号处理技术从其技术复杂度出发至少可以分为3个实现层面：

　　其一，是在基站台采用阵列天线的形式而实现上行链路信号的空间分集处理，这在当前移动通信系统中已经得到普遍应用。

　　其二，是基站台阵列天线波束扫描技术，可以分别进行波束俯仰角和方位角扫描——前者可用于基站天线辐射波束下倾角的电调整，后者则可以实现基站台和移动台无线通信链路的定向传输。

　　其三，即自适应阵列天线处理技术。自适应天线是一种能根据环境变化，通过自行调整对天线阵中各阵元的加权值以改善其输出特性的一类重要的天线技术。它基于使天线阵列输出某一方面的性能指标为最优，而实现天线性能对信号环境的响应。

　　出于上述认识，尝试利用不同的空间信号处理技术，考察将一个来波簇作为单一来波进行处理时所引入的性能差异。

　　1 空间分集技术

　　空间分集技术是利用相距足够远的不同天线产生的电场相互独立这一特性而构成的分集技术，通常，接收天线之间的间隔应足够大，以保证每个接收天线接收到的信号的衰落特性是相互独立的。若空间分集天线接收到的信号为单一来波，且每一路信号衰落到门限电平以下的概率为p，那么L路信号同时衰落到门限电平以下的概率就为pL，当L较大时，显然pL<<p，但是，当空间分集天线接收到的信号为来波多径簇时，由于多径分量簇是由不同特性的来波所组成，因而其输出信号衰落到门限电平以下的概率将会受到多种因素的影响。例如，来波分量在多径簇内的分布、各射线路径之间的相关性以及阵列处理性能如采样快拍数等。这就使得L路输出信号同时衰落到门限电平以下的概率呈现出某种动态变化的特征，也就是说，如果一个分集支路的簇信号为深度哀落，而另一个分集支路的簇信号较强，若强信号簇之路径功率大于弱信号簇支路功率，则总输出信号就可能不会衰落到门限电平以下。

　　为了进一步得到确切的关系，在此以两分支空间分集接收天线为例，分别计算来波簇和单一来波情形下的空间分集增益。选择的仿真参数为：每天线来波簇个数N=2，来波簇平均来波角φ1=-φ2，取值为30°和60°，来波簇角扩展△1=△2=10°，簇内来波角概率密度函数服从均匀分布，每天线的阵元数n=10，合并方式为最大比合并，中断率Pout=10-2。利用蒙特卡罗仿真方法可得2种情形下的分集增益与天线间距的关系，在单一来波情形下的分集增益随分集间距的增加平坦增加，而来波簇情形下的分集增益随分集间距的增加呈现出振荡增加的特征，且来波簇的平均来波角越大，振荡特性就越明显，但是，来波簇情形下的最大分集增益与单一来波情形下的最大分集增益基本相同，这与实测的结果相吻合。

　　2 波束扫描技术

　　基于以上的分析，尝试用波束扫描技术号察将一个来波簇内的信号作为单一来波信号加以处理时，所引入的来波方向估计结果误差。由文献[3]可知，该误差受到多种因素的影响。例如，多径簇内来波分量的分布，来波簇入射中心角、来波簇角域范围、来波簇内射线相关性以及阵列处理性能如采样快拍数等。在此以全向阵元构成的三元均匀直线阵模型为例，利用数值分析，来分别考察连续采样和离散采样情况下各种因素不同影响下，由2个自相关矩阵差异所引入的来波方向估计结果的变化。其中，阵列输出数据矢量的各分量问具有线性的相位关系，在计算中，选择阵元间距d为0.5λ，λ为工作波长。

　　(1)来波多径簇角域范围内射线相关性对误差的影响

　　选取的仿真参数为：多径簇来波中心角度为30°，角域范围为10°，在角域范围内随机等概地确定各方向入射射线数目(n=10，20，30，40，50，80，100，200)，每根射线的幅值服从均值为0，方差为1的复高斯分布，且多径簇内任2根射线间的相关系数依次服从模值为0，0.2，0.3，相位在区间[0，2π]内均匀分布。对阵列输出进行连续采样以得到阵列输出自相关矩阵，通过特征分解，可以基于数值计算来进一步分析。

　　在图1所给出的结果中，为得到统计平均结果，已分别进行了500次独立计算。

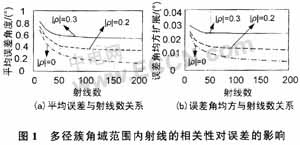
　　图中结果表明，随着来波多径簇内射线数目的增加，来波方向估计误差是逐渐减小的，然而，在射线数目相同时，随着多径来波簇内射线相关性的增强，来波方向估计误差变大，需要更少的射线就能使得来波方向估计误差收敛。

　　(2)来波多径簇角域范围对误差的影响

　　选取的仿真参数为：多径簇来波中心角度为30°，角域范围为5°和10°，每个簇内射线的数目为50根且服从均匀分布，每根射线的幅值服从均值为0，方差为1的复高斯分布，射线相关系数服从幅值为0.3，相位在[0，2π]内均匀分布。图2中给出一组数值计算结果。

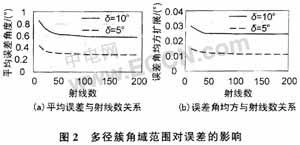
　　图中结果表明，随着多径簇角域范围的增大，对多径簇中心角的估计误差随之而增大。

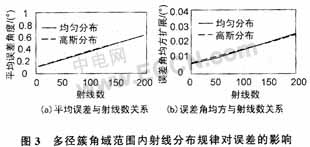
　　(3)来波多径簇角域范围内射线分布规律对误差的影响

　　选取的仿真参数为：多径簇来波中心角为30°，角域范围在2°～10°范围内取值，射线分布规律为均匀分布和高斯分布，每个簇内射线的数目为50根，每根射线的幅值服从均值为0，方差为1的复高斯分布，射线相关系数服从幅值为0.3，相位在[0，2π]内均匀分布。图3中给出一组数值计算结果。

　　图3中结果表明，多径簇内来波入射角不同的分布规律对多径簇中心角估计误差的影响不大。

　　(4)来波多径簇中心角度对误差的影响

　　选取的仿真参数为：多径簇来波中心角为10°和30°，角域范围为10°，每个簇内射线的数目为50根且服从均匀分布，每根射线的幅值服从均值为0，方差为1的复高斯分布，射线市H关系数服从幅值为0.3，相位在[0，2π]内均匀分布。利用上文的仿真方法，其仿真结果表明，多径簇的中心角度不同时，多径簇中心角估计误篾会也随着变化。

　　(5)采样快拍数对误差的影响

　　选取的仿真参数为：多径簇来波中心角为30°，角域范围为10°、20°、30°，快拍数为10、20、30、40、50、80、100，每个簇内射线的数日为50根且服从均匀分布，每根射线的幅值服从均值为0，方差为1的复高斯分布，射线相关系数服从幅值为0.3，相位在[0，2π]内均匀分布。利用上文的仿真方法，其仿真结果表明，随着快拍数的增大，来波多径簇中心角度的估计误差呈现出不断减小的规律。

　　综合以上分析可以看出：

　　①将来波多径簇作为单一来波处理，可以得到一个视在来波角度，这一角度和实际多径来波簇的中心角度存在一定偏差；

　　②随着多径来波簇内射线数目的增大，视在来波角度和实际多径簇中心角度的误差快速减小。这一效果同样出现在增大阵列输出采样快拍数的情形下。考虑到二者都是以更多的样本数目来实现阵列输出结果趋近于真实结果，这表明，增加处理样本的数量可以得到对来波中心角度的更准确的估计；

　　③相同来波簇中心角度和角域范围下，随着来波簇角域范围内射线相关性的增强，误差角度随之而增大，且误差收敛所需射线数目也随之减少；

　　④多径簇内来波入射方向的分布规律没有对视在来波角度和实际多径簇中心角度误差产生明显影响；

　　⑤不同来波簇中心角度下，随着来波簇角域范围的增大，误差角度随之而快速增大。

　　⑥对误差角度均方扩展的数值计算结果表明，该指标同误差角度的变化表现出相同的规律。

　　3 自适应天线技术

　　事实上，移动通信环境是随机变化的，从而导致来波角在不断的改变，另外，相干干扰、多径、噪声的存在，使得每个到达阵列的信号参数都在随机变化，恒加权的波束扫描无法自动改变波束方向以适应信号环境的变化，从而可能导致阵列输出中有用信号被干扰信号掩盖。要降低干扰的影响，最好的方法是使其天线方向图零点位置始终指向干扰方向，同时保持主瓣对准所需信号的来波方向。然而，干扰信号和有用信号的来向都是未知的，这就要求天线方向图能自动地改变，换句话说，天线方向性必须具有自适应能力。通常，自适应阵列的输出是对各阵元的接收信号向量X(n)在各阵元分量上的加权和，令权向量W=[w1，w2，…，wM]，即输出可写作：

　　可见自适应天线通过改变式(1)的权向量，便能对来自不同方向的来波多径簇做出不同的响应，从而形成不同方向的空间波束。目前，波束形成的自适应算法主要有以下6种：①最小方差无畸变响应MVDR；②采样数据协方差矩阵求逆SMI；③最陡梯度法SDM；④最小均方误差法LMS；⑤递归最小二乘法RLS；⑥恒模算法CMA。通过选用不同的波束形成算法，便可得到不同的输出信噪比。

　　4 结束语

　　本文利用不同的空间信号处理技术，考察将一个来波簇作为单一来波进行处理时所表现出来的现象及规律，该分析结果将为实际移动通信系统中的空时信号处理技术提供重要的参考，基于本文的仿真结果，将为研究阵列天线自适应信号处理的相关算法提供有益的帮助。