RBF神经网络在红外CO2传感器压力补偿中的应用研究
0 引 言
本文引用地址:http://www.amcfsurvey.com/article/82979.htm在目前种类繁多的CO2传感器中,红外光学式因为其体积小、寿命长、反应快、精度高等优点,已经成为CO2气体分析最常用的方法,但因环境总压的影响一直是这种分析方法中难以解决的主要问题之一,所以,它的适用范围受到了很大的限制。在实际应用中,此类传感器通常都用在标准大气压环境中,其环境总压基本保持恒定,不存在受总压影响的情况。目前,一些精度较高的红外CO2传感器都通过采用压力补偿措施来保证分析测量精度,其中,比较简单常见的一种数学方法是利用最小二乘法对不同分压值的CO2气体由于环境总压变化引起的测量误差进行直线、指数或者多项式拟合。这种补偿算法在环境总压小范围变化的应用中取得了良好的效果,但误差会随着测量的CO2气体分压值的增高而变大,并且,当环境总压变化范围较大后,补偿的效果将会很差。
本文提出构建径向基函数(radial basis function,RBF)神经网络模型,将其作为压力补偿方法应用于红外CO2传感器来预测CO2气体分压值,期望能有效地解决在环境总压大范围变化情况下精度差的问题。
1 红外CO2传感器结构与原理
红外CO2传感器的设计利用红外吸收原理,其吸收关系服从Lambert-beer定律
![]()
式中,I0为入射光强;I为出射光强;c为单位面积上分子数的线密度;l为红外光透射的空间长度;u为吸收系数,它与环境压力、温度、气体的种类、入射光的光谱波长等因素有关系。
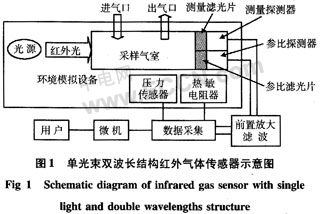
本文实验所用红外CO2传感器为单光束双波长结构,如图1所示。选用1个红外光源,2只探测器,将光源和探测器分别安装在一只采样气室的两端。其中,一只探测器前安装能透过4.26μm波长红外光的滤光片,CO2气体可吸收4.26μm波长的红外光,因此,可用于探测CO2信号U1,形成测量光路;另一只探测器前安装透过4μm波长红外光的滤光片,CO2气体不吸收4μm波长的红外光,因此,可作为探测CO2信号的参比信号U0,形成参比光路,测量信号与参比信号相除可得一比值
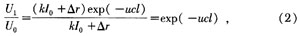
式中k为光能转换为电信号的系数;△r为环境干扰信号,由式(2)可以看出:有效信号只剩下与气体吸收能力有关的参量,与传感器系统的部件性能无关,这样,就可以消除光源辐射强度变化、光学元件污染以及探测器漂移等影响,本文将用这个比值作为传感器的输出信号。另外,传感器中内置热敏电阻器,用于输出温度信号,环境压力通过压力传感器测得。对传感器进行的压力补偿分析即是研究在输出温度信号恒定的前提下,传感器输出的比值信号在环境总压取不同值时与要测量的CO2气体分压值之间的映射关系。
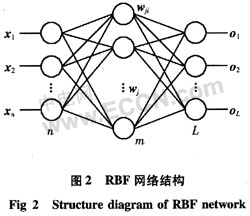
2 RBF网络模型设计
RBF网络属于前馈式网络(feed forward network),通过系统输入与输出所组成的资料来建立分析模型,并借由收敛法则来达成学习之目的。它是一种局部逼近网络,能以任意精度逼近任一连续函数,其结构如图2所示。RBF网络由三层组成,隐含层节点由高斯激活函数构成,隐含层第j个节点的输出可表示为

式(4)针对红外CO2传感器压力补偿模型而言,CO2气体分压值与传感器输出比值信号存在对应关系,在加入总压影响这个因素后,实际上就形成了一个二对一的结构,所以,这里输入样本表示为x=(x1,x2)T,其中,x1表示传感器输出比值信号,x2表示总压值,L是输出层节点数,取1,表示需预测的CO2气体分压值,wkj,cj,σj为网络参数,m是隐含层节点数,在之后网络训练的过程中通过实验法确定为14
2.2 样本数据获取与预处理
在选定了网络的输入和输出模式后,需获取一定量的覆盖较全面的样本数据来对网络进行训练和测试。获取过程采用固定CO2分压逐点加总压的方法进行,总压范围为30~110 kPa,每5 kPa一个点,全部实验是在恒定温度(27℃)下进行。经过实验,可获得187组样本数据,分别选取各CO2分压值点中的其中一个压力点的数据组成测试样本,共11组,剩下的176组数据组成训练样本。为了使这些数据对于网络更容易训练和学习,需进行尺度变化将它们变化到[0,1]区间内。
2.3 网络算法
根据尺度变化后的样本数据,网络算法可分以下几步进行:
1)选取网络的中心向量cj和标准化常数σj。这里,采用k-均值聚类法求解,它能准确计算出这2个参数的最佳初始值,与通常采用的设初始值为随机值的方法相比,这种算法非常有效地加快了网络的收敛速度。
2)求解网络模型的初始权值wkj。隐含层节点有14个,在聚类法求出初始中心向量和标准化常数后,对于176组训练样本,可以推论输出矩阵为

通过式(5)求出网络的最佳初始权值,对加快网络收敛速度也起了相当大的作用。
3)经过(1),(2)步的求解,网络模型初始参数已确定,在网络传递过程中,利用最陡坡降法通过误差函数来反馈修正隐含层和输出层的参数,误差函数用系统总误差表示为
![]()
式中p为训练样本数,取176;ti,yi分别为在样本i的作用下输出节点的期望输出和实际输出。第n+1次训练后的系数相对于第n次训练后的系数修正公式为
![]()
式中n为训练次数;η为学习速率,取值为0.001;Z=wj,cj,σj。
4)经过不断正向传播,反向修正,求得网络的最终参数,再用测试样本数据检验网络性能。
2.4网络模型结果分析
利用MATLAB工具强大的数值矩阵运算和绘图功能,整个网络算法是通过编写M文件进行编译完成。在用测试样本数据检验时,保持网络参数不变,正向运行该网络,每训练一次,即用测试数据测试一遍,其均方误差随训练次数变化的曲线如图3。
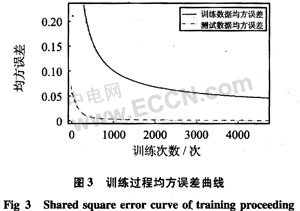
从误差曲线可以看出:在用测试数据检验时,均方误差开始减小,随着训练次数的增加慢慢趋于平衡。选择训练次数的原则是:选择尽量少的训练次数以取得尽量小的测试均方误差,使网络具备很好的泛化能力。这里,取训练次数为50 000次,训练时间约为4 min,训练均方误差可到0.028 1,测试均方误差可达到0.001 527。网络的最佳结构取14个隐含层节点,这里,通过实验法比较取不同隐层节点数后的均方误差来确定。
图4为网络模型对训练样本的预测值与实际值的比较,图5为网络模型对测试样本的预测值与实际值的比较。
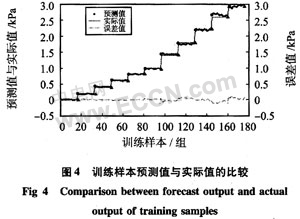
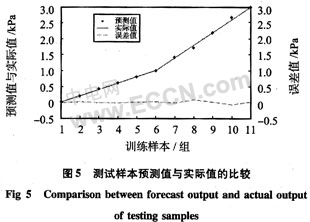
由图4看出:网络模型对训练样本的预测值同实际输出基本相符,平均误差为0.038 kPa,精度可达1.26%,误差最大值为0.12 kPa;由图5看出,网络模型对未经训练的测试样本的也可给出准确的预测值,这个预测值与实际输出值的平均误差为0.035 kPa,精度可达1.18%,误差最大值为0.079 kPa;测试数据结果分析证明:该网络模型具有非常好的泛化能力,而且,解决了CO2气体分压值较高时精度差的问题。
3 结论
综合以上分析与比较可以看出:在环境压力变化范围较大的情况下,将神经网络应用于构建压力补偿模型,通过采集传感器的输出比值信号和压力信号来组成样本并进行分类和预处理,然后,用基于k-均值聚类和最陡坡降法的RBF网络依据样本来建立输入变量和输出变量之间的映射关系,以预测被测气体所含CO2气体分压值。该网络模型使用实验法确定网络的最佳结构,在网络初始参数选取上做了较细的处理,故具有很快的收敛速度。实验结果表明:这种算法模型收到了良好的效果。可以预见,神经网络将发展成为预测传感器在复杂环境中的输出信号的一种可行的有效的工具。









评论