数字形态学滤波器与智能车路径记忆
引言
本文引用地址:http://www.amcfsurvey.com/article/81348.htm “飞思卡尔”杯全国大学生智能车竞赛规则明确指出,智能车在赛道上连续跑两圈,并记录其中最好的单圈成绩,这使路径记忆算法成为可能。如图1所示,赛道记忆算法在第一圈以最安全的速度缓慢驶过一圈,并将赛道信息保存下来,第二圈根据保存下来的信息进行车速和转角决策的相应最优化,从而在第二圈取得好成绩。无论智能车的传感器前瞻距离有多远,在跑圈时它都只能预测在一段有限距离内赛道的情况。而采用赛道记忆算法的智能车,在第二圈时已对整个赛道有了全面的认识,从而在相同条件下,将比不使用赛道记忆的智能车更具优势。
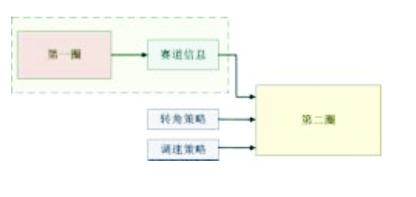
第一圈准确记忆赛道信息是第二圈控制策略的基础,是比赛成败的关键。但是在第一圈中不论控制策略如何优秀,赛车总会或多或少的偏离赛道,舵机的转角信息总会出现一定程度的毛刺和扰动等粗大误差,其幅值足以引起处理器的误判。如果不加处理直接应用于第二圈控制,会对赛车造成严重干扰,不能以极限速度跑完比赛或者冲出赛道。通常的处理方法有两种:一是通过阈值比较丢弃干扰值,但同时赛道信息也会同干扰信息一起被丢弃;二是通过低通滤波将干扰平均到多个位置,但同时破坏了赛道原始信息,而且在干扰幅值很大的时候效果也不是很明显。
数学形态学(Mathematical Morphology)是一种新型的数字图像处理方法和理论,其主要内容是设计一整套的变换(运算)、概念和算法,用以描述图像的基本特征。提供了非常有效的非线性滤波技术,该技术只取决于信号的局部形状特征。因此,它在诸如形状分析、模式识别、视觉校验、计算机视觉等方面,要比传统的线性滤波更为有效。
算法的选取与实验结果对比
数学形态学的运算以腐蚀和膨胀这两种基本运算为基础,引出了其它几个常用的数学形态运算。数学形态学中最常见的基本运算只有七种,分别为:腐蚀、膨胀、开运算、闭运算、击中、细化和粗化,它们是全部形态学的基础。它们的定义如下:
设X代表一个数字图像,我们假定该图像是二值的,即取值只有1或0,则X表示一个二进制信号集合,B是一个简单的紧集合,称为“结构元素”。X被B膨胀和腐蚀的结果可以分别定义为:
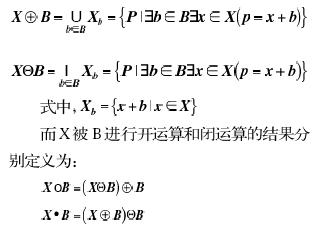
在数字图形处理领域中,数学形态学主要用于非线性变形,它可以局部地修改信号的几何特征,并提供有关信号的几何特征信息。根据不同的信号的形态特征,可以采用不同的数学形态学运算对信号进行处理,这些数学形态与运算都被视为数学形态滤波器。在这种应用方法中,每一个信号都被视为适当的维数的欧几里德空间中的集合。数学形态滤波器被定义为集合的运算,它使信号的图形变形,以提供关于其几何结构的数字化信息。对于被视为集合的二进制信号,腐蚀、膨胀、开运算和闭运算是最简单的形态运算。这些滤波器还可以引申到多维信号中去。此时,形态滤波器利用的是灰值图的数学形态运算的定义。下面将探讨如何将数学形态滤波器应用到舵机转角信号(一维数字信号)的处理中,实现去除脉冲噪声和减小扰动,以及在单片机上编程实现和快速运算的方法。
数学形态滤波器通常是用在二维图形的处理,为把数学形态滤波器推广到一维的信号的处理中,下面再介绍一下腐蚀、膨胀、开运算和闭运算这一个基本运算在一维信号处理中的定义:
设H、K分别为h[n]和k[n]的定义域,长度分别为N和M,一般N>M。H和K均为整数集合。
h[n]指包含舵机转角信号的数字化序列,k[n]指结构元素序列。
h被k腐蚀:
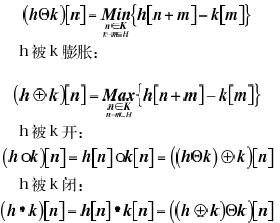
采用数字形态滤波方法,还要选用合理的算法。其中,如何选取模板序列的长度是关键,如果模板序列过长会将有用信号当作噪声滤除,过短则达不到滤除噪声的目的。在采样速率一定的情况下,序列的长度与时间成正比,这要求模板的长度要小于模型车的最小转弯时间,大于舵机扰动的最长时间。第一圈让模型车匀速通过,这样处理有两个优点:
1) 可以固定最小转弯时间,从而确定模板的长度。非匀速通过时速转弯时间不定,要求模板长度可变,从而造成后续处理复杂,稳定性不高。
2) 采样序列的顺序可以直接转化为位移量,便于后续控制策略处理。相对于非匀速通过速度与时间乘积得到的位移,直接转化得到的位移更准确(在标准的韩国赛道上,实验模型车直接转化得到的赛道长度误差小于5cm,速度与时间乘积得到赛道长度误差在10cm以上)。
实验系统在图2所示的赛道上,智能车对赛道信息的采样速率为200Hz,以1.5m/s的速度匀速跑完第一圈的数据如图3所示。可以看到在弯道中,舵机的转角信息存在着严重的毛刺和扰动,不能直接用于第二圈的控制策略。图4为matlab中采用3阶巴特沃兹滤波处理后的结果,干扰的抑制效果仍然不理想,而且运算量偏大,单片机难以承受。图5为采用形态学滤波处理后的数据,赛道信息完整准确,可以较好的应用于后续控制策略。

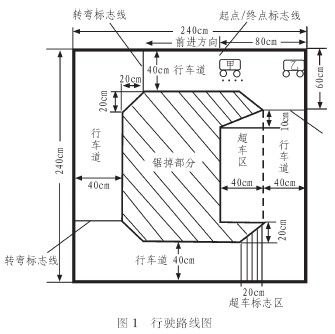
图2 实验系统采用的赛道
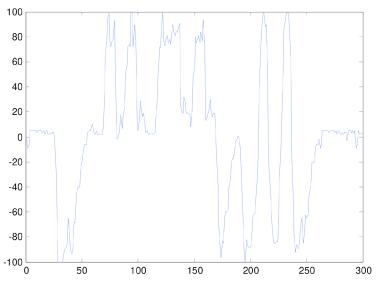
图3 第一圈记录的赛道信息
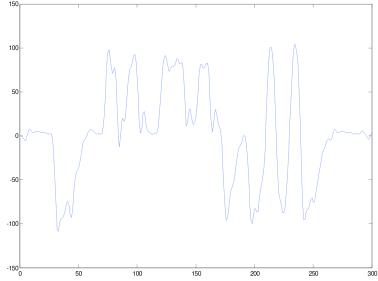
图 4 3阶巴特沃兹滤波器处理后数据
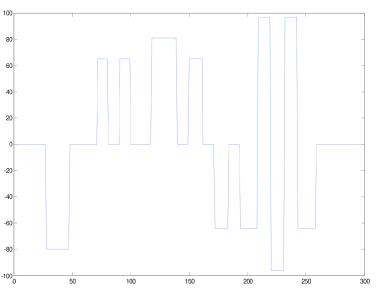
图5 形态学滤波处理后的数据
数学形态滤波的快速算法
由于数学形态滤波器只由加法、减法和比较运算构成,其运算相对简单,因此,它很适合于在计算功能相对较弱的单片机上应用并能取得很好的效果。以往单片机由于受存储容量、计算速度及字长的限制而使大多数的数字滤波器较难实现,而形态滤波器则为单片机应用数字滤波器代替以往的模拟滤波器提供了一条新的途径。
由腐蚀的定义可知,欲计算f(n)的腐蚀值,需要知道该点前w(w为结构元素的宽度)点的数据;而要计算f(n)膨胀后的结果,则需要知道该点后w点的数据。由于运算是一个腐蚀运算接着一个膨胀运算后得到的,在长度为L的数据中只有从第w点到第(L-w+1)点,才可以得到开运算的结果。
如图6所示,我们定义一个模板序列,该序列的长度和结构元素的宽度相同。该模板的初始值由前w个点的腐蚀值组成。以第n点为例,沿该点向前的方向对模板序列的值进行膨胀运算,运算的结果即为该点的开运算的结果。同时,沿该点向后的方向继续进行腐蚀运算,得到第(n+1)点的腐蚀值。将(n+1)点的腐蚀值作为模板序列的最后一个点,并将模板序列前(w-1)点顺次向前移动一个位置。更新后的模板值即可用来做 (n+1)点的膨胀运算,得到在(n+1)点的开运算值。如此继续下去,就可完成全部的开运算。在做闭运算也可采用类似的方法来提高计算的速度。

图6 数学形态滤波快速算法
这样,对长度为N的一段数据,用M个零作为其结构元素进行处理时,当采用一般方法进行计算,需要进行2×M×N次的比较运算。而当采用快速算法时,能够在比较最大值的同时得到最小值,减少(N-M+1)×M次比较运算,使程序的执行速度提高了近一倍,而且,由于采用这种快速算法,可以实现路径记忆信息的实时处理,很大程度上方便了第二圈控制策略的制定,因此,它使得形态滤波这种方法更加适合应用于路径信息的处理中。
实验及结论
通过对不同传感器方案(光电管和CCD)的智能车在不同赛道多次实验发现,对于光电管方案和CCD方案的智能车,赛道记忆算法都能一定程度上提高第二圈速度。智能车采用形态学滤波算法处理赛道记忆数据后,不但行驶的稳定性、准确性有了较大的提升,而且没有大幅增加MCU的资源消耗,同时可以支持复杂的控制策略。上述方案具有很强的通用性,适用于不同传感器方案、不同控制算法的智能车。






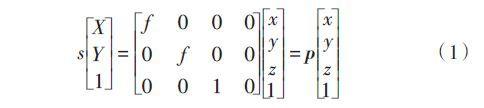








评论