基于Matlab的数字滤波器的设计与应用研究
1 引 言
本文引用地址:http://www.amcfsurvey.com/article/81005.htm数字滤波器是数字信号处理的基础,用来对信号进行过滤、检测与参数估计等处理,在通信、图像、语音、雷达等许多领域都有着十分广泛的应用。尤其在图像处理、数据压缩等方面取得了令人瞩目的进展和成就。鉴于此,数字滤波器的设计就显得尤为重要。
目前数字滤波器的设计有许多现成的高级语言设计程序,但他们都存在设计效率较低,不具有可视图形,不便于修改参数等缺点,而Matlab为数字滤波的研究和应用提供了一个直观、高效、便捷的利器。他以矩阵运算为基础,把计算、可视化、程序设计融合到了一个交互式的工作环境中。尤其是Matlab工具箱使各个领域的研究人员可以直观方便地进行科学研究与工程应用。其中的信号处理工具箱、图像处理工具箱、小波工具箱等更是为数字滤波研究的蓬勃发展提供了可能。
本文主要介绍基于Matlab环境的IIR数字滤波器的设计,然后将设计结果应用于图像处理,针对处理结果进一步分析了滤波器性能的优劣。
2 IIR数字滤波器的设计
IIR数字滤波器最大的优点是给定一组指标时,他的阶数要比相同组的FIR滤波器的低得多。基于Matlab的IIR滤波器的设计方法主要有完全设计法、模拟原型设计法和直接设计法等。
2.1 模拟原型法
采用经典低通滤波器作为连续域上的设计模型,通过频域变换得到IIR数字滤波器,最后还要进行离散化处理。Matlab提供的低通模拟滤波器原型函数包括:besselap,buttap,cheb1lp,cheb2ap,ellipap;频域变换函数包括:lp2bp,lp2bs,lp2hp,lp2lp;离散化处理函数有bilinear和impinvar。
2.2 完全设计法
Matlab信号处理工具箱提供了几个直接设计IIR数字滤波器的函数,直接调用就可以设计滤波器,这为设计通用滤波器提供了方便。
设计Butterworth滤波器用函数butter(),可以设计低通、高通、带通和带阻的数字和模拟滤波器,其特性是通带内的幅度响应最大限度的平滑,但损失了截止频率处的下降斜度。
设计Chebyshev I型滤波器用函数chebyl()。可以设计低通、高通、带通和带阻的数字和模拟ChebyshevI型滤披器,其通带内为等波纹,阻带内为单调。Chebyshev I型滤波器的下降斜度比II型大,但其代价是通带内波纹较大。
设计Chebyshev II型滤波器用函数cheby2()。可以设计低通、高通、带通和带阻的数字和模拟Chebyshev II型滤波器,其通带内为单调,阻带内等波纹。Chebyshev II型滤波器的下降斜度比I型小,但其阻带内波纹较大。
设计椭圆滤波器用函数ellip(),与cheby1,cheby2类似,可以设计低通、高通、带通和带阻的数字和模拟滤波器。与Butterworth和chebyshev滤波器相比,ellip函数可以得到下降斜度更大的滤波器,得到通带和阻带均为等波纹。一般情况下,椭圆滤波器能以最低的阶实现指定的性能指标。
2.3 直接设计法
直接设计方法的思想是基于给定的滤波器参数直接在离散域上寻找合适的数字滤波器,他不限于常规的滤波器类型,如低通、高通、带通和带阻等。这种方法甚至可以设计多带的频率响应,Matlab提供yulewalk函数用于辅助设计。
2.4 通用Butterworth设计方法
使用这种方法设计的Butterworth数字滤波器可以有不同数目的零点和极点,Matlab提供的maxflat函数实现了这一功能。这个函数与butter函数很相似,但他可以指定两个阶参数,其中归一化和非归一化各一个。如果这两个参数的值相同,那么他与butter函数的结果就是相同的。
2.5 参数建模法
寻找接近于所需要设计的滤波器的通用模型,时域上的建模函数为lpc,prony,Stmcb;频域上的建模函数有invfreqs和invfreqz。
3 IIR数字滤波器的实现
当从设计中求得了滤波器H(z)的分子分母系数向量之后,用filter指令可以实现对应的数字滤波器;也可通过Simulink建模仿真来实现滤波器。

(1)用filter指令实现

(2)用Simulink实现
首先构建Simulink模型:

然后设置仿真参数:仿真时间段为0~1 s,求解器采用固定步长的离散求解器,其余参数采用默认值。设置离散滤波器参数:分子系数向量[0,1],分母系数向量[1,-0.8],采样时间0.1 s。
再设置数据输入输出模块的参数,输入变量名为simin,并允许数据外插。输出数据为simout,设定为向量格式,将设置好的仿真存盘为discretfilter.mdl文件。仿真程序:

(3)理论计算

由此可见,用filter指令和Simulink建模仿真结果与理论计算结果是一致的。
4 数字滤波器应用于图像处理
示例:用同一指标的低通滤波器对加不同噪声的同一幅图像滤波效果的比较。
由滤波效果图发现,我们设计的3阶butterworthz低通滤波器在d0(截止频率)为20时。对3种噪声的滤除效果相差不多,都达到了滤除噪声的目的,但使图像均不同程度的模糊。这是因为在一幅图像中,图像的边缘、图像中的颗粒噪声均代表了图像信号的高频分量,而图像的背景则代表了其低频分量。用滤波的方法滤除其商频分最就能去掉噪声,但同时使图像的高频分量得到衰减,也就是说滤波后图像变模糊了。当然也不难想象,Butterworth低通滤波器的截止频率越低,图像信号的高频分量损失就越多,滤波后的图像也就越模糊。
图3使用的是同一阶数(N=5)不同截止频率的滤波器对加入盐椒噪声的图像的滤波效果比较。


5 结 语
综上所述,利用Matlab的信号处理工具箱能够方便快捷地设计和实现各种滤波器,这对于信号的传输和处理有着极其重要的作用。
低通滤波器相关文章:低通滤波器原理
电源滤波器相关文章:电源滤波器原理
高通滤波器相关文章:高通滤波器原理 数字滤波器相关文章:数字滤波器原理




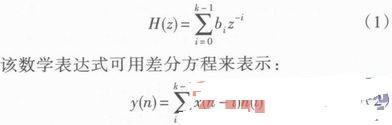



评论