加法器

　　在数字电路中，常需要进行加、减、乘、除等算术运算，而乘、除和减法运算均可变换为加法运算，故加法运算电路应用十分广泛。

1.半加器

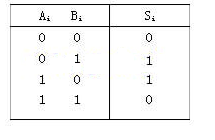
　　不考虑由低位来的进位，只有本位两个数相加，称为半加器。图1(a)为半加器的方框图。其中：A、B分别为被加数与加数，作为电路的输入端；S为两数相加产生的本位和，它和两数相加产生的向高位的进位C一起作为电路的输出。

图1 半加器框图、逻辑图和符号

　　根据二进制数相加的原则，得到半加器的真值表如表1所列。

表1  半加器的真值表

　　由真值表可分别写出和数S，进位数C的逻辑函数表达式为：

                                    （1）

                  C=AB                                   (2)

　　由此可见，式(1)是一个异或逻辑关系，可用一个异或门来实现；式(2)可用一个与门实现。其逻辑电路如图1(b)所示。{{分页}}

2.全加器

　　除本位两个数相加外，还要加上从低位来的进位数，称为全加器。图2为全加器的方框图。被加数A_i、加数B_i从低位向本位进位C_i-1作为电路的输入，全加和S_i与向高位的进位C_i作为电路的输出。能实现全加运算功能的电路称为全加电路。全加器的逻辑功能真值表如表2中所列。

表2 全加器逻辑功能真值表

图2  全加器方框图

　　根据表2可以写S_i和C_i的表达式。经过化简得到最简式：

    由异或门和与非门组成的一位全加器的逻辑图如图3(a)所示。其逻辑符号如图3(b)所示。{{分页}}

图3  全加器逻辑图和符号

　　多位全加器连接可以是逐位进位，也可以是超前进位。逐位进位也称串行进位，其逻辑电路简单，但速度也较低。图4为四位逐位进位全加器。

图4  四位逐位进位全加器