基于SOPC的高精度超声波雷达测距系统设计

摘要：本文基于NIOS II软核处理器和卡尔曼滤波算法，利用FPGA平台，超声波传感器和LCD液晶显示系统，设计了一种高精度超声波雷达测距系统。以这种方法设计的SOPC系统，克服了传统超声波雷达测距系统噪声干扰过大的问题，提高了测距系统的测量精度。

引言

　　传统的超声波雷达测距系统面临噪声过大、测量精度不够高的问题，卡尔曼滤波算法是一种最优化自回归数据处理算法，在雷达测距和目标跟踪等领域有广泛应用，可以用来提高测距系统的精度。但是卡尔曼滤波算法的实现需要用到大量的浮点数矩阵运算，软件实现方式通常很难满足系统对于高实时性的要求，硬件虽然可以保证系统的高实时性，但是硬件无法直接处理浮点数，并且硬件开发周期过长，成本过高，这都限制了卡尔曼滤波算法的应用。

　　NIOS II处理器是可编程逻辑器件的软核处理器，可以和存储器、I/O接口等外设嵌入到FPGA中，组成一个灵活、高效的可编程单芯片系统(SOPC)，大大降低了系统的成本、体积和功耗，适合网络、电信、数据通信、嵌入式和消费市场等各种嵌入式应用场合^[1-3]。

　　本文基于FPGA平台，采用NIOS II软核处理器，利用卡尔曼滤波算法对系统测量值进行滤波处理，设计了一种SOPC系统，以这种方法设计的测距系统综合利用了软件编程灵活的优点以及硬件并行处理、速度较快的特点，运用软硬件协同设计方法保证系统的整体性能最优^[4]，从而大大提高了测距系统的性能和精度。

1 卡尔曼滤波理论

　　对于卡尔曼滤波器，首先我们需要引入一个系统方程：

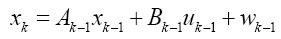
　　系统的测量方程为：

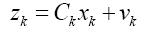
　　对于系统方程，矩阵A称为转换矩阵，矩阵B称为控制矩阵，矩阵C称为测量矩阵，u是控制量，A、B、C、u由实际滤波模型决定，均为已知，上述参数可以是恒定的，也可以是随时间变化的^[5]。w是系统噪声，v是测量噪声。

　　卡尔曼滤波算法由五条滤波公式组成：

　　公式一：状态预测方程

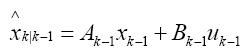
　　公式二：误差预测方程

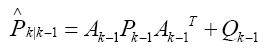
　　公式三：卡尔曼增益方程

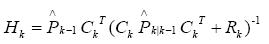
　　公式四：滤波估计方程

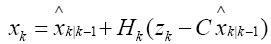
　　公式五：误差更新方程

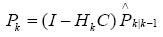
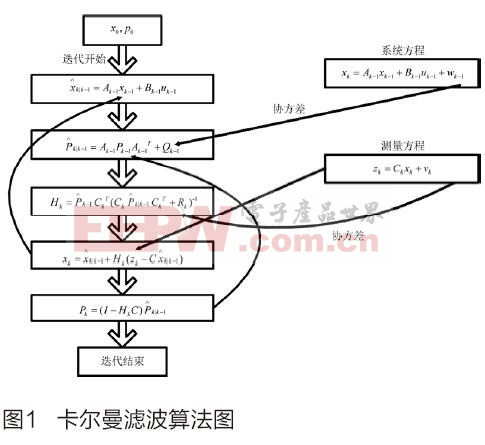
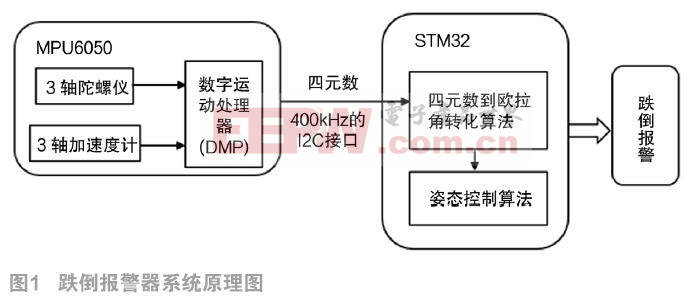
　　卡尔曼滤波算法如图1所示。滤波算法用反馈控制的方法估计过程状态，滤波器首先预测过程某一时刻的状态，然后通过测量值对预测值进行反馈和校正，其中公式一和公式二组成预测方程，产生先验估计，公式三、公式四和公式五组成校正方程，将先验估计和测量值结合构造改进的后验估计，即用测量值对预测值进行校正，卡尔曼滤波器就是通过这样一个不断的“预测(先验)—测量—校正(后验)”的过程，使得最优估计的误差随时间以指数衰减，从而使得数据逐渐“收敛”，以此来达滤波的目的^[6 。

2 系统硬件设计

　　如图2所示，系统的硬件部分由超声波传感器，FPGA开发板以及LCD液晶屏组成。系统工作时，FPGA通过超声波传感器的驱动模块来读取传感器采集的实时测量数据，这些数据经过卡尔曼滤波算法进行滤波和去噪处理后，再通过LCD驱动模块控制LCD液晶屏进行数据的实时展示。

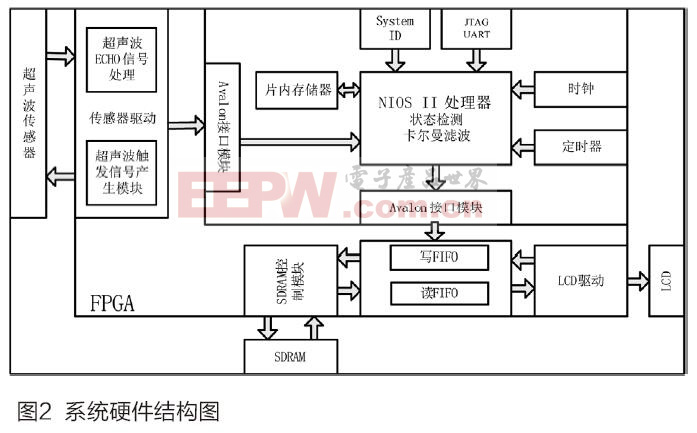
　　在该系统中，超声波传感器驱动和LCD驱动采用Verilog HDL设计，卡尔曼滤波模块通过NIOS II软核中的C语言实现。这样既可以发挥硬件处理速度快的特点，又可以很好的发挥C语言处理浮点数运算和编程灵活的特点，从而保证系统性能最优。

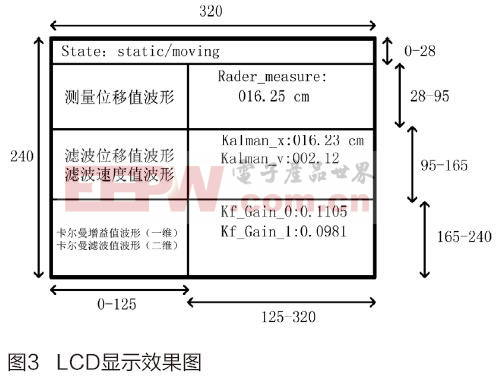
　　系统采用的LCD液晶屏的尺寸是320*240。图3是LCD屏幕的分区显示效果图，液晶屏最上部显示运动状态检测结果，下部显示实时数据，其中左侧显示实时波形曲线，右侧显示实时数值数据。

3 系统软件设计

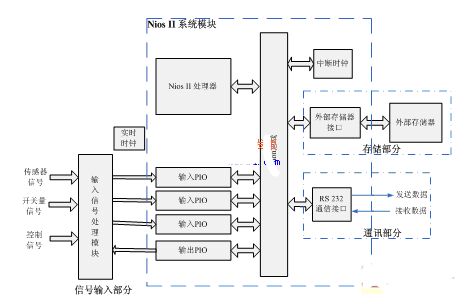
　　该系统的软件算法流程如图4所示，FPGA通过超声波传感器采集距离信息，并进行距离信息的存储以完成被检测物体的运动状态判断，当物体处于静止状态时则使用一维卡尔曼滤波算法对含噪声的距离测量值进行滤波去噪;当物体处于运动状态时，则使用二维卡尔曼滤波算法对含噪声的距离测量值进行去噪和优化处理，并可以利用关系矩阵和滤波算法得到运动物体的速度值。