探究分贝每倍频的意义和关系

　　在做滤波器、放大器或者EQ电路设计时，通常需要关注频率与强度的关系，这就是波特图。滤波器、放大器的波特图通常有两部分组成：幅频特性图和相频特性图，这两种图从不同的角度描述滤波电路的特性。在我接触到的EQ电路中，只关注幅频特性关系。幅频特性图中横坐标为频率，单位为Hz，纵坐标为对数关系，通常用分贝(dB)表示，计算关系为20log(Au)。一个典型的波特图如下图所示：

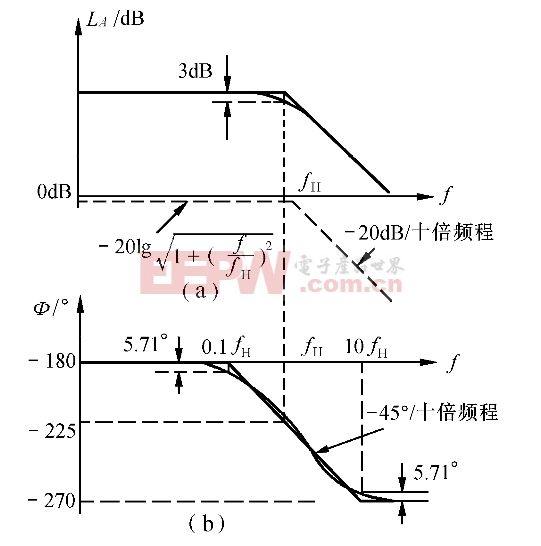
　　在一些书籍的描述中，经常会出现dB/2倍频、dB/6倍频和dB/10倍频，这都是为了更好的描述幅频特性关系而引入的描述。现在我们先以dB/2倍频为例进行详细说明。

　　首先从数学的角度来分析该单位的意义：纵坐标dB每增加1的dB横坐标频率将要增加2倍，严格意义上来说是以2倍频率的速度来进行纵坐标强度的判断，这样一来，比用1倍频率的横坐标变化量有更快的描述。从电子学方面看，采用2倍频作为标准时，虽然在-3dB位置的频率确认有了一定的模糊，但是，可以从幅频特性图中更加准确的得出在2倍频处的幅度特性。同样，dB/6倍频和dB/10倍频也是这个道理。

　　进一步，在滤波器和运放电路设计中，经常用到-3dB/倍频、-6dB/2倍频和-20dB/10倍频来描述电路特性，现在解释下为什么采用这样的描述。

　　-3dB/倍频:20log(Au)=-3 Au=0.707 也就是说频率增加1倍，幅度降低到原来的0.707

　　-6dB/2倍频:20log(Au)=-6 Au=1/2 也就是说频率增加2倍，幅度降低到原来的1/2

　　其他数值的分贝倍频关系可以同过以上公式进行计算，一般这么做都是为了方便频率得出放大倍数与频率的关系。

　　这些描述在数学角度来说有出力不讨好的苗头，但是，在电子学方面，却很形象的描述出了关键频率点和幅度之间的关系。

　　我们明白了不同倍频之间的意义之后，下一步在来分析计算下不同单位倍频之间的关系，现在我们以-3dB/倍频和-20dB/10倍频为例进行计算。这其实就是纯粹的数学变换，也顺便说明了一个道理，数学学科深入、渗入到了社会学科的不同领域。

　　在-3dB/倍频中，假如其波特图变化如下：

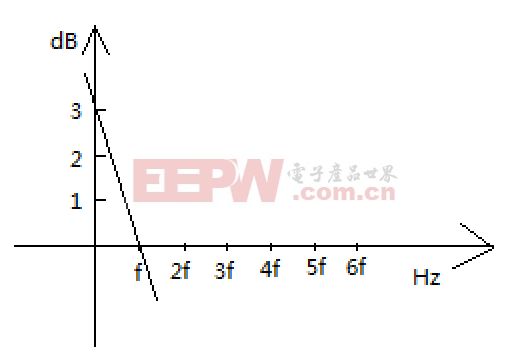
　　从数学角度来理解分析-3dB/倍频，依据上图来看，横坐标为倍频，纵坐标为强度dB，用数学的表达式为

　　y=-3x+1(该式子很好的描述了频率每增加一倍，强度减小3)

　　那么当横坐标为10倍频的时候，其波特图如下所示

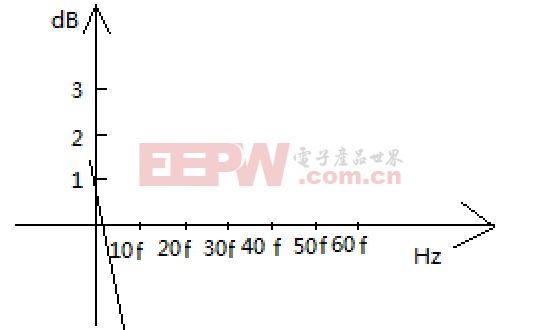
　　用数学表达式表示上图的数学关系为

　　y=-28x+1(该式子表示为横坐标以10倍频率增加，每增加一倍，强度减小28dB)

　　这样，从数学角度明确了不同倍频下强度的变换关系，使不同的强度变化(斜率)表现的更加明显。

　　还有另外一种形式，特别是在波特图奇零点分析时，因为幅频特性曲线每经过一个零点斜率就会减小一倍，每经过一个极点就会增大一倍，所以会在幅频特性曲线中见到-10dB/10倍频、-20dB/10倍频的斜率。

　　经过以上的数学分析，我们明白了不同分贝每倍频之间关系，这样，在以后碰到不同数值和不同分贝每倍频时，不能从数值上表示大小，只有变换为相同倍频的时候才能比较大小，这点必须要注意。