有源滤波器中的相位响应——低通和高通响应
本文旨在考察滤波器传递函数本身的相位偏移。虽然滤波器主要是针对幅度响应而设计的,但在延时仿真、级联滤波器级,特别是过程控制环路等应用中,相位响应可能非常重要。
本文引用地址:http://www.amcfsurvey.com/article/276095.htm本文将集中探讨低通和高通响应。我们先来回顾一下,有源滤波器的传递函数可以视为滤波器传递函数和放大器传递函数的级联响应(图1)。
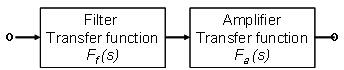
图1.作为两个传递函数级联的滤波器
首先,我们将重新考察一下传递等式的相位响应。
对于单极点低通情况,传递函数的相移为:
在等式中,表示弧度频率(=2πf弧度/秒;1 Hz=2π弧度/秒),表示滤波器上的弧度中心频率。中心频率也可称为截止频率。就相位而言,中心频率指相移处于其范围50%时的频率。由于弧度频率当作一个比率使用,因此,频率比(f/fo)可以方便地替代。
图2(左轴)在中心频率以下二十倍频程至中心频率以上二十倍频程的范围内对等式1进行了评估。由于单极点低通 的相移范围为90°(0°至90°),因此,中心频率的相移为–45°。当时,归一化中心频率为1。
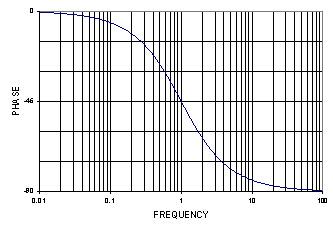
图2.单极点低通滤波器(左轴)和高通滤波器(右轴)在中心频率为1时的相位响应。
类似地,单极点高通滤波器的相位响应计算公式为:
图2(右轴)在中心频率以下二十倍频程至中心频率以上二十倍频程的范围内对等式2进行了评估。中心频率(= 1)的相移为+45°。
如果低通 通带定义为低于截止频率的频率,高通通带定义为高于中心频率的频率,注意,最低相移(0°至45°)处于通带中。相反,最高相移(45°至90°)出现在阻带中(高于低通截止频率和低于高通截止频率的频率)。
在低通情况下,滤波器的输出落后于输入(负相移);在高通情况下,输出先于输入(正相移)。图3展示的是下列波形:输入正弦波信号(中部轨迹)、1 kHz截止单极点高通滤波器输出(顶部轨迹)和1 kHz截止单极点低通滤波器输出(底部轨迹)。信号频率也为1 kHz——两个滤波器的截止频率。45°的波形超前和滞后情况显而易见。
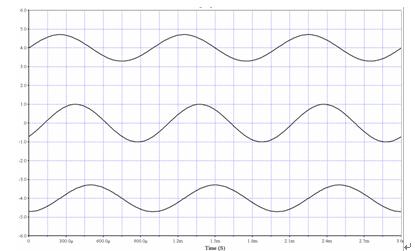
图3.单极点高通滤波器(顶部轨迹)和低通滤波器(底部轨迹)的输入(中部轨迹)和输出。
对于二阶低通情况,传输函数的相移近似值为:
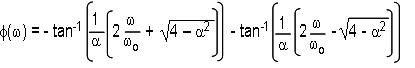
滤波器相关文章:滤波器原理
滤波器相关文章:滤波器原理
低通滤波器相关文章:低通滤波器原理
电源滤波器相关文章:电源滤波器原理
高通滤波器相关文章:高通滤波器原理 数字滤波器相关文章:数字滤波器原理






评论