指纹识别中的图像处理研究------指纹图像的特性分析 (二)
2.2纹理图像的特征及描述
本文引用地址:http://www.amcfsurvey.com/article/265776.htm纹理是以象素的邻域灰度空间分布为特征的,因此无法用点来定义,关于图像纹理的精确的定义迄今还没有一个统一的认识,本论文引用一个比较流行的定义如下。纹理是指图像强度局部变化的重复模式。纹理形成的机理是图像局部模式变化大小,一般无法在给定的分辨率下把不同的物体或区域分开。这样,在一个图像区域中重复出现满足给定灰度特性的一个连通象素集合构成了一个纹理区域。最简单的例子就是在白色背景下黑点的重复模式;例如,打印在白纸上的一行行的字符就构成了纹理;图2.3是一个纹理图像的例子。

目前,纹理分析包含有三个主要的问题,分别是:纹理分类、纹理分割和纹理图像恢复。由于本论文指纹图像的分割与纹理分割技术关系密切,故在此对纹理分析的方法进行简单的阐述。比较常用的方法有两种,一种是灰度共生矩阵测量方法,另一种是自相关函数法。
2.2.1灰度共生矩阵
灰度共生矩阵(co-occurrence matrix)P[i,j]是一个二维相关矩阵,其定义如下:首先规定一个位移矢量d =(dx,dy),然后,计算被d分开的且具有灰度级i和j的所有象素对个数。位移矢量为(1,1)是指象素向右和向下各移动一步。显然,灰度级数为n时,同现矩阵是一个n×n矩阵。例如,考虑一个具有灰度级0,1,2的简单5×5图像,
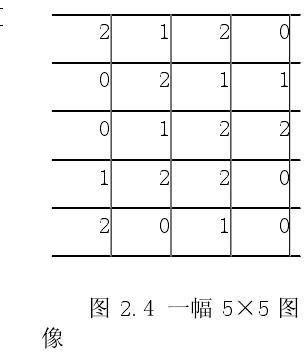
如图2.4所示,由于仅有三个灰度级,所以P[i,j]是一个3×3矩阵;在5×5图像中,共有16个(规定距离矢量d = (1,1)的情况下)象素对满足空间分离性;首先,计算所有象素对的数量,即计算所有象素值i与象素值j距离为d的象素对数量,然后把这个数填入矩阵P[i,j]的第i行和第j列,例如,有三对象素值为[2,1],因此在P[2,1]项中写3,所以象素对统计完后的矩阵如图2.5所示。
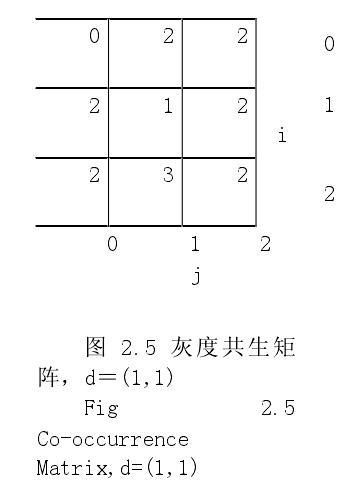
由于具有灰度级[i,j]的象素对数量不需要等于灰度级[i,j]的象素对数量,因此P[i,j]是一个非对称的矩阵,P[i,j]与象素对的总数之比称为规范化矩阵;在上面的例子中,每一项除以16就得到规范化矩阵,由于规范化矩阵P[i,j]的各元素值总和为1,因此,可以把它视为概率质量函数。
灰度共生矩阵表示了图像灰度空间分布,这可以很容易用下面的一个简单例子来说明。考虑一幅棋格为8×8的二值化图像,如图2.6所示,其中每一个方格对应一个象素。
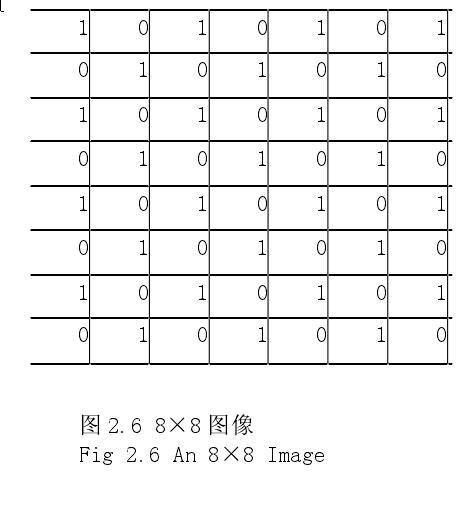
由于两级灰度,所以P[i,j]是一个2×2的矩阵。如果仍然定义距离矢量d =(1,1)则得到归一化矩阵P[i,j],如图2.7所示。由于象素对的结构的规则性,象素对仅仅出现[1,1]和[ 0,0].矩阵的非对角元素为零。

从上面的例子可以看出,如果黑色象素随地分布在整幅图像上,没有一个固定的模式,则灰度共生矩阵中不具有任何灰度级对的优先集合,则此时的矩阵元素值是均匀分布的,用于测量灰度级分布随机性的一种特征参数叫做熵(entropy),定义为

当矩阵P[i,j]的所有项都为零时,其熵值最高,这样的矩阵对应的图像不存在任何规定位移矢量的优势灰度级对。
2.2.2自相关函数法
一幅N×N图像的自相关(Auto-correlation)函数p[ k,l]定义为式(2.13)
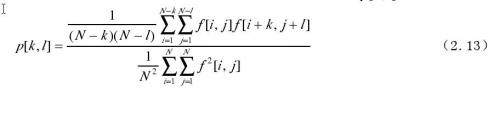









评论