3-D轮廓测量中相位解包裹应用
在对微/纳机电系统(micro/nano electro me-chanical system,MEMS/NEMS)结构的特性参数进行测量和MEMS/NEMS可靠性进行测试的过程中,常要求对结构表面的三维轮廓、粗糙度、微小的位移和变形等物理量做精密测量[1-3]。目前显微干涉法凭借其高精度、高垂直分辨率、测量简单快捷、无损等优点,成为这类测量中最常用的手段之一[3-5]。
在使用相移显微干涉法对MEMS/NEMS结构表面进行测量时,先通过驱动电路驱动参考镜产生次波长量级的光程变化,即可由电荷耦合器件摄像机(CCD)和图像采集卡获得一组时间序列上的相关干涉图像,然后由干涉图的光强信息解算出被测表面的相位值,提取包裹的相位信息,最后通过一定的相位解包裹算法得到被测表面真实的相位信息和相应的表面高度,从而得到被测结构表面的3-D轮廓[5-6]。由此可见,相位解包裹,也就是相位展开是微结构表面3-D轮廓测量中至关重要的一步.用于相位展开的方法很多,但通常都具有很强的针对性和局限性.而微纳结构的表面轮廓复杂,并且经常含有孔洞、沟槽、突起等特征形状,传统的解包裹算法不能绕过这些非理想数据区域,并且导致的误差会在被测面内传播,以致影响整个相位展开的结果。这里提出一种基于模板的广度优先搜索的相位解包裹方法,它通过模板的使用来剔除对相位展开有影响的非理想数据区域,使解包裹算法能够绕过这些区域进行,从而得到比较可靠的结果。
1 基于模板的相位解包裹
1.1 相位解包裹
通过相位提取算法,包含在光强中的代表被测物表面高度信息的相位值被提取出来。但在实际测量中,由于物体表面高度的相位变化通常都远远超出一个波长周期。因此,各种相位提取算法计算出来的相位值均是以反正切函数的形式表示,即得到的相位分布被截断成为多个2π范围内变化的区域,形成包裹相位。为最终得到被测表面真实的高度信息,必须将多个截断相位的区域拼接展开成连续相位,这个过程称为相位解包裹,或相位展开[6]。干涉测量中要求相邻两像素点的相位差小于2π,否则无法恢复其真实相位。当满足这个要求时,真实相位的差值则与包裹相位间差值再进行包裹运算W2的结果相等,即:
Δφ(n) = W2{ΔW1[φ(n)]} (n =1,2,…,N) (1)
式中Δ为差值运算,φ(n)是第n个像素点对应其包裹相位W1[φ(n)]的真实相位,N为像素点数。因此,通过对包裹的反正切函数主值差进行求和运算即可实现相位展开[7]:
φ(m) =φ(0)+∑mn=1W2{ΔW1[φ(n)]}(2)
MEMS/NEMS表面3-D轮廓测量针对的通常都是连续变化的结构表面,符合相邻像素点相位差小于2π的要求,因此依据式(2)所示的原理即可逐点实现相位展开。
1.2 基于模板的相位解包裹
随着相位展开技术的深入发展,相位解包裹算法层出不穷[7-8]。如果仅仅应用于简单区域(未展开相位图中不存在非理想数据点)的相位展开,使用普通的基于深度的优先搜索算法即可达到目的。它通过使用阈值来判断2π相位跳变,然后建立补偿函数,最后将未展开相图与补偿函数相加,得到展开后的相位图。此算法非常简单快捷,图1是应用于一个简单区域的相位展开结果,左边为被测表面的包裹相位图,右边为其相位解包裹后的表面轮廓图。

图1 使用传统相位解包裹算法对简单区域进行相位展开的结果
然而,MEMS/NEMS结构经常具有比较复杂的轮廓,含有孔洞、沟槽、突起等特征形状,被测表面也可能存在缺陷,例如表面镀膜脱落或者粘附上灰尘等,再加上阴影和噪声等的影响,用普通的相位展开方法就可能引入误差,并且误差会传播到在当前像素点之后展开的所有点。图2为使用传统相位解包裹算法对含有非理想数据点的圆形薄膜进行相位展开的结果,左边为薄膜表面的包裹相位图,右边为其相位解包裹后的表面轮廓图。

图2 使用传统相位解包裹算法对含有非理想数据区域进行相位展开的结果
为了能在相位展开过程中绕过非相容点(包裹相位图中的非数据点和进行相位展开运算时可能产生误差的非理想数据点的总称),引入基于模板的广度优先搜索算法,它是一种逐点展开的生长算法.在相位展开运算之前,先用模板将非相容点标记出来。相位展开过程是从任意的一个相容点开始,然后均匀地向其邻域弥散生长,得出其邻域的展开相位值,再一周一周扩大,直至整幅图像。在其遍历过程中,遇到由模板标记的非相容点时,就暂时绕过而不做处理。用此方法处理的像素点都是相容点,即好的数据点,因而能够大幅度地提高相位展开的质量。
2 标记模板的方法及实验结果
用以标记非相容点的模板可以通过多种途径获得。根据不同应用的需要,可以选择实现不同功能的不同复杂程度和不同灵敏程度的模板标记方法.本文提出三种不同类型的模板标记方法,用以在不同的应用需求下选择使用:1、子区域相容性判断法;2、边缘检测法;3、干涉图灰度差值提取法.对应于不同标记模板的方法,我们给出了它们应用于相位解包裹算法中的具体应用实例,各方法均由MATLAB编程实现。
2.1 子区域相容性判断法
2.1.1 方法
这种方法在包裹相位图的基础上进行判断。判断一个像素点是否相容,需要利用其周围的另外三个像素点的信息。这四个像素点组成一个2×2的子区域(图3)。按顺时针方向计算这四个像素点两两之间的灰度值之差,得到Δ1、Δ2、Δ3、Δ4;然后确定一个阈值T(如T=π),该阈值就是用来判断相位条纹跳变边界的那个“固定阈值”,并由此阈值判断Δk,(k=1,2,3,4):如果|Δk|>T,即可认为路径穿过了跳变的界线,此时,若Δk>0,则Δk=Δk-2π,若Δk0,则Δk=Δk+2π,目的是将Δk限定在-π到π之间;最后求ΣΔk,再次作判断:如果ΣΔk=0,则该点定义为相容点,如果ΣΔk≠0,则该点定义为非相容点[6]。

图3 标记2×2区域相容性示意图
2.1.2 实验结果
图4是一幅通过模拟得到的包裹相位图(左)及使用子区域相容性判断法得到的模板图(右)。包裹相位图中的黑色小方块是加入的非相容区域,从模板图可以看出,使用子区域相容性判断法可以将此非相容区域很好地提取出来,然而,它在识别出噪声点的同时,一部分相位跳变边缘也被识别成了非相容点,以至于相位解包裹之后一些原本好的数据点也被绕过,见图5。

图4 模拟的包裹相位图(左)及使用子区域相容性判断法得到的模板图(右)

图5 使用子区域相容性判断法获取模板得到的相位展开结果
子区域相容性判断法理论上可行,但实验结果证明其不太适合用于实际应用,特别是噪声多,结构复杂的测试.但由于此方法运算速度非常快,而且对噪声、断点等灵敏度很高,所以当图像区域小,噪声点远离相位跳变边缘时,仍可以考虑使用。
2.2 边缘检测法
2.2.1 方法
此方法在由干涉图合成的亮场图像上运用边缘检测算法来提取非相容区域的边缘.在五步相移干涉测量中,由得到的五幅干涉图像可以合成为被测表面的亮场图像[9],公式为: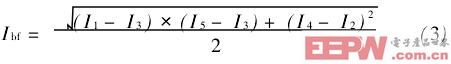










评论