飞行体姿态角的测试方法

　　飞行体姿态角的测试方法有很多种，如磁敏传感器、高速摄影仪、加速度计法以及陀螺仪等。各种方法都有其优点及应用局限，适用于不同的应用场合。某小型飞行体飞行过程中所受过载较小，姿态角变化不大，可容纳测试仪的空间有限，针对该小型飞行器姿态角测试，提出了一种基于陀螺仪的姿态角存储测试方法，介绍了具体实现方案。

　　2 姿态角测试系统设计

　　磁敏传感器法通常只是作为一种辅助测试手段，高速摄影法易受天气影响也限制了它的应用。加速度计法有着低成本、低功耗、高可靠性等优点，但是理论计算及安装复杂限制了该方法的应用，在国内多以理论研究为主。而陀螺仪法在过载不太大的场合应用方便，成为此飞行器姿态角测试的一个很好的选择。飞行体的姿态运动是飞行体绕自身质心的转动运动。在引入刚体假设和坐标系转换的概念后，飞行体的姿态定义为飞行体坐标系相对于参考坐标系的旋转变换。

　　2．1 陀螺仪姿态角测试原理

　　在对刚体的转动运动进行解析描述时．常应用欧拉角或卡尔丹角。卡尔丹角适用于姿态角变化较小的场合，因此．用卡尔丹角进行描述。取初始时刻飞行体坐标系Oξηζ为固定坐标系，0xyz为与飞行体固结的动坐标系。卡尔丹角选取的方法是，首先绕ξ轴转过α角，到达0x1y1zl的位置；再绕y1轴转动β角，到达0x2y2z2的位置；再绕z2轴转动γ角，到达0xyz的位置。转动关系如图l所示。

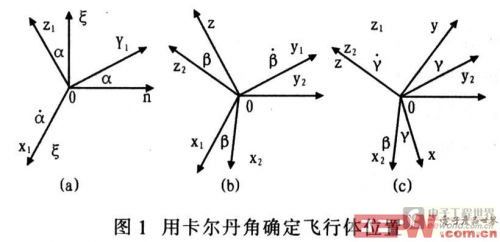
　 α、β以及γ分别为沿0ξ轴、0y1轴与0z轴的角速度分量，三次转动如式（1）所示：

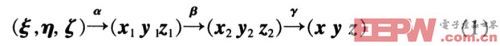
　　在此，以cx表示cosx、sx表示sinx，正切以tgx表示。各次转动相应的方向余弦矩阵分别为

　　飞行体的角速度ω，可以表示为：

　　式(7)为卡尔丹角表示的运动学微分方程，其中ωx、ωy及ωz分别为陀螺x轴、y轴及z轴的输出。积分此式，可得卡尔丹角。

　　2．2 系统实现

　　研究存储测试技术之后，设计了存储测试系统。体积微小和测量时不需要引线即不需要对外界的电磁辐射是他的最突出特点。在动态参数的存储测试领域，测试仪要随被测体一起运动，要求测试系统具有体积小、功耗低及抗高过载等特点，下面将结合系统设计阐述这些要求的相应解决措施。

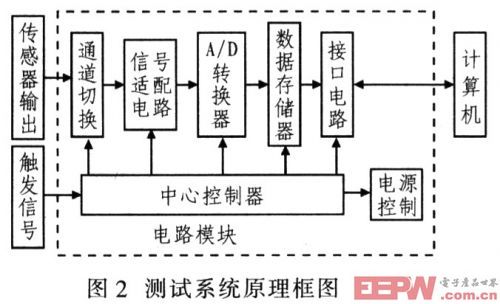
　　主控器件能否正常工作，是整个系统能否可靠获得被测参数的关键。CPLD输入和输出引脚的原始电平可预先设定，开机即能达到预定电平，状态明确。信号传输效率高，适合高速采样场合。可编程逻辑宏单元或逻辑块之间的相互连线在同一封装内，受外界干扰影响小，电磁兼容(EMC)性能好。综上所述，CPLD具有逻辑性强、响应时间快、程序不易跑飞等特点。为此选用CPLD作为主控器件，设计尽量简单可靠的器件内部逻辑，以确保整个测试过程系统的正常工作。本系统存储容量为512 Kxl2 bit，负延迟为128 Kxl2 bit，采样频率为8 kHz。测试系统原理框图如图2所示。