任意噪声和约束下的最佳数字滤波器设计

　　摘 要：为提高数字谱仪的能量分辨率，利用约束最优化方法提出了一个在任意平稳噪声背景下直接设计最佳数字有限冲击响应(FIR)滤波器的方法。该方法易于附加任意时域和频域约束(平顶、基线恢复等)。详细给出了最佳滤波器的设计推导过程，并在设计实例基础上，分析了滤波器的时域、频域响应和不同约束条件下的最大信噪比曲线。结果证明，该方法能够有效去除基线漂移和弹道亏损，得到了约束条件下的最大信噪比，适合在未知系统噪声特性情况下的高计数率、高精度谱仪中使用。

　　关键调：最佳滤波器；数字谱仪；基线恢复

　　在数字谱仪中，探测器输出信号直接进行模数转换，经过数字滤波可以改善模数转换器(ADC)的线性和精度，因此数字滤波器的设计成为提高整个系统性能指标的关键。谱仪滤波器的设计，除尽可能提高信噪比外，通常还要考虑成形脉冲形状的要求，例如窄成形脉冲以减少堆积，渡形顶部平坦以减少弹道亏损等。

　　文提出了一种可以附加任意约束、在任意噪声背景下设计最佳模拟滤波器的方法，由于设计出来的是权函数，无法直接用于数字滤波，而且通过抽样最佳模拟滤波器得到的数字滤波器不是最优滤波器。文提出了移动窗口解卷积的设计方法，此方法无法考虑噪声影响，仅适合指数衰减形式的脉冲。文提出了惩罚最小方差方法设计最佳滤波器，其约束必须写成二次型的形式，添加约束比较困难，并且在多个约束的条件下，无法综合出严格的平顶。

　　有限冲击响应(FIR)滤波器没有反馈通路，某个时刻的输出直接由此时刻之前固定时间长度的输入决定，其结构特点易于通用数字信号处理器(DSP)芯片或在线可编程逻辑阵列(FPGA)实现。本文提出了一种基于信噪比准则的直接设计最佳数字FIR滤波器的方法。

　　l 问题的提出

　　假定噪声是和输入信号不相关的平稳随机过程，在已知输入信号形状噪声自相关函数的条件下，寻找满足约束条件的FIR滤波器，使输出信号的信噪比最大。先求得以滤波器系数为变量的信噪比表达式，然后添加适当约束，把求解最佳滤波器的任务转化成求解一个约束最优化问题。

　　1．1 SNR的计算

　　设噪声的自相关函数为{r(i)}，待求的N阶FIR滤波器的冲击响应为h={h(0)，h(1)，…，h(N一1)}T，采样得到的信号为{s(i)}，由已知波形的输入脉冲信号{x(i)}和噪声信号{n(i)}相加而成。从{x(i)}选取N个连续数据，使N个数的平方和最大，重新排列标号，使得选取的数据为{x(1)，…，x(N)}。

　　1．2 时域约束的添加

　　滤波后的脉冲为输入和FIR滤波器的卷积，即成形后脉冲各点是输入以h为系数的线性组合，这样把在时域的约束转化成了对h的约束。以添加平顶约束为例，设要求输出脉冲的平顶宽度为m，即要求y(N)直到y(N一m)相等，则有：

　　1．3 频域约束的添加

　　FIR的频率响应为

　　式中DTFT表示离散Fourier变换。

　　频率响应函数为FIR滤波器系数的线性组合，因此把在频域的约束也转化成对h的约束。为了去除基线漂移，FIR的频率响应在0 Hz处为0，即

　　平顶和去除基线这两个约束构成了一个线性方程组。这些约束相互之间是独立的，否则可以从这些方程中选取出最大无关向量组来构成A。综合式(1)和(2)，构成一个线性约束最优化问题。

　　2 问题的求解

　　在有约束情况下，约束线性方程组把N维线性空间直和分解分成两个空间：滤波器允许空间(任意向量都满足约束条件)及此空间的正交补。把无约束下的解向滤波器允许空间投影就得到了约束条件下的最佳解。

　　2．1 无约束的情况

　　噪声的相关矩阵为实对称正定矩阵，可以共轭对角化为

　　2．2 有约束的情况

　　在有约束的情况下，h1受约束条件的限制，约束条件转化成一个线性方程组，即

　　假设共有m个独立约束，则约束方程组的解构成一个N一m维线性空间，称为滤波器允许空间，记做V，则V垂直于矩阵的行空间。把作QR分解得到

　　由于P为单位正交阵，P的前m列构成的行空间一个正交基底，后N一m列构成V的一个正交基底。把分解成V中的向量和与V垂直的向量，有

　　当约束方程中的b不为0时，则h1被限制在一个仿射空间内，把h1平移到此空间中的任意一点，就变化成和b为0一样的解法。在约束为非线性时，可以采用数值最优化方法求解。

　　2．3 求解结果的分析

　　无约束的情况：在白噪声情况下，自相关矩阵为噪声功率乘以单位阵，此时的解简化为h=kx。也就是说，滤波器与已知信号的形状成正比，对应于模拟情况下的匹配滤波器。在有色噪声情况下，相当于x先对输入噪声进行白化处理，得到白噪声，因此，有色噪声情况下的最佳滤波器是白化滤波器与其后的白噪声匹配滤波器的级联。

　　在有约束的情况下，给定的约束条件限制了滤波器的范围，最佳滤波器为无约束条件下的最佳滤波器向滤波器允许空间的投影。

　　2．4 输入波形和噪声自相关函数的计算

　　在已知前放和抗混叠滤波器参数的情况下，可以直接计算得到输入信号。由于RC参数的不精确，计算得到的波形和实际的波形有差别，可以通过估计极零点的方法加以修正。或者平均多次ADC的采样来减小噪声，从而得到输入信号的波形。

　　在已知噪声功率谱的情况下，可以通过Fourier反变换得到连续时间下的自相关函数。在很多情况下，可能不知道准确的系统噪声特性，可以通过采样无信号输入时ADC的输出来计算系统的自相关函数。如果采样得到的噪声序列是{x(i)}，那么怙计自相关函数为

　　3 设计结果

　　以下面的参数为例进行分析：输入脉冲有3个相等的实极点，时间常数为200 ns，幅度归一化为1，采样频率为50 MHz，噪声为白噪声。

　　3．1 滤波器长度的选取

　　滤波器的长度越长，系统能够得到的信噪比越大。但成形后的脉冲宽度也越宽，因而容易产生堆积。在设计实际的滤波器时，要根据计数率和噪声等因素综合考虑，选择合适的长度。一般在选取输入波形数据段时，如果段数据平方包含的面积和整个波形平方后的总面积相差不多，则设计出的最佳滤波器的信噪比就很接近理论上的最大值。在下面讨论中，把实际滤波器的信噪比以滤波器无限长时的最大信噪比进行了归一化。在上述输入条件下，FIR滤波器长度取70时的信噪比已达到0．998。

　　3．2 设计结果

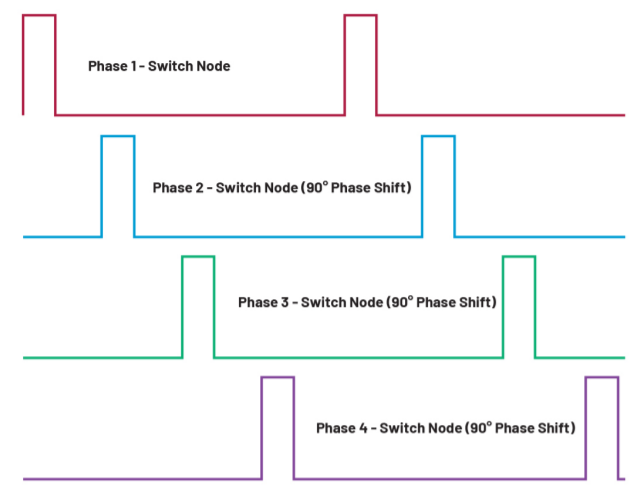
　　取滤波器的长度为70，在无约束、有平顶宽度为20、去除基线和既有平顶叉去除基线4种约束情况下分别求解，FIR滤波器的设计结果如图l所示。有平顶约束的FIR滤