基于FPGA的定时同步算法设计

摘要 文中对适用于高速突发通信的基于数字滤波平方的定时同步算法进行了研究。通过对在高速数据传输通信中，该定时同步环路的定时误差估计模块进行并行结构实现，大幅降低了系统对于时钟的要求，且更加易于实现;将文中所提定时控制部分与其他文献中的方法做了对比，表明所用方法可以达到更好的效果。最后进行的Matlab仿真以及硬件实现，结果表明，该环路可以实现突发与非突发情况下的高速数传定时同步。

目前，数字通信系统正向高速全数字化方向发展。在全数字接收机定时同步中，主要包括两个关键点：定时误差估计和定时控制。传统的定时同步方法中一般直接调节本地采样时钟以达到采样最佳的效果，而在全数字接收机中，本地采样时钟不变，通过计算定时误差控制产生重采样时钟达到最佳采样。通过产生重采样时钟达到定时同步的方法常用的有Gardner算法和数字滤波平方法。二者同属定时同步中的内插法，对载波信号不敏感，可以先于载波同步进行，差别在于Gardner属于反馈式，而数字滤波平方法属于前馈式，所以后者的同步时间更短更适合处理突发信号，因此在存在突发情况的全数字接收机中得到了广泛应用。数字滤波平方法适用于正在研究项目中，要求可以处理突发情况下MPSK与MQAM调制信号的定时同步，并且在高速通信情况下，通过对算法的定时误差估计模块进行并行结构实现，可以大幅降低对于时钟的要求，所以对数字滤波平方法的研究是必要和有意义的。

1 定时同步原理

对于一般的线性调制信号，有

其中，cn为发送的符号数据;g(t)：gT(t)×gR(t)为系统脉冲响应;gT(t)为发送端成型滤波器的脉冲响应;gR(t)为接收端匹配滤波器的脉冲响应;T为符号周期;s(t)为慢变的采样时间误差;B(t)为载波相差，这里不考虑载波相差，即B(t)=0，n(t)为高斯噪声，n(t)～N(0，2δ2)，其同相分量和正交分量的方差均为δ2。

对接收信号r(t)以采样率N/T采样可得

rk=r(kT/N) (2)

然后对采样后的信号取模并平方，得xk样本信号，该样本信号中包含有一个频率为1/T的频谱分量，该频谱分量中就包含有定时误差信息。通过计算每一段长为LN(即LN个采样数据;L代表一次运算的符号数;N表示每个符号的采样点数;一般取N=4)的数据序列的傅里叶系数提取出来，该系数为

式中求出的定时误差

为ε的无偏估计。

2 定时误差估计

2.1 实现框图

根据式(3)，当N=4时通过公式变换可得定时误差估计实现框图如图1所示。

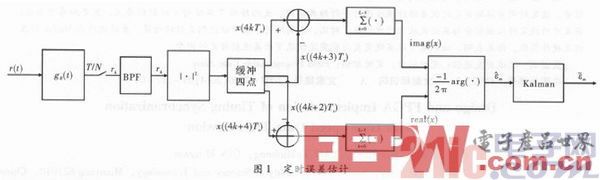
其中，匹配滤波之后，加入一个中心频率为1/2T，带宽为α/T的带通滤波器，用来滤除带外噪声，并在误差求出之后加入一个卡尔曼滤波器，用以对结果进行平滑。

2.2 误差估计的并行结构

针对高速数据传输时的通信，在定时同步的前端，ADC采样采取并行结构，也即ADC通过并行时间交织的采样方式进行4倍采样。然后匹配滤波器设计为并行转置型FIR，进行并行输出，输出的结果再次使用并行结构，分别求出式(5)中image(x)和real(x)，并行结构如图2所示。

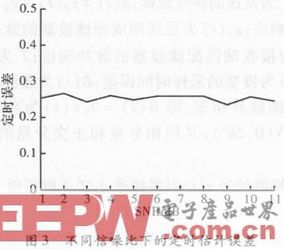
预设定时误差为1/4，在不同输入信噪比情况下验证定时误差估计的准确性，如图3所示。定时误差并行算法结构能够正确地估计定时误差。

3 定时控制

定时控制部分，文献提到用与Gardner算法中相同的控制方法，即环路滤波和NCO控制。在此，文中使用另外一种定时控制方法，获得了更好的效果。定时控制部分，文中采用定时估计算法，估计出的误差值去控制产生内插所要用到的整数间隔mk和分数间隔μk。

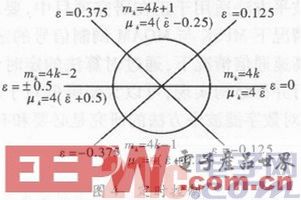
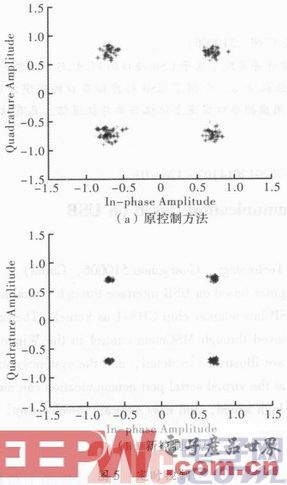
Gardner定时控制方法和新控制方法分别为两种定时控制方法在码速率为300 MHz，采样率为1.2 GHz，时偏为0.25T，SNR为15 dB时的星座图。从星座图可明显看出，新控制方法效果更好，星座图更加收敛。

4 Matlab仿真

仿真中，采用QPSK调制，匹配滤波器滚降系数设为0.35，符号率为300 MHz，采样率1.2 GHz，每个码元采4个点，信噪比设为15 dB，信道为高斯白噪声信道。

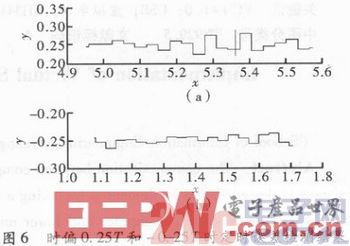
当时偏设为0.25T和-0.25T时，环路定时误差检测结果分别如图6(a)和图6(b)所示。通过图8可以看出误差检测结果是可信的。