反馈线性化直接方法的理论分析与改进
基于动平衡状态理论的反馈线性化直接方法的基本思想是:首先根据对被控对象的性能要求,设计出具有希望动态特性的线性参考模型;然后将参考模型的状态作为控制系统的动平衡状态,再利用李亚普诺夫第二方法设计控制律使系统对动平衡状态渐近稳定。这样被控系统的动态过程将收敛于参考模型给出的希望动态过程,从而使系统获得预期的性能。
这种方法分为两步:(1)按照希望的动态特性设计一满足要求的参考系统,这里常用线性系统因为它较容易分析和设计。(2)以模型参考系统的状态作为实际被控系统的被控动平衡状态,利用Lyapunov函数直接方法设计控制律使系统对动平衡状态渐进稳定。这里我们设计线性的参考系统Q指数稳定于原点,则这种方法的稳定问题在二维坐标系下的表示如图1所示。
1基于动平衡状态理论的反馈线性化直接方法的讨论

若让式(3)、(4)和式(5)直接成立,则只能达到局部渐进稳定。因此,我们仍应用backstepping设计方法中的虚拟控制的概念来设计。

但是,此方法也只能在局部实现,这是因为:使用改进的方法是使M→0,而非M=0,所以有两种情况,即M→O_和M→0+,而对于M→0+,就有可能使V(e)=-eTQe+2M大于零,此时仍需进一步讨论。
因此现在的问题有如下几个:
(1)使用改进的方法如何判别M的符号问题。
(2)u-a21x1-a22x2-a23x3=0与最后结果是否能相容值得验证。
(3)求得的控制率结果中分母项有可能为零,因此可能会引起震荡,此需要讨论和验证。
对于问题(1),我们可以这样来实现:因为总体的设计是使得V(e)=-eTQe+2M0,并且根据前面的假设当t→∞时,有V(e)→0,增强的条件是前述的M≤0,减弱的条件是-eTQe+2M0,即2M-eTQe,因此,我们的设计可以这样来进行:让M→0的速度快于eTQe→0,如此选择就能使原系统达到渐进稳定。对于问题(2)和(3),我们将进行讨论。
2改进的基于动平衡状态理论的反馈线性化直接方法
考虑如下的非线性系统:

由于Ad的所有特征值均具有负实部,因此可以找到正定矩阵P,使Q为一正定矩阵。若能选取控制向量ξ(x,xd,v,t),使M≤0,则V(e)0。若能选择ξ使M在所考虑的系统参数变化范围内非正,则可保证系统具有参数不确定时反馈线性化的鲁棒性。下面分情况考虑。


明显上述式(20)~(23)中任何一个等号均不能成立,再次引入一个Lyapunov函数来进行设计。此时我们仅以一种表达为例来介绍下面的设计过程。
现选择第二种表达,即:当[f(x,ξ,t)-Adx-Bdv]=-γe时,其中γ为一任意正数。

如果x3=x2d,则输入是不可测的,即输入无穷大,这在控制系统中是要避免的。但是,我们要注意的是分子亦是趋近于零的项,如果分子分母同时趋近零,那么我们的担心将是不必要的,如果分子趋近于零的速度比分母快,那么就更不用担心了。因此现在的问题转化为分析A和B是否存在的问题。两者的分子分母的解析式表达没有非常明确的联系,因为对于此在数学上暂时还没有找到解决的办法。但是可以在实验中观察到,即观察分子分母趋于零的速度,速度快且持续保持在零的为相对的低阶无穷小,在对某一类非线性系统设计时,如果分子是低阶无穷小,则此设计有效,如果是分母,则设计无效。
考虑如下的非线性系统:
使用改进的基于动平衡状态的反馈线性化方法使以上系统达到全局渐进稳定,设仿射非线性系统(34)中状态x1,x2的动平衡状态分别为x1,x2,它是下列线性系统的状态:

现在设x1(0)=0.3,x2(0)=1,x3(0)=-1,进行仿真时因为式中分母部分为零,得不到仿真结果并有出错提示为"division by zero"。因此去掉分式中分母部分进行仿真,其理由是因为设计的控制输入结果和3(xs-x3d)两项在t→∞时将为零,它们对于控制输入只是起一个调节作用,此时的仿真结果为如图2,3所示。
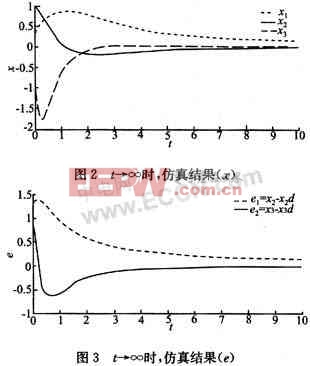
改变参数的值,设k1=0.1,k2=2,则仿真结果如图4、5所示。
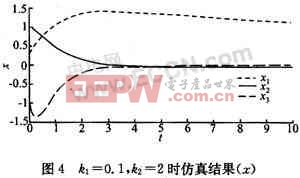
改变参数的值,设k1=2,k2=0.1,则无法得到满意的结果,Matlab有提示为"Warning:Fail-ure at t=3.258456e+000.Unable to meet inte-gration tolerances without reducing the step sizebelow the smallest value allowed(1.157636e_014)at time t."。其仿真后的图像如图6、7所示。
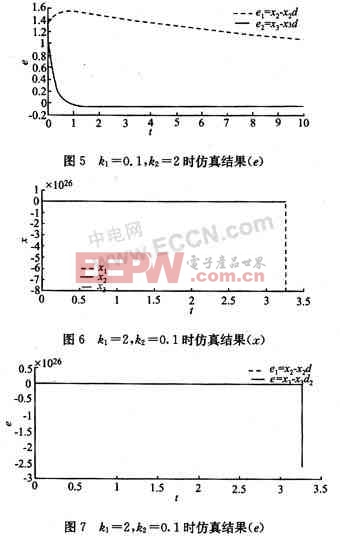
但是设k1=2,k2=3,并在分式中前面加一个系数5得仿真结果如图8、9所示。
设k1=3,k2=3,仍存在系数,则仿真结果如图10、11所示。
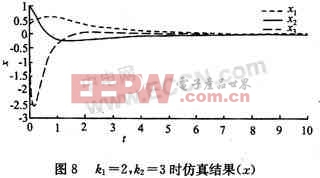

由以上各图我们得到以下结果:当k1=k2时,系统的状态收敛情况最好;当k1《k2时,系统的状态x1将不能稳定于零,而且误差e1=x2-x2d将存在并且比较大;当k1》k2时,仿真没有结果;在分式
前面加一个大于1的系数,仍去掉分母,其收敛效果将更好。
4结 论
本文对基于动平衡状态理论的反馈线性化直接方法进行了讨论、完善和补充,针对它在对仿射非线性系统进行设计时出现的问题,提出了改进的基于动平衡状态理论的反馈线性化直接方法,它在形式和方法上对基于动平衡状态理论的反馈线性化直接方法做了一定的改进,引用Backstepping设计方法虚拟控制的概念来对系统进行二次Lyapunov函数设计。



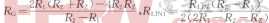

评论