可重组多功能大数运算器的小规模硬件实现
随着各种加解密算法密钥长度的逐步增加,在一些具有安全性需求的芯片设计中,大规格数据运算的硬件实现已成为硬件设计的主要考虑因素和设计难点.比如RSA等基于大数分解的公钥密码算法,虽然目前密钥长度已达1024位,但是仍然不能避免将被破解的厄运,致使密钥还需进一步增加.这种运算规格的增长不仅使加解密运算速度降低,而且增加了硬件实现的难度.
目前国内外对大数值运算器的研究,主要集中在大数模幂乘运算的实现上,其数学表达式为S=ABmodN.大数模幂乘一般用模平方和模乘来实现;对于一个指数B,模平方的次数是固定的,而模乘的次数是可以优化的.因此可在以下两方面考虑运算加速:(1)减少模乘次数;(2)提高大数模乘速度.针对第一种方案提出的加速算法有m进制方法、加法链法、Yacobi法;针对第二种方案有估商型系列算法和Montgomery系列算法_.以上各种方案或者需要预计算,占用较大的存储空间,或者需要设置专门的乘法单元,都是在牺牲规模的前提下提高运算速度.在对规模要求严格的安全芯片中,以上方法不再适用.而且,它们也并未涉及其他运算(如加、减、乘、除等四则运算)的大规格实现方法.
根据保密终端安全芯片CSTU(China secureterminal unit,国家密码委员会审批项目,产品型号SSX11)对运算速度要求不高(主频20 MHz)、对规模要求严格的设计需求,提出了一种小规模的大数值运算器设计方法.基于加法操作,在扫描链的配合下,全部用逻辑电路实现了包括加减乘除及模乘、模幂乘等多种运算功能,各功能支持的运算规格从8位一直扩展到2048位.经综合验证,在20MHz的主频下,设计规模只有13887门,完全适用于CSTU安全体系的面积优先的设计要求.
1 CSTU 安全芯片体系结构简介
随着人们对安全需求的不断增加,采用固定或单一加解密算法的产品已经无法满足人们的需求,目前的安全产品需要经常更换加解密算法甚至改变整个安全策略.适应这种需求常用的方法是在基本运算器之上,使用软件编程的方式灵活的实现算法的转换.但是面对不断升级的软件破解技术的挑战,以及软件方式的低速率性,各种加解密算法也由软件实现向硬件电路实现过渡.为解决这一矛盾.可支持多种加解密算法的硬件安全产品就应运而生,其中基于可重组方式设计的安全芯片无疑又具有领先优势.
CSTU保密终端安全芯片采用了可重组设计思想,综合分析了当前大量使用的DES,AES,IDEA,RSA,MD5等十余种加解密算法的实现过程,支持对称、公钥、摘要密码算法及用户隐秘算法,提供这些算法实现所需的IP平台,不同的用户可以根据自己的需要在平台上进行二次开发,形成自己定义的安全算法及策略.
CSTU安全芯片可用于保密电话、安全卡证或移动安全终端等产品中,这些产品的共同特点是对规模要求比较严格,对公钥密码算法的速度要求不高.为提供对公钥密码算法和数字签名算法的支持,大数运算器成为CSTU安全体系中关键的核心IP.根据实际需求,本设计在满足硬件规模尽可能小同时支持尽可能多的运算功能和多种规格的数据运算的条件下,最终保证整个系统的灵活性.
2 算法分析
2.1 模幂乘算法分析
模幂乘运算采用平方乘算法,将模幂乘运算转化为模乘和模平方运算实现.
平方-乘算法:一般地,求S=ABmodN,其中AN,BN;将指数B表示为二进制,即

观察算法,由于指数B化为二进制后的长度不确定,多数情况下高位会存在很多个0.如果完全按照该算法实现,指数B从最高位起开始运算,在第一个1出现以前,虽进行了多次运算,但D的值一直为1;当B出现第一个1后才进入有效的模乘运算.在具体实现时,设计专门的电路从高到低扫描指数B的每一位,当在找到第一个1之前,不做任何运算,找到第一个1时,使D=A,以后根据每次扫描的6[i]值,调用模乘实现运算.
经过对多种公钥加解密算法的分析——如RSA算法,通常公钥的有效位较短,而私钥有效位较长.加密中的模幂乘运算,指数有效位很少,所以上面的改进可大大减少模乘次数,加快加密过程.以目前常用的私钥和模数1 024 bit,公钥128bit情况为例,采用上述改进可减少896次不必要的模乘.解密过程使用中国余数定理(CRT),可有效降低解密指数的长度,整个算法的执行效率得到进一步提高.
2.2 模乘及模加的实现方法
模乘采用改进的Blakley加法型算法,原理与平方-乘算法类似,核心是将模乘转化为模加实现.如通常S=(A×B)modN,AN,BN可以按如下方式考虑.
将B表示成二进制:

由上式可知,可以像平方一乘算法一样,将模乘转化为模加实现.
一般模加运算表示为S=(A+B)modN,观察以上模乘及模幂乘算法原理描述,可知在其调用的模加运算中,因为AN且BN,则(A+B)2N,所以,
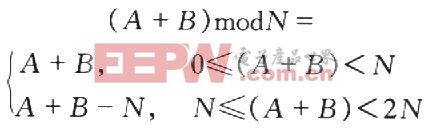
因此考虑在运算中同时计算(A+B)和(A+B-N)两个结果,运算完成后通过判断加法器与减法器的进位输出(CO)与借位输出(BO).决定哪个为本次模加的正确结果.同上,A,B,N均为l位的二进制数,若CO=1,则说明(A+B)为l+1位二进制数,必大于l位的N;若CO=0,则(A+B)和N同为l位,当BO=1时(A+B)N,当BO=0时N≤(A+B).
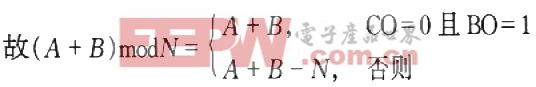
从而可以在一次运算中完成加法和求模过程,使模加的运算速度提高1倍.
2.3 其他功能实现
经过对多种公钥加解密算法及签名算法的分析,为提高芯片整体灵活性本设计还给出了对乘法、除法、求模、模加法逆、开方几种常用运算的支持.同样选择基于加减运算的算法实现,充分考虑算法对扫描链等已有逻辑资源的服用,设计出符合产品运算速度的面积最小化的系统.表1列出系统实现的其他功能模块采用的算法名称、详细算法及相关文献.

3 设计实现
以一个可以完成32位规格加、减、模加、增减量、移位等基本功能的ALU为基本运算单元,在扫描链逻辑的控制下,可以完成乘、除、开方、模乘、模幂乘等多种复杂运算.设计结构如图1所示.大数值运算器的外接口信号分以下三类.(1)控制:功能,规格以及源、目的指示;(2)数据:来自体RAM的源操作数,运算结果到RAM的反馈;(3)状态:运算结束,对体系相应状态寄存器的控制信号.
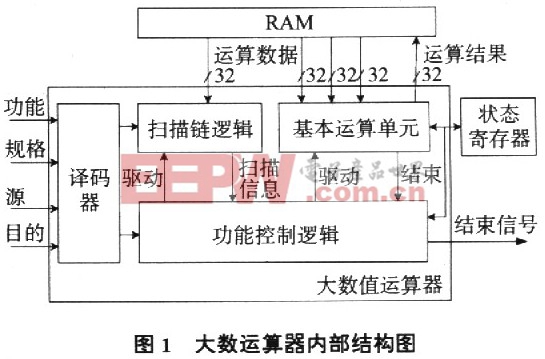
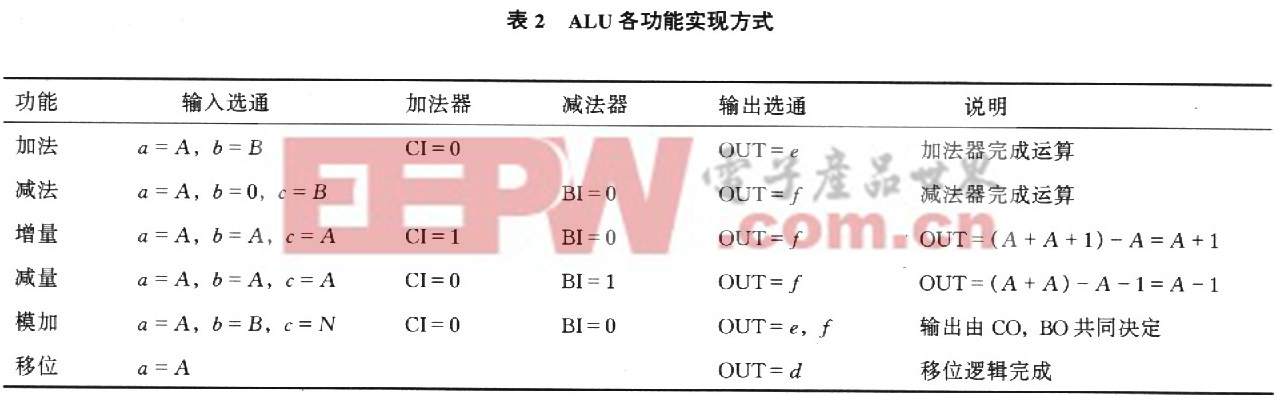
基本运算单元(ALU):可在单周期内完成32位加减、增(减)量、模加、左右移一位功能,其核心结构如图2所示,由输入选通控制MUX-IN,32位加法器ADD,32位减法器SUB,移位逻辑SF和输出选通控制MUX-OUT组成.

各功能在ALU中的具体实现方式见表2:
功能控制逻辑:完成各个功能的控制,可分为简单功能和复杂功能两类不同的控制.
1)简单功能:32位规格以上的加减、模加、增(减)量、移位功能.功能实现通过多周期迭代调用ALU相应功能实现,多次调用间保持进/借位传递.
2)复杂功能:模乘、模幂乘、乘除、开方功能.根据算法原理设计状态机,根据扫描链逻辑的配合信号,通过调用简单功能实现运算.
扫描链逻辑:当功能控制逻辑在完成复杂功能时,驱动扫描链逻辑动作.核心电路为32位的移位寄存器,扫描链逻辑可完成:待扫描数据的自动装载和切换;扫描数据高位0的自动去除,即自动找到第一个1,并给出标识信号;在使能信号的控制下从高到低自动扫描数据,给出扫描结果;扫描结束给出结束信号.
4 测试及结论
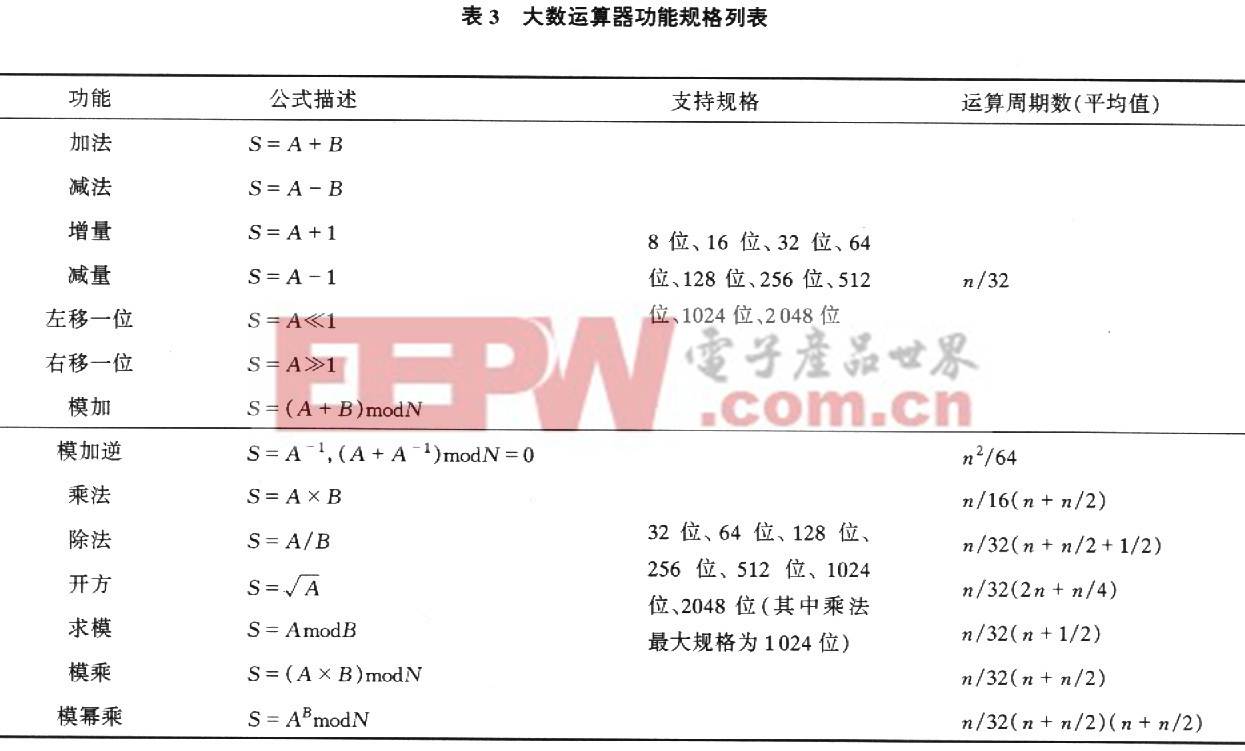
本文提出了一种用于可重组安全芯片的,面积优先、多功能、可重组的大数值运算器的实现方法设计支持的所有功能及规格如表3所示.所有模块均在ModelSim环境下通过了逻辑仿真,并在Xilinx公司的Virtex-Ⅱ系列FPGA产品XC2V6000上经过实际功能验证.
使用Synopsys公司Design Compiler综合工具,在台基电(TSMC)0.25μm工艺和安全芯片要求的20Hz时钟主频下的综合结果为13 887门.设计的结果与近年的几个大数值运算器的对比见表4.可见本设计虽然运算速度稍慢,但设计规模同比大大降低,完全符合CSTU保密终端安全芯片对面积优先的设计要求,速度也在设计允许范围内.






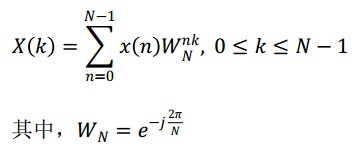

评论