冗余度TT-VGT机器人的神经网络自适应控制
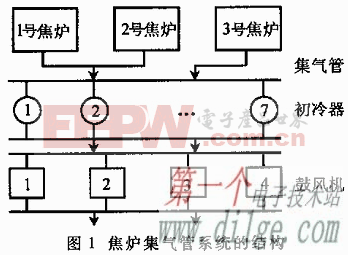
TT-VGT(Tetrahedron-Tetrahedron-Variable Geometry Truss)机器人是由多个四面体组成的变几何桁架机器人,图1所示为由N个四面体单元组成的冗余度TT-VGT机器人操作手,平面ABC为机器人的基础平台,基本单元中各杆之间由较铰连接,通过可伸缩构件li(i=1,2,…,n)的长度变化改变机构的构形。图2所示为其中的两个单元的TT-VGT机构,设平面ABC和平面BCD的夹角用中间变量qi(i=1,2,…,n)表示,qi与li(I=1,2,…,n)的关系如下[2]:
4 实例分析
以四得四面体为例,如图5所示建立基础坐标系,末端参考点H位于末端平台EFG的中点。设参考点H在基础坐标系中,从点(0.8640,-0.6265,0.5005)直线运动到点(1.8725,0.5078,0.7981),只实现空间的位置,不实现姿态。运动的整个时间T设定5秒,运动轨迹分为等时间间隔的100个区间。不失一般性要求,末端在轨迹的前40个区间匀加速度运动(a=0.2578),中间20个工间匀速度运动,最后40个区间匀减速度运动(a=-0.2578),开始和结束时的末端速度为。设各定长构件长度为1m,机构中各杆质量为1kg,并将质量向四面体各顶点对称简化。
传动装置的参数如下:
Ma=4.0×10e -3kg·m/V;Ba=0.01N·m/(rad·s -1);
近似认为各关节电动机轴上的总转动惯量在运动过程中保持不变,其值分别为:
J1=0.734kg·m2;J2=0.715kg·m2;
J3=0.537kg·m2;J4=0.338kg·m2
末端位置误差曲线如图6所示。从误差曲线可看出,用神经网络自适应控制的机器人位置控制精度较高,稳定性较好。
本文提出采用直接MRAC神经网络自适应器对机器人进行轨迹控制的方案;建立机器人状态模型,推导出自适应控制算法,并对冗余度TT-VGT机器人轨迹控制进行了仿真。结果表明,该方案控制误差较小,稳定性较好。




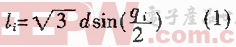








评论