FIR数字滤波器的MATLAB仿真和DSP的实现
本设计采用具有严格线性相位、稳定性好的FIR数字滤波器来实现滤波器的设计。MATLAB作为设计FIR滤波器的强有力工具,为设计应用提供了相应的工具箱,从而将复杂的程序设计简单化为函数调用,简化难度的同时还提高了效率。TMS320F2812DSP是TI公司推出的一款用于控制和数字信号处理领域的多功能、高性价比的芯片,其优良的性价比使其在数字信号的实时处理中得到了广泛的应用。本文介绍了采用MATLAB仿真技术和DSP来设计实现FIR数字滤波器。
1 数字滤波器原理
对于数字滤波器,描述系统特性用差分方程。设其输入序列为x(k),输出序列为y(k),则它们之间的关系可以用差分方程来表示:
y(k})+b1y(k-1)+…+bMy(k-M)=a0x(k)+a1x(k-1)+…+anx(k-N) (1)
其中,y(k)系数一般取1;b1,…bM及a0,…aN为常系数;
对于特定的系统,M和N为常数,分别代表输出最高阶数和输入最高阶数。

2 FIR数字滤波器设计方案
数字滤波器的设计有无限冲激响应滤波器(IIR)和有限冲激响应滤波器(FIR)两种选择。无限冲激响应滤波器的设计是借助模拟滤波器转换的设计方法,一般有公式和图表可查询,另外还有一些典型模拟滤波器可供选择,这种方法相对比较简单。有限冲激响应滤波器主要采用非递归结构,可以保证绝对的稳定,这有利于对谐波相位的分析。
在数字滤波器差分方程的基础上,如果全部ak=0(k=0,1,…,N),此时系统的输出只和输入x(n-k)有关系,则以上公式成为没有反馈的递归结构。设FIR滤波器的单位冲激响应h(r)为一个N点有限长序列,其中0≤r≤N-1。
则FIR数字滤波器的传递函数可以表示为
从FIR数字滤波器传递函数表达式可以看出,其传递函数是一个Z-1的N-1次多项式,它在z平面上有N-1个零点,没有极点(有时认为在原点上有N-1个重极点)。其传递函数实际上就是单位抽样序列的z变换。
当数字滤波器的技术指标确定后,可以用一定的方法去逼近,目前FIR滤波器设计主要有3种方法:窗函数法、频率抽样法和切比雪夫最佳一致逼近法。
FIR滤波器的设计任务是根据给定的技术指标确定一个传递函数H(z),使其频率响应满足给定的要求。这些方法设计出的滤波器特性都是在不同意义上对理想频率特性的逼近。3 FIR数字滤波器的设计

滤波器相关文章:滤波器原理
滤波器相关文章:滤波器原理
电源滤波器相关文章:电源滤波器原理
数字滤波器相关文章:数字滤波器原理




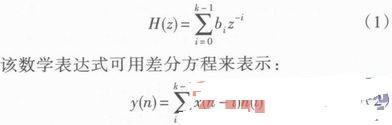


评论