基于小波理论的变压器励磁涌流和短路电流的判定

小波理论分析

小波分析虽然是一种先进的数学理论 ,但它跟博里叶变换一样，也仅仅是一种信号处理工具 ,在励磁涌流识别中的应用也只是作为一种工具 ,还是利用了励磁涌流的基本特点。

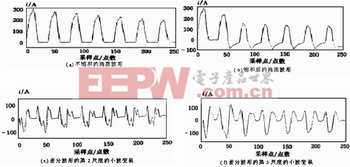
图1 非对称性涌流的饱和波形及其小波变换

小波变换的模局部极大值 ,即 | W₂^jf( x) |的局部极大值 ,对于检测信号的边缘和奇异性具有重要意义 。根据小波变换的局部极大值及其跨尺度传递 ,可准确地确定突变点的位置。本文利用小波分析的这一特性来提取变压器励磁涌流的间断角特征。

励磁涌流的小波变换特征

微机的变压器保护处理一般是经 CT转变的二次侧电流。线性 CT不存在饱和问题 ,而实际运行中的 CT由于励磁电流很大且存在直流偏移 ,因而有可能出现饱和。CT饱和是困扰变压器差动保护原理的重要问题之一。非对称性涌流的数值比对称性涌流大很多。引起饱和的一个重要原因是原边电流中非周期分量的影响 ,本文主要考虑非对称性涌流的饱和问题。

本文分别给出了非对称性涌流和故障电流的饱和波形及小波变换，如图1、图2所示。

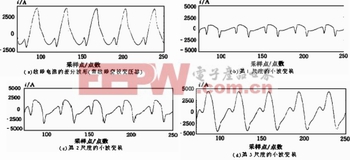
图2 变压器带故障空投时一次电流的差分波形机器小波变换

图 1、图 2中的小波变换模极大值与电流波形的奇异边界相对应，并沿尺度传递 ,为了去除高频噪声的影响 ,选取第 3尺度的小波变换的模极大值作为所提取的特征。对比非对称性涌流和短路电流的第3尺度的小波变换 ,即图 1(d)、图2(d) ,可见，故障电流的小波变换的模极大值是一正一负等间距出现的 ,而涌流的小波变换的相邻两模极大值是同号。这两个极大值对应于涌流波形的间断角。这一现象是由涌流的间断角导致的。可以利用这一特征来识别对称性涌流。

图 1给出了 CT饱和的仿真结果。图 1(b)是饱和后的单侧涌流 ,由于 CT严重饱和 ,因此，涌流波形的间断角已经不再存在。图 1(c)是对饱和后的波形进行差分后的波形。显然 ,差分后间断角有所恢复 ,但是差分也放大了高频分量。图1 (d)、 (e) 、( f)是对差分后CT饱和涌流波形的小波变换 1~ 3尺度的结果。从中明显看出 ,第 3尺度的小波变换不但具有前面所分析的相邻模极大值同号的涌流特征 ,而且滤除高频分量的效果很好。这说明前面得出的判据不受 CT饱和的影响。

图 2是故障电流的差分及其小波变换 ,这里考虑了最严重情况 (带故障空投变压器 ) ,此时波形的畸变很严重。但是故障电流差分后仍是没有间断角的准正弦波形 ,其第 3尺度的小波变换的模极大值仍是相邻异号。可以利用这一特征识别非对称性涌流和故障电流。

结语
本文提出了基于小波理论的区分励磁涌流和故障波形的新方法。利用小波理论进行特征提取 ,通过小波变换的模局部极大值提取励磁涌流的间断角特征 ,可定性地识别励磁涌流和内部短路。该原理对 CT饱和具有很强的鲁棒性 ,理论分析和仿真试验均表明该原理不受 CT饱和的影响。