高频变压器分布电容的影响因素分析
0 引言
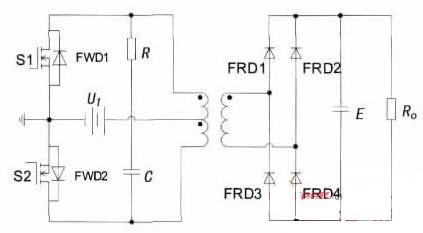
单端反激变换器具有拓扑结构简单,输入输出隔离,升降压范围宽,易于实现多路输出等优点,在中小功率场合具有一定优势,特别适合作为电子设备机内辅助电源的拓扑结构。变压器作为反激变换器中的关键部件,对变换器的整机性能有着很大影响。随着变换器小型化的发展趋势,需要进一步提高变换器的开关频率以减小变压器等磁性元件的体积、重量[1-3]。但高频化的同时,变压器的寄生参数对变换器工作的影响却不容忽视[4-12]。变压器的寄生参数主要是漏感和分布电容。以往,设计者在设计反激变压器时,往往只对变压器的漏感加以重视。然而,在高压小功率场合,变压器分布电容对反激变换器的运行特性及整机效率会有很大影响,不可忽视[8-13]。对设计者而言,正确的理解这些寄生参数对反激变换器的影响,同时掌握合理控制寄生参数的方法,对设计出性能良好的变压器,进而保证反激变换器高性能的实现颇为重要。为此,文中首先给出变压器寄生参数对反激变换器的影响分析,同时给出这些寄生参数的确定方法,并对变压器的不同绕法以及绕组布局对分布电容的影响进行了研究,对绕组分布电容及绕组间分布电容产生的影响作了分析,最后进行了实验验证。1 变压器寄生参数对反激变换器的影响如图1,给出考虑寄生参数后的高压输入低压输出RCD 箝位反激变换器拓扑。其中,Ll、Lm 分别表示原边漏感和磁化电感,C11 为原边绕组分布电容,C13、C24 表示原边与副边绕组不同接线端之间的分布电容。根据反激变换器的工作原理,反激变压器铁心工作于单向磁化状态,且需要一定的储能能力。为防止铁心饱和,通常在变压器磁路中留有较大气隙,但这会使得变压器有较大漏磁,造成较大的漏感。当功率开关管关断时,由于漏感的存
在,会在开关管上激起很高的电压尖峰[12-14]。漏感能量吸收方法有多种,图1 电路是采用RCD 箝位

路来吸收漏感能量,控制开关管关断电压尖峰。另外,在变压器中,绕组线匝之间、同一绕组上下层之间、不同绕组之间、绕组对屏蔽层之间沿某一线长度方向的电位是变化的,这样形成的变压器分布电容与静电容不同,其模型十分复杂[15-20]。为便于工程分析,通常与漏感在一起,采用图1 中所示变压器模型。在低压高功率场合,因分布电容中储存的电场能量(CU2/2)与漏感中储存的磁场能量(LI2/2)相比较小,因而分布电容的影响可以忽略。但在高压小功率场合,分布电容储能与漏感储能相当,甚至比漏感储能大,此时分布电容的影响不可忽略。
在开关转换时,绕组电压发生变化,在变压器内部和主电路回路中引起高频振荡,增加变压器的损耗,并产生高频电磁辐射,同时也会增加功率器件的动态功耗,引起较高的应力,成为损坏功率器件的隐患。若输入电压较高,分布电容储能较大,会使得开关管在转换时出现较大的电流尖峰,在采用峰值电流控制的情况下,将影响电流采样的正确性,在轻载时会对电源的稳压精度、稳定性及损耗
有较大影响。由于空间位置的不同,一般情况下,C13 和C24并不相等,与绕组绕制方式有关。如果变压器绕制时原副边绕组接触面集中于2 点和4 点,则C24 大于C13,反之亦然。若4 点接地时,电容C13 和C24两端电压变化对其充放电会引起功率损耗。
由此,为了保证变压器具有良好的高频特性,必须明确影响其寄生参数(包括漏感和分布电容)的因素,从而对其进行有效的控制。为避免反复试凑,在设计制作变压器之前,需要一种有效的方法来计算或估计出这些寄生参数的大小。这里给出了一种分析比较变压器漏感、绕组分布电容和绕组间分布。
2 寄生参数的确定
2.1 漏感
漏感表示变压器绕组之间不完全耦合所表现出来的寄生效应。耦合系数小于1 表示变压器绕组的空隙中存在漏磁场,漏感大小可以通过计算储存在绕组间的漏磁场能量来确定。可以认为这些漏能量等效于储存在一个集中表示的漏感中,这个漏感就可由下式计算得到:
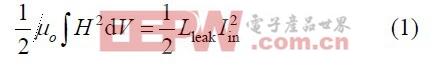
式中:式中:μo 为真空磁导率;H 为漏磁场强度分布;dV为漏磁场分布的体积元;Lleak 为变压器线圈漏感;Iin 为输入电流。
对变压器中的绕组分布作平面假设,可以得到变压器的磁场图。图2 给出了2 个实例,在导体部分磁场强度增加或减少,在层与层间的空间内磁场强度保持不变。

因磁场能量正比于H 的平方,采用交错绕法时Hm 会比较小,由此对漏感的影响也比较小,所以通常采用交错绕法以减小漏感。
2.2 绕组分布电容
绕组分布电容对应着变压器绕组中存储的电场能量。为了计算电场能量,需要知道变压器绕组中的电压分布。根据下式,可近似得到2 层绕组分布电容C11 的大小:

lm 是绕组导线平均长度;d 是绕组上下层间距;h 是绕组高度;E 是绕组间的电场强度;v 是上下层相邻层间的电压分布;Uin 是输入电压;ε是层间绝缘材料介电常数。由式(2)可见,通过公式变换,用电场分布的体积积分来表示的电场能量可表示为变压器中电压分布的线积分。而电压分布可以通过以下方法获得:在所测绕组上施加一个电压U,其余绕组开路,
假设这个电压沿着绕组长度方向均匀分布,从绕组一端电位为零开始,至另一端电位增长到U,这样即可获得绕组电压分布情况。图3 给出了不同绕法时的绕组电压分布。

可见,采用C 型绕法,绕线虽简单,但上下层相邻匝间的最大电压差大,分布电容储存的能量就很大,从而绕组的端口等效电容较大;采用Z 型绕法,绕线稍复杂些,但线圈上下层相邻匝间压差变小,绕组的端口等效电容明显减小。若要进一步减小绕组分布电容,则可采用分段骨架的方法或累进式绕法。分段骨架的方法是将原来的线圈匝数分成相等的若干份,线圈间的最大电压差就只有输入电压的若干分之一,分段越多,线圈间的最大电压差越小,绕组等效分布电容就越小。所谓累进式绕线方法,就是先绕第1 层的一部分,再在第1 层上绕回去,形成第2 层的一部分,这样交替绕制第1 层线圈与第2 层线圈,设累进的圈数为n,则线圈间的最大电压就是1/n。一般来讲,减小分布电容的绕制方法都可以减小导线间的绝缘应力。一个2 层绕组的线圈,如分别采用上述4 种绕法,累进式绕法减小绕组分布电容的效果最佳,两段式绕法次之,C 型绕法最差,Z 型绕法介于中间。以上给出了不同绕法时2 层绕组分布电容的比较,若匝数较多,绕组绕成更多层结构,总的绕组分布电容仍可由式(2)求出,只是此时的储能应是所有的储能之和。
2.3 绕组间分布电容
绕组间的分布电容可从电容的基本定义推导而得。这个电容是沿着绕组分布的,可以把原副边绕组看成2 根半径为a 的平行导线A、B,中心相距d,如图4 所示。

假设原边绕组、副边绕组分别携带电荷q、−q,距离A 的中心x 处P 点的电场强度为E,则场强E为导线A、B 的电荷分别在P 点产生的电场强度EA和EB 的叠加。根据高斯定理:

方向是由A 指向B。因此,A、B 间的电位差UAB 为:

由此可得长为l 的绕组间分布电容为:
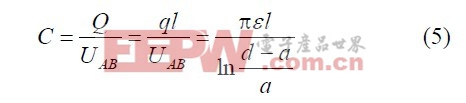
式中:ε 为绕组导体间绝缘材料的介电常数;l 为2绕组正对的平均长度。若绕组采用的是条状铜箔,如平面变压器绕
组,则2 个绕组间的电容可使用2 块平行导电板之间的电容计算公式直接求得:

变压器寄生参数的大小与绕组结构及绕组布局有很大关系,通过上述分析,可以得到以下结论:
(1)减小漏感可以由初级与次级绕组间的紧耦合来实现,也就是绕组结构上采用很小的间距以及布局上采用交错绕制的方法即可减小漏感。
(2)绕组采用不同的绕制方法,绕组分布电容差异较大。采用交错绕制方法,同一绕组层与层的实际间距增大了,所以绕组分布电容相应减小。
(3)绕组间分布电容除了与线圈层间距、层间绝缘材料以及绕线粗细有关外,与两绕组正对的面积有很大关系。因而,采用不同的绕组布局时,绕组间电容会有很大不同。采用交错绕制后,原副边绕组正对的面积变大,致使绕组间产生大的寄生电
容。紧密绕组的低漏感和大寄生电容成了一对矛盾。







评论