基于FPGA和Quartus II的程控滤波器测量系统的设计方案

1.引言

放大器和滤波器是现代电子系统的重要组成部分，其性能指标的优劣直接决定整个系统的性能。传统的放大器和滤波器大部分是固定放大倍数和固定的截止频率。在许多工程领域中，信号频率范围是动态的，约在几Hz到几十KHz之间，若按最大信号带宽下选择运算放大器的性能，会造成在较低信号频率下功耗浪费，因此需要可变截止频率的滤波器进行滤波。

本系统利用运算放大器、FPGA、D/A和LCD等核心器件设计程控滤波器和扫频测试仪，其中扫频测试仪可用于对滤波器的测试。输入为mV级信号，电压增益60dB,10dB可调，误差小于2%.高通、低通滤波器的截止频率在1kHz~30kHz,1kHz可调，误差小于2%.

2.系统结构设计与理论分析

2.1 系统结构框图

本系统主要由可控放大电路、滤波电路、正弦信号产生电路和FPGA构成，其系统框图如图1所示。

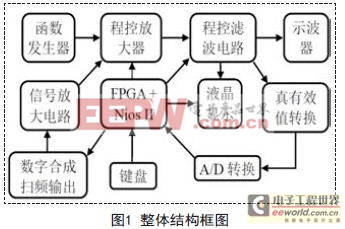
前级程控放大采用继电器来选择放大器的反馈电阻以实现不同的增益，滤波器采用电流型DAC构建传递函数实现，该方法便于控制而成本较低，正弦信号产生采用FPGA查找表的方法，能得理高精准的频率。控制核心采用NIOS,无需复杂的外路电路与FPGA进行通讯。

2.2 滤波器传递函数推导

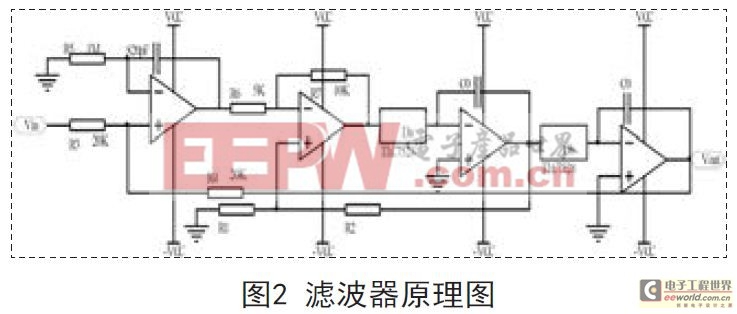
高通/低通滤波器的原理图如图2所示，根据放大器的“虚短虚断”原理，低通的传递函数近似为：

其中滤波器的Q值为：

为得到平坦的巴特沃兹滤波器，则当Q=0.707时所对的ω即为低通截止频率。

此时有NB与fc成正比，NB为正数，为得到截止频率从1K到 ,则fc=1000NB/8,当NB=240时，fc=30KHz.选择C0=820pF,此时有(R1+R2)/R1=1.225,取R1=20KΩ，R2=4.5KΩ。

2.3 扫频测试原理在F P G A中的R O M导入1 2位的正弦数表， 共4 0 9 6 个点， 共有1 2 根地址线，FPGA的晶振为50MHz,通过锁相环倍频到200MHz,通过累加器输入频率控制字和相位控制字，控制查找表的速度，来实现不同频率的输出。

通过编程改变频率控制字，从而改变输出频率。系统对每一个不同频率的频点进行测量，经过A D 6 3 7将交流转换为直流后，通过TI公司的模数转换芯片ADS7886,将有效值送入处理器，并通过扫频的点绘制相应的曲线，得到频幅响应曲线。

3.硬件电路与软件实现

3.1 程控放大器

为得到很高的增益，采用两级放大器级联的方式来实现。用FPGA给74HC595发送控制字来控制继电器的开合，选择放大器的不同的反馈电阻，以实现不同的增益放大。图3所示为程控放大器的连接电路图。

每一级增益分配为0 d B 、1 0 d B 、20dB、30dB,通过模拟开关同时控制两级增益，可以使总体增益分别为0 d B、10dB、20dB、30dB、40dB、50dB和60dB.

其中调节R9和R10可以抑制失调电压。