相位噪声是什么
1概述
本文引用地址:http://www.amcfsurvey.com/article/227558.htm定义
相位噪声和抖动是对同一种现象的两种不同的定量方式。在理想情况下,一个频率固定的完美的脉冲信号(以1 MHz为例)的持续时间应该恰好是1微秒,每500ns有一个跳变沿。但不幸的是,这种信号并不存在。实际信号的信号周期的长度总会有一定变化,从而导致下一个沿的到来时间不确定。这种不确定就是相位噪声,或者说抖动。
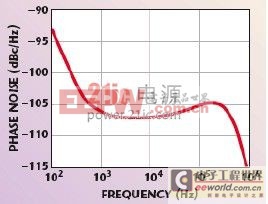
频域概念
相位噪声是对信号时序变化的另一种测量方式,其结果在频率域内显示。用一个振荡器信号来解释相位噪声。如果没有相位噪声,那么振荡器的整个功率都应集中在频率f=fo处。但相位噪声的出现将振荡器的一部分功率扩展到相邻的频率中去,产生了边带(sideband)。从图2中可以看出,在离中心频率一定合理距离的偏移频率处,边带功率滚降到1/fm,fm是该频率偏离中心频率的差值。
相位噪声通常定义为在某一给定偏移频率处的dBc/Hz值,其中,dBc是以dB为单位的该频率处功率与总功率的比值。一个振荡器在某一偏移频率处的相位噪声定义为在该频率处1Hz带宽内的信号功率与信号的总功率比值。2 相位噪声表征
一个理想的正弦波信号可用下式表示:
V(t)=A0sin2πf0t (1)
式中,V(t)为信号瞬时幅度,A0为标称值幅度,f0为标称值频率。此时信号的频谱为一线谱。但是由于任何一个信号源都存在着各种不同的噪声,每种噪声分量各不相同,使得实际的输出成为:
V(t)=[A0+ε(t)]sin[2πf0t+j(t)] (2)
在研究相位噪声的测量时,由于考虑振荡器的幅度噪声调制功率远小于相位噪声调制功率,所以 ε(t)
V(t)=A0sin[2πf0t+j(t)] (3)
对j(t)的测量,可以用各种类型的谱密度来表示。显然此时的相位起伏为Δj(t)=j(t),频率起伏为Δf(t)=[dj(t)/dt]/2π。常用的相对频率起伏:
y(t)=[dj(t)/dt]/2πf0 (4)
由于相位噪声j(t)的存在,使频率源的频率不稳定。这种不稳定度常用时域阿仑方差σ2y(2,τ,τ)及频域相对单边带功率谱(简称功率谱)Lp(f)或相噪功率谱Sj(f)来表征。它们的定义为:
σ2y(z)=σ2(2,τ,τ)=(1/v20)(1/2)(y1-y2)2 (5)
式中y1,y2为测量采样时间τ的相邻二次测量测得的频率平均值。Lp(f)=[PSSB(f)/P0](dBc/Hz) (6)
其中PSSB(f)为一个相位噪声调制边带在频率为f处的功率谱密度,P0为载波功率。
由(3)及(4)式得相位起伏的自相关函数Rj(τ)=[j(τ),j(t+τ)]和相对频率起伏的自相关函数Ry(τ)=[y(τ), y(t+τ)],由维纳-钦辛定理可知自相关函数和功率谱密度间存在如下关系
表示傅里叶变换对。通常j(t)1,近似有
Lp(f)=(1/2)Sj(f)[1](7)
3相位噪声产生原因
1,相位调制的方法:PSK,DPSK,DQPSK产生
2,相位噪声的起因:放大器噪声和非线性克尔效应,也即自相位调制(SPM)和交叉相位调制(XPM)和四波混频,但一般在分析的时候只考虑到SPM引起的相移效应。
3,相位噪声的统计特性;这是研究这方面的重点和难点,和其他的随机过程一样,非线性相位噪声和光强度也服从一定的联合概率分布。按照K.P.Ho的paper一般用特征函数来求其联合概率分布。其结论是,同激光的相位统计噪声不同,相位调制的相位噪声服从菲中心卡方分布和高斯随机分布的卷积(见Stastics of Noline phase Noise) 。
4,非线性相位噪声的补偿:线性和非线性,使用的是MMSE和MAP准则,同一般通信原理中的最小误码概率方法的一样。但其实现较困难的。5,以上考虑基本上没有考虑色散和PMD和DWDM中的效应,因此,在实际计算是应该考虑更多,但基本思想还是一样,就是利用概率来使信号的BER最小。
5 相位噪声的影响
接收机
电子技术的发展,使器件的噪声系数越来越低,放大器的动态范围也越来越大,增益也大有提高,使得电路系统的灵敏度和选择性及线性度等主要技术指标都得到较好的解决。随着技术不断提高,对电路系统又提出了更高的要求,这就要求电路系统必须低相位噪声,在现代技术中,相位噪声已成为限制电路系统的主要因素。低相噪对提高电路系统性能起到重要作用。



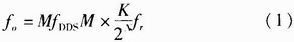


评论