Buck-Boost 稳态连续导通模式分析

介绍Buck - Boost的稳态连续导通模式分析,这部分主要目的就是给出一个Buck - Boost稳态连续导通模式下电压转换关系的推导。这是很重要的，因为它揭示了输出电压怎样由占空比和输入电压决定，或者相反，怎样基于输入电压和输出电压来计算占空比。稳态说明输入电压、输出电压、输出负载电流和占空比都是固定不变的，大写字母表示出了稳态下的变量名。

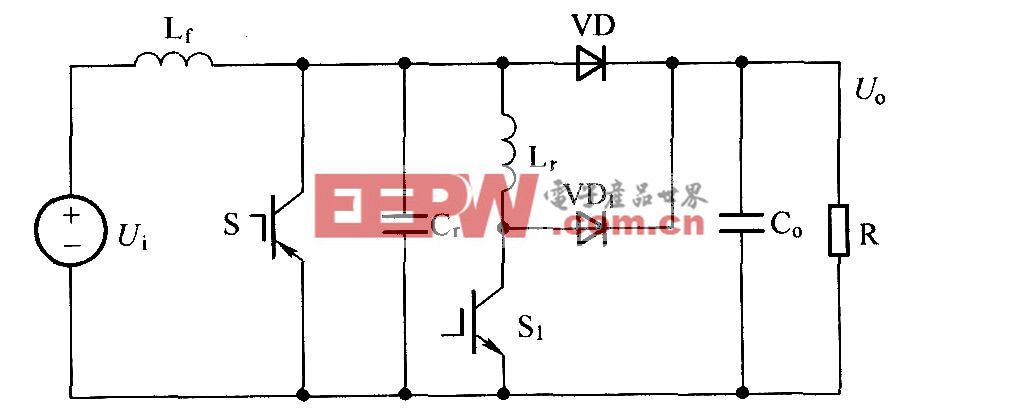
在连续导通模式，buck - boost转换器保证每个开关周期有两个功率态，当Q1是开、CR1是关时，就是开态（ON)；当Q1是关而CR1是开时,就是关态（OFF)。在每个状态中，当回路中的开关被等价回路所代替时，一个简单的线性回路可以用来表示这两种状态，两种状态的回路图表见图2.

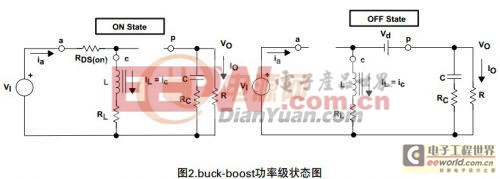
开态的时间为D×TS= TON，其中D为由控制回路设定的占空比，代表了开关在开态的时间占整个开关周期（TS）的比值。关态的时间叫TOFF，因为对于连续导通模式下在整个开关周期中只有两个状态，所以TOFF等于(1–D)×TS，数值（1–D）有时被成为D,这些时间与波形一起显示在图3中。

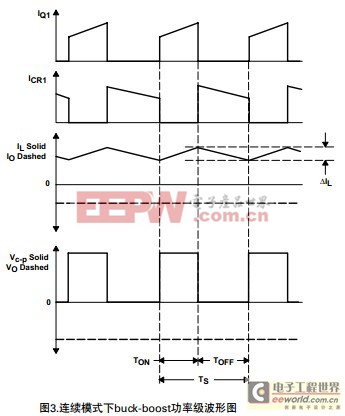
参考图2，在ON态，Q1此时为低电阻，RDS(ON)，从漏极到源极，只有很小的电压降VDS= IL×RDS(on)。同时电感器的直流电阻上的电压降也很小，等于IL×RL。因此，输入电压VI，减去损耗( VDS+ IL× RL)，就加载到电感器L两端。在这段时间CR1是关的，因为它是反向偏置的。电感电流IL，从输入源VI流出，经过Q1，到地。在开(ON)态，加在电感器两端的电压为定值，等于VI– VDS–IL×RL。通过改变图2中电流IL的极性，电感上的电流会随着所加的电压而增大。同时，由于加载的电压通常必须为定值，所以电感电流线性增加。图3描述了在TON时间内电感电流的增加。

电感电流的增加量可以由类似关系式来求得:

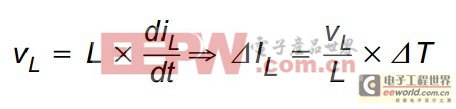
在开态（ON）时间内电感电流的增量由下式可得:

量ΔI(+)代表了电感的纹波电流，同时注意在此期间，所有的输出负载电流由输出电容C提供

参考图2，当Q1关时，它的漏极和源极间有很高的阻抗，所以，流过电感L的电流不能瞬时的变化，从Q1转移到CR1。随着电感电流的减小，电感两段的电压改变极性直到整流器CR1变为前向偏置，打开的时候，这时电感L两段的电压变为(VO–Vd–IL×RL)，式中的Vd是CR1的前向电压降。电感电流IL，这时从输出电容和负载电阻的组合，经过CR1到地。注意CR1的方向和电感中电流的流向意味着输出电容和负载电阻中电流导致VO为负电压。在关态（OFF）时，电感两端的电压为定数，且为(VO–Vd–IL×RL)，为了保证同样极性的转换，这个加载电压必须是负的（或者在开态（ON）时为极性相反的加载电压），因为输出电压为负的。因此，电感电流在OFF态时是减小的，而且由于加载电压必须是常数，所以电感电流线性减小。TOFF时间内电感电流的减小见图3.

在关态（OFF）电感电流的减小可以由下式求得:

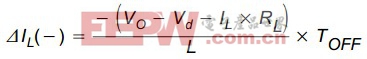
量ΔIL(–)也代表了电感的纹波电流。

在稳态条件下，开态（ON）下的电流增加量ΔIL( + )和关态（OFF）下的电流减小量ΔIL(-)必须是相等的。否则，在一个周期到下一个周期，电感电流就会有一个净的增加量或者减小量，这就不是一个稳态了。所以，这两个方程必须相等，从而求出VO，得到连续导通下buck - boost能量转换的关系式:

求解出VO:

用TON+TOFF来替换TS，并利有D = TON/TS和(1-D)=TOFF/TS，VO的稳态方程可变为:

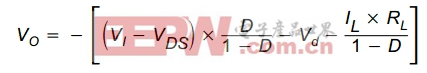
注意在上式的化简中，用到了TON+TOFF等于TS，这只是在连续导通模式下成立的，在我们以后分析到非连续导通模式下就可以看到。

我们还发现，ΔIL的两个值相互相等的假定，等同于电感上的电压-秒曲线的平衡。电感上的电压–秒关系是由加载在电感上的电压和加载电压的时间来确定的。这是用已知的电路参数来计算像VO和D等未知值的最好方法，这种方法在本文中将经常用到。电感上的电压-秒关系平衡在物理上是必须的，而且就像欧姆定律一样容易理解。

我们还发现，ΔIL的两个值相互相等的假定，等同于电感上的电压-秒曲线的平衡。电感上的电压–秒关系是由加载在电感上的电压和加载电压的时间来确定的。这是用已知的电路参数来计算像VO和D等未知值的最好方法，