单片机CRC快速算法
1 引言
CRC(循环冗余码)检验技术广泛应用于测控及通信领域。在很多情况下,CRC计算是靠专用的硬件来实现的,但是对于小型低成本的单片机系统来说,若要在没有这些硬件的支持下实现CRC检验,首先要解决的就是如何通过软件高效快速地完成CRC计算的问题,也就是CRC算法的问题。
这里将提供两种算法,它们稍有不同,一种适用于程序空间大一些的51系列等单片机,另一种适用于程序空间的使用条件十分苛刻的PIC单片机。这些算法按字节进行计算,仅使用查表和简单的异或运算等操作,所以,计算过程相当简捷,而计算速度却很快。
下面先简述一下CRC原理,然后再以CRC-CCITT标准生成多项式为例对算法进行说明,并给出一个51系列单片机子程序和一个PIC单片机子程序。
2 CRC原理
CRC检验原理实际上就是在一个p位二进制数据序列之后附加一个r位二进制检验码(序列),从而构成一个总长为n=p+r位的二进制序列,例如,p位二进制数据序列D=[dp-1dp-2 ......d1d0],r位二进制检验码R=[rr-1 rr-2....r1 r0],所得到的这个n位二进制序列就是M=[dp-1dp-2 ......d1d0 rr-1 rr-2....r1 r0]; 附加在数据序列之后的这个检验码与数据序列的内容之间存在着某种特定的关系。如果因干扰等原因使数据序列中的某一位或某些位发生错误,这种特定关系就会被破坏,因此,通过检查这一关系, 就可以实现对数据正确性的检验。
校验码R是通过对数据序列D进行二进制除法取余式运算得到的,它被一个称为生成多项式的(r+1)位二进制序列G=[gr gr-1 .... g1 g0]来除,用多项式形式表示为
![]()
(1)
其中,xrD(x)表示将数据序列D左移r位(即在D的末尾再增加r个0位),Q(x)代表这一除法所得的商,R(x)就是所需的余式。这一运算关系还可以用式(2)来表达 ![]()
(2)
其中,Re[ ]表示对括号内的式子进行取余式运算。 检验码的编码计算如上所述,而检验过程则是对M序列直接进行除法取余式运算,即
![]()
(3) 或表示为
![]()
(4) 所得到的余式R(x)若为零则表示数据正确,否则认为发生错误。
3 快速算法的基本思路 这里仅以CRC-CCITT标准生成多项式为例进行说明。CRC-CCITT是一个17位生成多项式G=[1 0001 0000 0010 0001],用多项式形式表示为G(x)=x16+x12+x5+1,由它产生的检验码R的二进制位数是16位(2字节)。 单片机的操作是以字节形式进行的,所以,算法应以字节为单位进行运算。这里将把用字节构成的二进制序列称为“字节序列”,显然,单片机的数据序列、检验码以及它俩组成的序列M都是字节序列,或者说是“多字节序列”。 实际上,这种算法所要解决的问题就是如何对多字节序列进行除法取余式运算的问题。3.1 多字节序列运算规律 首先设一个由i个字节 m1、m2、......、mi-1、mi 构成的8×i位二进制序列,并用字节形式表示它为Mi =[ m1 m2 ...... mi-1 mi ],然后再截取Mi的前(i-1)个字节构成一个Mi-1序列,Mi-1=[ m1 m2 ...... mi-1 ],这两个序列之间的关系可以用多项式表示为Mi(x)=x 8Mi-1(x)+mi(x),其中,mi(x)是字节mi的二进制多项式表示形式,而x8Mi-1(x)表示将Mi-1序列左移一个字节。 对于序列Mi-1来说,
![]()
(5)
其中,二字节序列余式Ri-1=[hi-1 li-1]。 而对于Mi序列来说,可得 ![]()
(6) 这一结果的前一项为一整数,所以它与余式无关,这样,余式只可能出现在后一项中。因此,对x8Ri-1(x)+mi(x)取余式运算就等价于对Mi(x)的取余式运算,用式(4)的形式表示为 ![]()
(7) x8Ri-1(x)+mi(x)代表一个由Ri-1和mi共同组成的三字节序列[ hi-1 li-1 mi],而且对这个三字节序列的取余式运算就等于对Mi序列的取余式运算,其结果就是Mi序列的余式Ri=[ hi li ]。同理可得,对于一个Mi+1序列(它比Mi序列多一个字节mi+1)来说,对三字节序列[ hi li mi+1]的运算就等价于对Mi+1序列的运算,其结果就是Mi+1序列的余式Ri+1=[ hi+1 li+1 ]。 显然,这反映出一种如图1所示的递推运算的规律。可见,每一次递推运算都是对一个三字节序列的计算,所以,如何简单快捷地对三字节序列进行计算是这种算法的又一个关键。
单片机相关文章:单片机教程
单片机相关文章:单片机视频教程
单片机相关文章:单片机工作原理



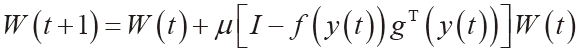






评论