循环冗余校验码---CRC码

　　CRC码一般是指k位信息码之后拼接r位校验码。应用CRC码的关键，是如何从k位信息位简便地得到r位校验位(编码)的值，以及如何判断k+r位的码字是否正确。下面仅就CRC码应用中的问题做简单介绍(有关的理论问题请参阅有关书籍)。

① CRC码的编码方法

　　先介绍CRC码编码用到的模2除运算。

　　模2运算是指以按位模2相加为基础的四则运算，运算时不考虑位间进位和借位。

　　模2加减：即按位加,可用异或逻辑实现。模2加与模2减的结果相同,即
　　　　0±0=0 0±1=1 1±0=1 1±1=0。两个相同的数据的模2和为0。

　　模2乘：按模2加求部分积之和。
　　例: 　　　1010
　　　　 　　　101
　　　　　
　　　　　　　1010
　　　　　　 0000
　　　　　　1010
　　　　　
　　　　 　 100010

　　模2除：按模2减（加）求部分余数。每求一位商应使部分余数减少一位。
　　上商的原则是：当部分余数的最高位为1时，该位商取1；为0时，该位商取0。当部分的余数的位数小于除数的位数时，该余数即为最后余数。
　　例如，

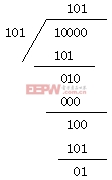
　　下面介绍CRC码的编码方法。
　　首先,可将待编码的k位有效信息位表达为多项式M(x)形式:
　　　　M(x)= C_k-1x^k-1 + C_k-2x ^k-2+…+C_ixⁱ+…+C₁x¹+C₀
　　式中C_i为0或1，x为伪变量，并用xⁱ指明各位间的排列位置。

　　若将信息位组左移r位,则可表示为多项式M(x) * x^r ,这样就可以空出初值为０的r个校验位，即
　　　　　　

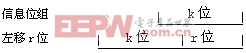
　　CRC码的码字，是用k个数据位拼接上r个校验位得到的。校验位的值，就是通过对多项式M(x) * x^r除以生成多项式G(x)(特定的一个多项式)所得到的余式。为了得到r位余数(校验位)，G(x)必须是r+1位的，即为r次的多项式。
设所得余数表达式为R(x),商为 Q(x)，就有：
　　　　　M(x).x^r / G(x) = Q(x) + R(x) / G(x)

　　将r次余式直接拼接在源数据多项式的右侧，可写成M(x).xr + R(x)，并可推导出：
　　　　　M(x).x^r + R(x) = [ Q(x)* G(x) + R(x) ] + R(x)
　　　　　　　　　　　　 = [ Q(x)* G(x) ] + [ R(x)+R(x) ]
　　　　　　　　　　　　 = Q(X)* G(x)

　　这证明所得到的CRC码字是一个可被G(x)（多项式）数码除尽的数码（多项式）。
　　例：对四位源信息 1100，来求三个校验位的值，可选择生成多项式为 1011，则有：
　　　　 M(x) = x³ + x² = 1100 　　　(k = 4)
　　　　 M(x)*x³ = x⁶ + x⁵ = 1100000 (左移， r = 3位)
　　　　 G(x) = x³+ x + 1 =1011 　　 (r+1 = 4位)

　　

　　所得到的码字（系统线性（7,4）分组码）为：
　　　　 M(x).x³ + R(x) = 1100000 + 010 = 1100010