一阶电路的零状态响应

当所有的储能元件均没有初始储能，电路处于零初始状态情况下，外加激励在电路中产生的响应称为零状态响应。

下面分别讨论激励为直流、正弦交流情况下，、电路的零状态响应。

一、直流激励下的零状态响应。

1、串联电路

如图8-5-1所示，开关S原置于位置2，电路已达稳态，即，电容上无初始储能。在时刻，开关S由2切换至1，电路接通直流电压源，求换路后的零状态响应、、。

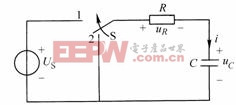
图8-5-1

当，开关S切换至1，由得：

（式8-5-1）

这是一个一阶线性常系数非齐次微分方程。由微分方程求解的知识得，特解：

齐次方程的通解：

全解为：

（式8-5-2）

根据换路定则：

由（式8-5-2）：

因此：

最终求得：

（式8-5-3）

（式8-5-4）

（式8-5-5）

根据（式8-5-3）—（式8-5-5），画出零状态响应、与随时间变化的曲线，如图8-5-2所示。

图8-5-2

在图8-5-1所示电路中，当后，电压源对电容充电。电容从初始电压为零逐渐增大，最终充电至稳态电压，而电流则从初始值逐渐减小，最终衰减至稳态值零。

2、串联电路。

如图8-5-3所示，开关S置于位置2，电路已达稳态，即，电感L上无初始储能。在时刻，开关S由2切换至1，电路接通直流电压源，求换路后的零状态响应、和。

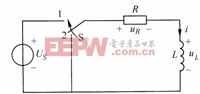
图8-5-3

当后，开关S切换至1，由得：

（式8-5-6）

（式8-5-6）是一个一阶线性常系数非齐次微分方程。该方程的全解是特解和齐次方程的通解之和，即：

（式8-5-7）

表示全解，表示特解，表示通解。换路后电路达到新的稳定状态的稳态电流就是特解，即：

（式8-5-8）

其通解为：

（式8-5-9）

于是，全解为：

（式8-5-10）

（式8-5-10）中的积分常数A由初始条件确定。在时刻，根据换路定则：

由（式8-5-10）：

因此：

最终得到：

（式8-5-11）

（式8-5-12）

（式8-5-13）

显然，，满足。图8-5-4绘出了零状态响应、和的曲线。

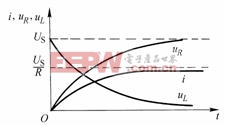
图8-5-4

二、正弦交流激励下的零状态响应

1、串联电路

仍以图8-5-1所示电路为例，将直流电压源改为正弦交流电压源，当后，由得到电路的微分方程为：

（式8-5-14）

的全解等于特解和通解之和，即：

由于激励是正弦交流激励，即为稳态分量，即为暂态分量。稳态分量可利用相量计算：

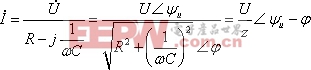
式中 ：

暂态分量仍为，于是全解为：

（式8-5-15）

当时刻，根据换路定则，确定积分常数：

由（式8-5-15）：

最终得到：

（式8-5-16）

（式8-5-17）

（式8-5-18）

（式8-5-16）～（式8-5-18）说明电源的初相角对暂态分量的大小有影响，通常称为接通角。当或时，电容电压的暂态分量为最大。从（式8-5-16）不难看出，电容过渡电压的最大值无论如何不会超过稳态电压幅值的两倍。但是从（式8-5-17）可以看出，在某些情况下，过渡电流的最大值将大大超过稳态电流的幅值。

2、RL串联电路

仍以图8-5-3所示电路为例，将直流电压源改为正弦交流电压源，当后，由KVL得到电路的微分方程为：

（式8-5-19）

初始条件仍是。如前所述，非齐次微分方程的全解是特解与通解之和，即：

（式8-5-19）右边是正弦函数，特解也是正弦函数，特解就是正弦交流激励下的稳态电流，可用相量求解：

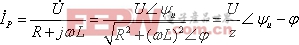
式中：

，

（式8-5-20）

暂态电流仍为：

（式8-5-21）

于是全解为：

（式8-5-22）

根据换路定则：

由（式8-5-22）：

因而：

最终得到：

（式8-5-23）

（式8-5-24）

（式8-5-25）