对称三相电路中的高次谐波

在实际的电力系统中，三相发电机产生的电压往往不是理想的正弦波。电网中变压器等设备由于磁路的非线性，其励磁电流往往是非正弦周期波形，包含有高次谐波分量。因此在三相对称电路中，电网电压与电流都可能产生非正弦波形，即存在高次谐波。下面分析对称三相电路中（电路负载为三相对称线性负载，电源为三相对称电动势）高次谐波情况。

非正弦三相对称电动势各相的变化规律相似，但在时间上依次相差三分之一周期，取A相为参考起点，则三相电动势为：

（6-3-1）

由于各相电动势为非正弦周期量，可把它们展开为傅里叶级数。一般情况下，发电机的三相电动势均为奇谐波函数，只包含奇次谐波分量。对于各相展开式有：

即：

同理有：

由上述三相电势表达式可见，基波、7次谐波分量各相振幅相等，相位差各为，相序变化依次为A→B→C→A，因此构成正序对称三相系统。可推得次谐波分量都组成正序对称三相系统。

各相中5次谐波分量振幅相等，相位各差，但相序变化次序为A→C→B→A，故构成对称三相负序系统。可推得次谐波均组成负序系统。

各相中三次谐波分量振幅相等、相位相同，这样的三相系统称为对称零序三相系统。可知次谐波均构成零序系统。这样三相非正弦周期对称电动势中的各个同频率分量可分成正序，负序和零序三个不同的系统。

下面分析对称非正弦三相电路的求解方法，先来看在Y－Y无中线连接方式时相电压与线电压的关系。如果电源相电压中含有高次谐波，由于线电压为二个相电压之差，如，由前面各相展开式不难看出，对于正序和负序系统的各次谐波分量，其线电压有效值是对应相电压分量有效值的倍，而对于零序分量，由于其幅值相等相位相同，在线电压中将不包含这些谐波分量。因此对于电源相电压有效值有：

而线电压有效值为：

对于Y－Y有中线系统，如图6-3-1所示电路，在基波分量激励时，电路的计算方法已在第四章对称三相正弦电路中作过详细讨论，由于中性点电位，计算时可采用单相图求得A相电压电流值，然后直接写出B、C相的电压电流值。此时中线电流为零。同理凡是正序系统的各次谐波，均可用这种方法计算。

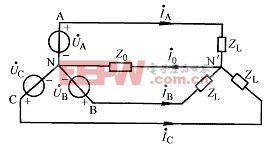
图 6-3-1

对于负序系统的五次谐波分量，其中性点电压：

因此仍然可以采用与基波分量相同的单相图计算，当得出A相电压电流后，依次写出B、C相电压电流，只是需注意相序为A→C→B，即C相滞后A相，B相滞后C相。

对于三相三次谐波电势，有，令，，中性点电压为：

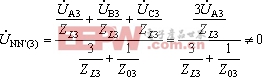
即中性点电压不为零，它包含有三次谐波分量。可计算负载A相三次谐波电流为：

可见在计算A相三次谐波电流时，A相电路等效阻抗为，即包含一个3倍中线阻抗的附加阻抗值。据此可作出计算三相三次谐波的单相计算图（见图6-3-2）。其余二相的电压电流与A相完全相同。中线电流是相电流的三倍。零序系统中其余谐波分量的计算方法与此相同。

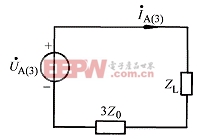
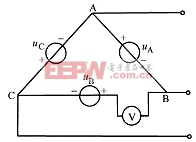
图 6-3-2 图 6-3-3

对于Y－Y联结无中线电路，由于零序分量的各相电压大小相同相位相同，尽管中点间电压不为零，但无零序分量电流。因此负载相电流与相电压均不包含零序谐波分量。对于负载接成三角形的Y－△联结电路，由于相电压等于线电压，而线电压中不包含零序分量，因此负载相电压相电流不含零序分量，线电流中也不含零序分量。

下面分析非正弦周期三相电源接成三角形的情况。如图6-3-3所示，在△联结中串入一电压表，则可知在表两端的瞬时电压为：

其有效值为：

△联结的环路中存在电动势，会在环路中产生对应的谐波电流。由于三相电源的内阻一般都很小，因此即使是较小的零序谐波分量也会产生一个很大的谐波电流。电源内部的环流会增加发电机绕组损耗，降低发电机效率，使电机过热，不利于机组运行。因此一般情况下三相发电机绕组不采用△联结方式。进一步分析可知，在△联结的三相电源中，环流在每相绕组内阻抗上的压降等于该相零序电动势的值，且方向相反，故△联结的电源线电压中不包含零序分量，可推知△－△联结的电路系统中负载上也不包含零序电压电流分量。