太阳能电池阵模拟器设计方案
太阳能发电一种新兴的可再生能源。目前,在航天电源领域内,绝大多数卫星电源均使用太阳能
卫星的空间工作条件恶劣且复杂,温度范围大,日照条件变化迅速,且太阳能电池方阵处于高能粒子辐射下,在地面上无法采用实际的太阳能电池方阵来再现卫星在空间轨道中的工作状态,因此需要采用太阳能电池
2 太阳能电池的数学模型
根据太阳能电池原理和图1 所示的实际测量结果建立了多种模型,用于太阳能电池的测试和应用研究。事实证明,这些模型具有足够的工程精度。
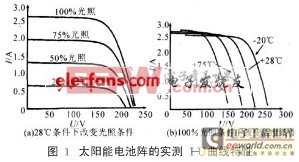
2.1 单指数模型
图2 示出太阳能电池的等效电路。

Iph 取决于太阳能电池各工作区的半导体材料性质和电池几何结构参数以及入射光强、表面反射率、前后表面复合速度、材料吸收系数等。由于器件的瞬时响应时间相比于绝大多数光伏系统的时间常数显得微不足道,因此分析中可忽略结电容。设定图中所示的电压、电流为正方向,由固体物理理论和全电路欧姆定律即可推出目前常用的单指数形式的太阳能电池模型:

式中:I0———二极管反向饱和电流;q———电子电荷;I———电池的输出电流;K———波尔兹曼常数;T———绝对温度;A———二极管品质因子(曲线因子),一般A=1~2:
2.2 双指数模型
在单指数模型中,在不同的电压范围内,决定IVD 的因素也不同。当电压较高时,IVD 主要由电中性区的注入电流决定;当电压较低时,IVD 主要由空间电荷区的复合电流决定。为了提高模型精度,可以综合考虑这两种情况,在等效电路中用两个参数不同的二极管来产生这两个电流,如图3 所示。
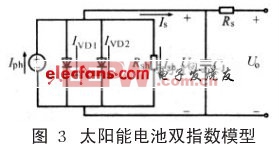
两个二极管产生的暗电流IVD1,IVD2 可分别表示成一个指数式的形式,这就是双指数太阳能电池理论模型,其表达式为:

式中:I01,A1———电中性区的饱和电流及完整性因子;I02,A2———空间电荷区的饱和电流及完整性因子
该模型不仅考虑了Rs 和Rsh 对太阳能电池性能的影响,而且用指数的形式概括地表示了不同机制下产生的IVD,并将不同电压范围内的IVD 决定因素也考虑在内,因而具有更高的精度。
2.3 工程应用的模型
上述单指数和双指数模型是基于物理原理的最基本的解析表达式,已被广泛应用于太阳能电池的理论分析中。但由于表达式中的参数,包括Iph,I0(或I01,I02),Rs,Rsh 和A(或A1,A2)与电池温度和日射强度都有关,确定起来十分困难,因此不便于工程应用,在太阳能电池供应商向用户提供的技术参数中也不包括这些参数。
工程用模型强调的是实用性与精确性的结合。
实际应用中,在设计各种系统时,考虑到数字仿真和模拟时的动态反应速度及计算工作量,必须尽可能在工程精度允许的条件下简化模型。
工程用太阳电池的模型通常要求仅采用供应商提供的几个重要技术参数,如短路电流Isc、开路电压Uoc、最大功率点电流Im、最大功率点电压Um、最大功率点功率Pm,就能在一定的精度下复现阵列的特性,并便于计算机分析。
鉴于单指数模型已足以精确描述太阳能电池的伏安特性,下面将在单指数模型的基础上,通过忽略(U+IRs)/Rsh 项和设定Iph=Isc,得到工程实用的太阳能电池模型。忽略(U+IRs)/Rsh 项,是因为在通常情况下Rsh 较大,有几百到几千欧,该项远小于光电流;设定Iph=Isc,是因为在通常情况下Rs 远小于二极管正向导通电阻。
此外,定义:
①开路状态下,I=0,U=Uoc;
②最大功率点时,U=Um,I=Im。
据此,太阳能电池的I-V 方程可简化为:
![]()
在最大功率点时,U=Um,I=Im,可得:
![]()
由于在常温条件下exp[Um/(C2Uoc)])1,因此可忽略式中的“- 1”项,解出:
![]()
注意到开路状态下,当I=0 时,U=Uoc,于是有:
![]()
可见,该模型只需输入太阳电池通常的技术参数Isc,Uoc,Im,Um,即可求出C1 和C2。从Isc,Uoc,Im,Um的变化中可体现出光照强度和电池温度的变化。工程应用中可通过实测曲线来设置这4 个参数,亦可通过近似的函数来描述这组参数的变化。通常可近似认为Isc,Uoc 分别随温度和光照强度呈线性变化。










评论