低频谐波失真度仪设计
目前,测量失真度的仪器根据测量原理大致可分为二大类:基波剔除法和频谱分析法。一般模拟式的失真度测量仪都采用基波剔除,这种仪器测量的误差较大;而频谱分析法,则是利用频率分析仪测量各次谐波的含量并计算出波形失真度的方法。它可分析测量出被测信号中的1~10次谐波分量。采用该方法较好地解决了超低频率失真度的测量,缺点是仪器结构复杂,价格较贵,操作繁琐。
1 测量原理
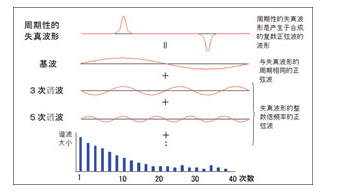
一个失真的周期振荡信号电压,除有基波电压分量外,还有各次谐波分量存在,把周期失真的正弦信号展开成傅立叶级数,可表示为:

其中,f(t)是一含有谐波失真的正弦波,A0= 上式中,A0/2为正弦波中直流分量,An为第n次谐波的振幅,n为失真正弦波中所含最高谐波次数,ω0为标准正弦波的角频率,φn为第n次谐波相对于基波的初相角。
上式中,A0/2为正弦波中直流分量,An为第n次谐波的振幅,n为失真正弦波中所含最高谐波次数,ω0为标准正弦波的角频率,φn为第n次谐波相对于基波的初相角。
一般地,正弦波的失真是用失真度,即所有谐波能量之和与基波能量之比的平方根来表示的:

数为n次的失真度,只要求出各次谐波的幅值,就可计算出信号的失真度。在实际测量中由于实现困难,模拟失真度仪测量所测出的数值是各谐波电压有效值和总的电压有效值之比,
即

模拟失真度仪的原理框图如图1所示。

被测信号经过放大器后,首先直接进入电子电压表,测出其总电压的有效值,并调至100。然后,信号通过滤波器,滤去基波成分,再次进入电子电压表,测出剔去基波后电压的有效值,此时指示即为失真度。显然,它只是失真度的近似值,必要时必须进行补偿。 基于FFT的失真度仪,采用频域分析方法,通过计算傅立叶系数,C1、C2…Cn,最后得到失真度大小。
由失真度定义得:
基本方法就是通过傅立叶变换(FFT),产生出信号的频谱图,根据频谱含量的大小Cn,计算出失真度。此类分析需要频谱分析仪和同步示波器。本文提出一种由虚拟仪器实现的、基于FFT的失真度测量,该失真度测量仪硬件原理如图2所示。






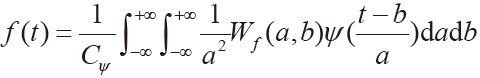



评论