频率特性又称频率响应,它是指系统或元件对不同频率的正弦输入信号的响应特性。系统的频率特性可由两个方法直接得到:(1) 机理模型—传递函数法;(2) 实验方法。 5.1.1 由传递函数求系统的频率响应
设系统的开环传递函数 对应的频率特性为 如果在S平面的虚轴上任取一点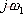 ,把该点与 ,把该点与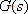 的所有零、极点连接成向量,并将这些向量分别以极坐标的形式表示: 的所有零、极点连接成向量,并将这些向量分别以极坐标的形式表示: 
则式(5-3)可改写为 由上式得到其对应的幅值和相角: 同理,可求得对应于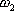 的 的 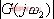 和 和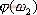 。如此继续下去,就能得到一系列幅值和相位与频率 。如此继续下去,就能得到一系列幅值和相位与频率 的关系,其中幅值随频率变化而变化的特性称为系统的幅频特性,相角随频率变化而变化的特性称为系统的相频特性。 的关系,其中幅值随频率变化而变化的特性称为系统的幅频特性,相角随频率变化而变化的特性称为系统的相频特性。
例5-1绘制系统的幅频和相频特性曲线... 设一线性系统的传递函数为 解:传递函数零、极点的分布如图5令  ,代入式(5即当 ,代入式(5即当  时,频率特性的幅值 时,频率特性的幅值 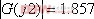 ,相角 ,相角 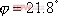 。代入不同的频率 。代入不同的频率  值,重复上述的计算,就可求得对应的一组 值,重复上述的计算,就可求得对应的一组 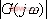 和 和 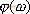 值。据此,也可由下面的Matlab 值。据此,也可由下面的Matlab figure(1),plot(w,x(:)),axis([0,10,0,3]),xlabel('频率(弧度)'),ylabel('幅值');> figure(2),plot(w,y(:)),axis([0,10,-120,40]),xlabel('频率(弧度)'),ylabel('相角')> 5.1.2 由实验方法求频率特性 系统的频率特性也可用实验方法得到。图5-3给出了一种求取系统频率特性的实验接线方法,它由一台正弦信号发生器、系统或元件装置和双踪示波器组成。信号发生器的频率范围由被测试的实验装置决定,双踪示波器的一路用于测量输出、输入信号的比值,即系统的幅频特性: 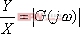 ,另一路用于测量输出信号与输入信号的相位差,即系统的相频特性: ,另一路用于测量输出信号与输入信号的相位差,即系统的相频特性: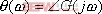 。通过不断改变输入信号的频率 。通过不断改变输入信号的频率 值,应可以得到系统的频率特性。 值,应可以得到系统的频率特性。 5.1.3 频率特性的基本概念 5.1.3 频率特性的基本概念
线性定常系统的频率特性和时域响应是一致的。在频率特性已知的情况下,可通过数值或解析的方法得到系统的时间响应。 如果一个系统的频率特性已知,则可根据反富里叶级数示取系统的时间响应。令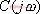 为控制系统输出的频率特性,则由> 为控制系统输出的频率特性,则由> >可得到系统输出的时间响应。上面的积分式可通过解析法或根据频特性图由数值法求得。 反过来,若已知系统的时间响应,也可求出系统的频率特性。为了方便理解,下面先以R-C电路为例,并说明频率特性的物理意义。 R-C电路的传递函数为 >设输入电压 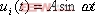 ,由复数阻抗的概念求得 ,由复数阻抗的概念求得 

技术专区
|
|
评论