4.6.1 参数根轨迹 ⒈引言 前面讨论系统根轨迹的绘制方法时,都是以开环增益K为可变参数,这是在实际上最常见的情况。上述以开环增益K 为可变参量绘制的根轨迹称为常规根轨迹。从理论上讲,可变参量可以选择为系统的任何参数,如开环零、极点,时间常数和反馈系数等,这种以K以外的系统其他参量作为可变参量绘制的根轨迹,称作参数根轨迹,又称广义根轨迹。用参数根轨迹可以分析系统中的各种参数,如开环零、极点,时间常数和反馈系数等对于系统性能的影响。
⒉思路和方法
如果选择系统其他参量为可变参量时,引入等效传递函数的概念,即作一个变换,使得此可变参量在等效传递函数中相当于开环增益K的位置,则上面介绍的幅角、幅值条件和绘制根轨迹的各种规则都依然有效。
上述变换的方法是对系统的特征方程作一个除法,即以特征方程中不含有该参数项的各项去除该方程,便可得到 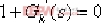 的形式,其中 的形式,其中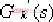 ,就是要引入的等效传递函数。 ,就是要引入的等效传递函数。
例4-4 设反馈系统如图4-16所示 ,试绘制以a为参变量的根轨迹。 ⑴. 常规方法 ⑴. 系统的开环传递函数为 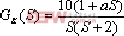 系统的特征方程为 
以不含a的项,即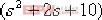 ,除以上式得 ,除以上式得 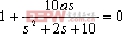
得等效开环传递函数: 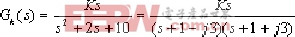
式中 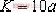 据此,可用“常规方法”作出其根迹,如图4-17所示(可证明,其部分根迹为园弧)。 ①.根迹的起迄点及条数:
两条根迹分支,分别起始于开环极点-1+j3、-1-j3,终止于开环零点0和s平面∞处。 ②.实轴上的根迹:
负半实轴为根迹。 ③.会合点: 由 。 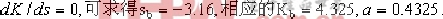
④.复数极点-1+j3出射角:
⑵.“MATLAB”方法 ①解本题的MATLAB程序exe44.m % ks/(s2+2s+10)
n=[1 0]
d=[1 2 10]
rlocus(n,d) ②执行本程序,可得图4-17参数根轨迹图。
4.6.2 多回路系统的根轨迹
1.引言 前面介绍单环系统根迹,不仅适合单环,而且也适合多环系统。
2.思路和方法
先作内环根迹,再用幅值条件试探求出内环的闭环极点,进而作为外环的一部分开环极点,再画出外环的根迹。 例4-5 设一双环反馈系统,如图4-18所示 。试绘制以 c为参变量的根轨迹。 ⑴.常规方法 ①.先作内环根迹:
内环开环传递函数为: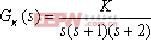 此与例4-1相同,这里不再重复。 ②.求出 =1.06 时的内环闭环极点(用试探法):
由§4―3可知,为:-0.33+j0.58、 -0.33-j0.58、 -2.33 ③.内环的闭环传递函数为: 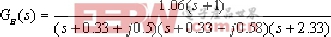
④. 内环化简后外环的开环的传递函数为:
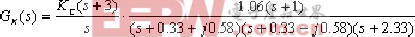
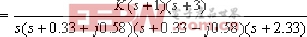
⑤.外环(系统)根轨迹: ·根轨迹有四条分支: 分别自0, -2.33,-033+j0.58,0.33-j0.58。至-1,-3,和s平面∞处。 ·实轴上根迹: 在 0 至-1,-2至-2.33,-3至-∞是根轨迹。 ·根迹渐近线: 由公式求得σα=0.5,α=±90B 。 ·复数极点-0.33+j0.58,外的出射角: φ=8.06B 。 ·根迹与虚轴交点: 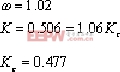
·系统外环根迹: 如图4-19所示. ⑵.“MATLAB”方法 ①.解本题的MATLAB程序exe45.m:
% k(s+1)(s+3)/s(s+0.33+0.58i)(s+0.33-0.58i)(s+2.33)
z=[-1 –3]’;
p=[0 –2.33 –0.33+0.58i –0.33-0.58i]’;
k=1;
[n,d]=zp2tf(z,p,k);
rlocus(n,d)
title(‘4-19’) ②.执行本程序,可得外环根轨迹图4-19。 |
评论