低压差线性稳压器（LDO）的噪音问题解析（二）

　　放大参考噪声

　　TI TPS74401 LDO 用于测试和测量。表 1 列出了常见配置参数。请注意，为了便于阅读，TPS74401 产品说明书的软启动电容器 CSS 是指降噪电容器 CNR。

　　表 1 设置参数

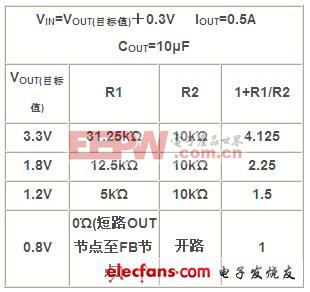
　　首先，使用一个可忽略不计的小 CNR，研究放大器增益的影响。图 6 显示了 RMS 噪声与输出电压设置的对比情况。如前所述，主要噪声源 VN（REF） 通过反馈电阻器 R1 和 R2 的比放大。我们将方程式 7 修改为方程式 8 的形式：

　　其中，VN（Other）为所有其它噪声源的和。

　　如果方程式 8 拟合y=ax + b的线性曲线，如图 6 中红色虚线所示，则 VN（REF）（斜率项）可估算为 19 µVRMS，而 VN（Other）（y 截距项）为 10.5 µVRMS。正如在后面我们根据“降噪（NR）引脚效应”说明的那样，CNR 的值为 1pF，目的是将 RC 滤波器效应最小化至可忽略不计水平，而 GRC 被看作等于 1。在这种情况下，基本假定 VN（REF） 为主要噪声源。

　　请注意，当　OUT　节点短路至 FB 节点时噪声最小，其让方程式 8 的放大器增益（1 + R1/R2）等于1（R1=0）。图 6 显示，该最小噪声点约为 30 µVRMS。

　　抵销放大参考噪声

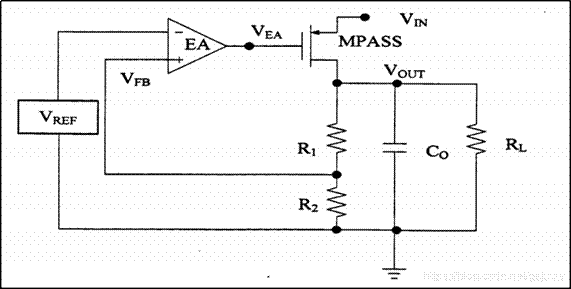
　　本小节介绍一种实现最小输出噪声配置的有效方法。如图 7 所示，一个前馈电容器 CFF 向前传送（绕开）R1 周围的输出噪声。这种绕开或者短路做法，可防止在高于 R1 和 CFF 谐振频率 fResonant 时参考噪声因误差放大器增益而增加，其中：

　　输出噪声变为：

　　图 7 使用噪声最小化前馈电容（CFF） 的 LDO 拓扑

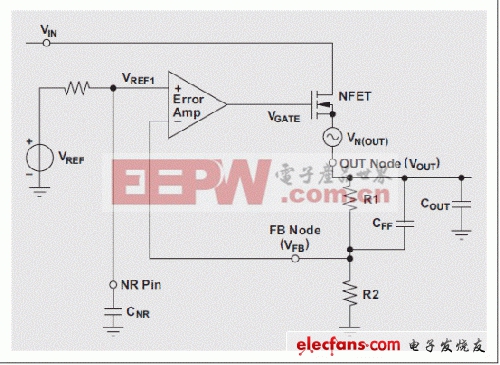
　　图 8 显示了RMS噪声相对于前馈电容 （CFF） 和不同输出电压设置的变化。请注意，每个 RMS 图线上各点代表上述电路状态下整个给定带宽的完整噪声统计平均数。正如我们预计的那样，所有曲线朝 30 µVRMS 左右的最小输出噪声汇集；换句话说，由于 CFF 效应，噪声汇聚于 VN（REF） + VN（Other）。

　　图 8 前馈电容对噪声的影响

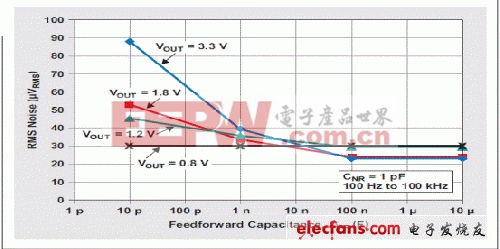
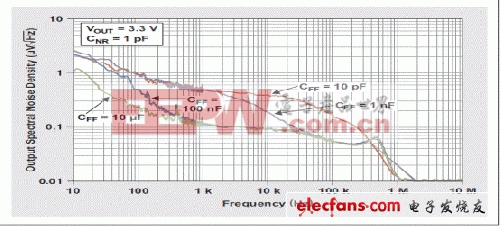
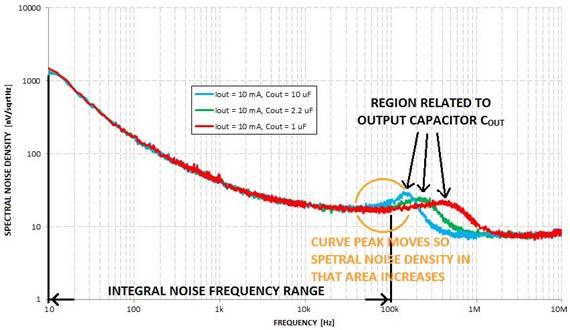
　　图 8 对此进行了描述。CFF 值大于 100nF时，方程式 8 中1 + R1/R2 的放大器增益被抵销掉。出现这种情况的原因是，尽管低频噪声未被 CFF 完全抵销，但是低频噪声对 RMS 计算的总统计平均数影响不大。为了观察 CFF 的实际效果，我们必需查看噪声电压的实际频谱密度图（图9）。图9表明，CFF=10µF 曲线的噪声最小，但是某些频率以上时所有曲线均接近于这条最小噪声曲线。这些频率相当于由 R1 和 CFF 值决定的谐振极点频率。R1 等于 31.6 k? 时计算得到的 CFF值，请参见表 2。

　　表 2 计算得谐振频率

　　图 9 表明，50 Hz 附近时，CFF=100 nF 曲线转降。5 kHz 附近时，CFF=1 nF 曲线转降，但是 CFF=10 pF 时谐振频率受 LDO 噪声总内部效应影响。通过观察图 9，我们后面均假设 CFF=10µF 最小噪声。

　　图 9 各种 CFF 值的输出频谱噪声密度

　　降噪 （NR） 引脚的效果

　　在 NR 引脚和接地之间使用 RC 滤波器电容（CNR）时，GRC 下降。图 10 表明 RMS 噪声为 CNR 的函数（参见图 5）。稍后，我们将在第三段“其它技术考虑因素”中说明这两条曲线的差异。

　　图 10 RMS 噪声与降噪电容的关系

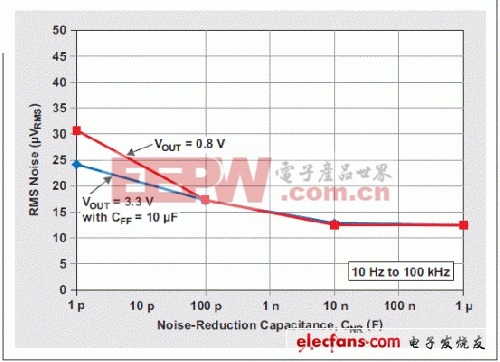
　　图 10 利用 10 Hz 到 100 kHz 更宽融合范围，来捕捉低频区域的性能差异。CNR=1pF 时，两条曲线表现出非常高的RMS噪声值。尽管图 10 没有显示，但不管是否 CNR=1pF，都没有 RMS 噪声差异。这就是为什么在前面小节“放大参考噪声”中，我们把GRC被看作等于 1 的原因。

　　正如我们预计的那样，随着 CNR 增加，RMS 噪声下降，并在 CNR=1µF 时朝约12.5 µVRMS 的最小输出噪声汇聚。

　　CFF= 10 µF 时，放大器增益（1 + R1/R2）可以忽略不计。因此，方程式 8 可以简写为：

　　正如我们看到的那样，VN（Other） 并不受 CNR 影响。因此，CNR 保持 10.5 µVRMS，其由图 6 所示数据曲线拟合度决定。方程式 10 可以表示为：

　　接下来，我们要确定 GRC 降噪电容的影响，这一点很重要。图 10 中曲线的最小测量噪声，让我们可以将方程式10改写为：

　　其中，求解VN（REF） × GRC 得到 2 µVRMS。增加 CNR 会使参考噪声从19.5 µVRMS降至 2 µVRMS，也就是说，在 10 Hz 到 100 kHz 频率范围，GRC 从整数降至 0.1 （2/19.5） 平均数。

　　图 11 显示了 CNR 如何降低频域中的噪声。与图 9 所示小 CFF 值一样，更小的 CNR 开始在高频起作用。请注意，CNR 最大值 1µF 表明最低噪声。尽管 CNR = 10 Nf 曲线表明最小噪声几乎接近于 CNR = 1 µF 的曲线，10-Nf 曲线显示30Hz 和100Hz 之间有一小块突出部分。

　　图 11 不同 CNR 值时输出频谱噪声密度与频率的关系

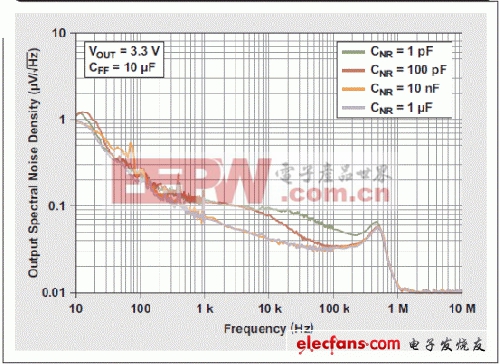
　　图8所示曲线（CNR = 1 pF），可改进为图 12（CNR = 1 µF）。图 8 显示 CFF = 100 Nf 和 CFF = 10 µF 之间几乎没有 RMS 噪声差异，但是图 12 清楚地显示出了差异。

　　图 12 中，不管输出电压是多少，CFF = 10 µF 和 CNR = 1 µF 均带来最低噪声值12.5 µVRMS，也即最小 GRC 值（换句话说，RC滤波器的最大效果）为 0.1。12.5 µVRMS 值为 TI 器件 TPS74401 的底限噪声。

　　图 12 噪声优化以后 RMS 噪声与前馈电容的关系

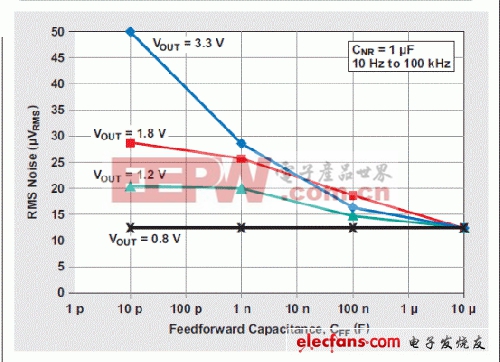
　　当我们把一个新LDO器件用于噪声敏感型应用时，利用大容量CFF和CNR电容确定这种器件的独有本底噪声是一种好方法。图12表明RMS噪声曲线汇聚于本底噪声值。
其他技术考虑因素

　　降噪电容器的慢启动效应

　　除降噪以外，RC滤波器还会起到一个RC延迟电路的作用。因此，较大的CNR值会引起稳压器参考电压的较大延迟。

　　前馈电容器的慢启动效应

　　CFF利用一种机制绕过R1反馈电阻AC信号，而凭借这种机制，其在激活事件发生后VOUT不断上升时，也绕过输出电压反馈信息。直到CFF完全充电，误差放大器才利用更大的负反馈信号，从而导致慢启动。

　　为什么高VOUT值会导致更小的RMS噪声

　　在图8和图10中，相比VOUT=0.8V的情况，VOUT=3.3V曲线的噪声更小。我们知道，更高的电压设置会增加参考噪声，因此这看起来很奇怪。对于这种现象的解释是，由于CFF连接至OUT节点，因此除绕过电阻器R1的噪声信号以外，CFF还有增加输出电容值的效果。图12表明，由于参考噪声被最小化，我们便可以观测到这种现象。

　　RMS噪声值

　　由于TPS74401的本底噪声为12.5 µVRMS，它是市场上噪声最低的LDO之一。在设计一个超低噪声稳压器过程中，12.5 µVRMS绝对值是一个较好的参考值。

　　结论

　　本文深入探讨了LDO器件的基本噪声以及如何将其降至最小，具体包括：

　　每种电路模块对输出噪声的影