基于凌华PCI-9846高速数字化仪的复杂超声场自动检测与分析（三）

5.系统功能的验证

　　为了验证系统的主要功能，选择一标准的凹球壳自聚焦超声换能器，连续波超声功率源驱动进行超声场声压分布参数的验证测试。换能器设计的几何参数分别为：换能器辐射面出口半径r=30mm，球壳曲率半径R=90mm，辐射中心频率f=1.3MHz，水介质的声速取1500m/s。测量声场的关键参数包括声压，声强和声焦域等，相应描述声场的基本形式主要有轴线声压曲线图，焦平面径向声压曲线图，焦平面声场曲面图，焦斑三维立体图。

　　经过测试换能器轴线声压曲线图显示了轴线上声压幅值随距离的变化的规律。水听器初始位置为声束中心轴线距离换能器40mm，经逐点扫描到140mm处结束，各点间距为0.5mm，测量值与理论值验证的结果如图5-1所示：

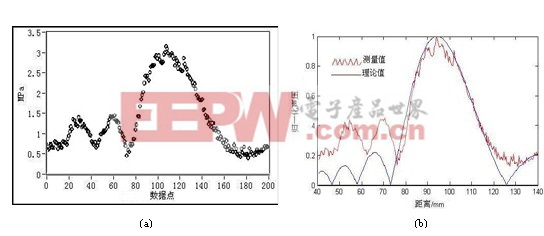
　　图5-1 轴向声压分布的理论值与测量值；（a）本文系统的实际测量值 （b）聚焦超声场理论模型仿真值和测量值比较

　　图5-1（a）是本文开发的系统的实际测量的数据值，该数据点是由机器人单轴扫描方式测试而得。图5-1（b）是在轴向上根据经典声场轴向声压分布模型建模计算的声压理论值与实测值比较的结果，波动的曲线是实际测量值，光滑实线是理论模型值。由模型可知在焦点以外的声压分布显示为低能量振荡，并逐渐衰减，而且在近场区和远场区的衰减幅度并不对称。测试结果显示测量值与理论值在主峰处拟和得很好，但是在旁瓣处，测量的声压值偏大，主要由于高频超声换能器在连续脉冲的激励下产生复杂的谐波，水听器和凌华科技9846H数字化仪响应频率范围宽，检测到的多种谐波频率分量叠加产生的能量，而理论模型和手工示波器检测固定在一个核心频率处，使信息不全。

　　由于发射换能器为凹球壳面，传播的波面也为球面，可以测量在焦平面一条直径的声压曲线图，作为超声场分布的一个特性，反映了沿径向声压幅值随距离的变化规律，扫描各点间距为0.05mm，实验结果如图5-2所示。

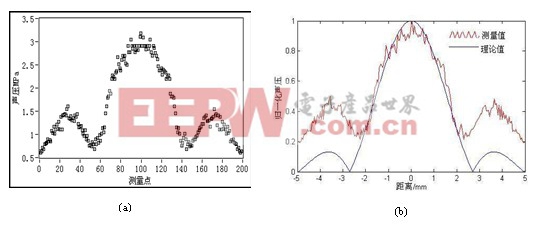
　　图5-2 焦平面面径向声压分布的理论值与测量值比较结果；（a）测量系统的实际测量值 （b）聚焦超声场理论模型仿真值和测量值比较结果

　　图5-2（a）是本文系统的实际测量的数据点，该数据是由单轴扫描方式测得。图5-2（b）是在焦平面径向上经经典声压理论建模计算的值与实际值比较结果。波动的曲线是实际测量值，光滑实线是理论模拟值，可见焦平面声压分布是振荡而且沿中心点对称分布的。从图5-2（b）理论值与实际测量值比较结果可知，主峰处拟和得比较好，但是在旁瓣处，实际测的值丰富，原因仍是由于超声换能器有复杂的谐波，水听器与凌华科技9846H数字化仪频率响应宽，可采集到谐波能量，理论模型只是核心频率建立的模型。

　　在焦平面上，按规定的扫描路径，顺序测量声场中各点的声压值，扫描步距为0.5mm，实验结果和焦平面的理论模型如下图5-3所示：

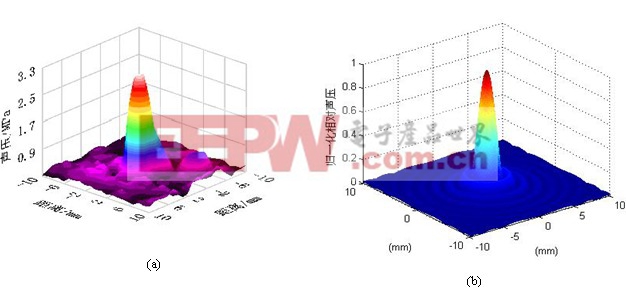
　　图5-3 测试换能器焦平面声压分布的实际测量值（a）与声场理论模型仿真值

　　图5-3图中（a）图是基于精密机器人测量和分析系统的实际测量的焦平面数据点，该数据点是由机器人声场扫描运动软件测试并保存，经测量超声声场分析软件处理而得。（b）图是由在焦平面上建模计算的声压理论值。从焦域的二维模型可知，焦平面上声压的能量比较集中，声压沿径向是振荡衰减的，非焦点区域的能量分布很低，而且单频凹球壳的声场在焦平面是沿超声换能器的主轴线中心对称分布的。比较实际值与理论值可知，在聚焦区域的主峰处拟合很好，在非聚焦区域