如何利用ADUCM360精密监控热电偶温度(二)
用于测试本电路的源代码可从ADuCM360产品页面下载(zip压缩文件)。
UART配置为波特率9600、8数据位、无极性、无流量控制。如果本电路直接与PC相连,则可以使用“超级终端” (HyperTerminal)等通信端口查看程序来查看该程序发送给UART的结果,如图3所示。
图3.“超级终端”通信端口查看程序的输出
测量热电偶和RTD的温度,以获得温度读数。通过查找表,将RTD温度转换为它的等效热电偶电压(可查看ISE公司的ITS-90 T型热电偶表)。这两个电压相加以得出热电偶的 绝对温度值。
首先,V1是热电偶两条线之间测得的电压。通过查找表,测量RTD电压并转换为温度值;然后,该温度值再转换为它的等效热电偶电压(V2)。随后,V1和V2相加得出总热电 偶电压值,此数值经转换后作为最终的温度测量值。
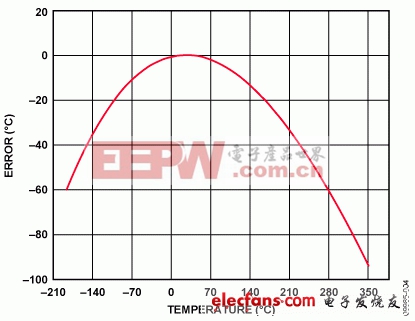
图4. 使用简单线性逼近法时的误差
最初,这一转换是基于一个简单的线性假设:热电偶的温度为40V/°C。从图4可以看出,只有针对0°C左右的小范围温度,如此转换所产生的误差才是可以接受的。计算热电偶温度的更好方法是对正温度使用6阶多项式,对负温度使用7阶多项式。这需要进行数学运算,导致计算时间和码字大小增加。适当的折衷是针对固定数量的电压计算相应的温度,然后将这些温度存储在一个数组中,其间的值利用相邻点的线性插值法计算。从图5可以看出,使用这种方法时误差显著降低。图5表示使用理想热电偶电压的算法误差。
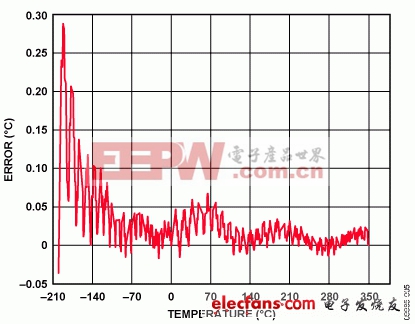
图5. 使用分段线性逼近法时的误差
图6表示在ADuCM360上采用ADC1测量全热电偶工作范围内的52个热电偶电压,所产生的误差。整体最大的误差为《1°C。
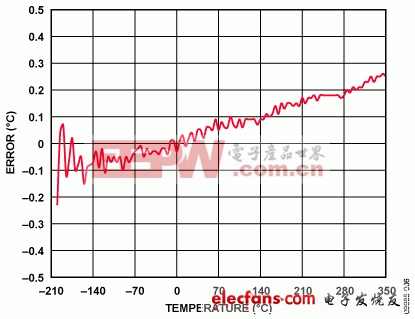
图6. 使用分段线性逼近法时的误差(采用ADuCM360/ADuCM361测量的52个校准点)
像热电偶一样,RTD温度可使用查找表的方法计算与实现。注意,描述RTD温度与电阻关系的多项式与描述热电偶的多项式不同。
常见变化
ADP1720 可以代替AD
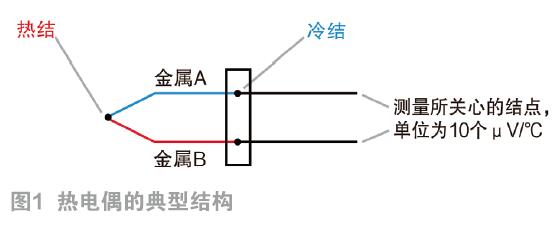
热电偶相关文章:热电偶原理



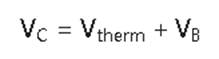



评论