掌握AI尚方宝剑:注意力机制
1 前言
经过上一期的范例和解说,您对于相似度的计算,已经建立良好的基础了。就可以轻易地来理解和掌握注意力(Attention) 机制。这项机制在许多大语言模型( 如ChatGPT、Gemma等) 里,都扮演了极为关键性的角色。再看看最近声势非常浩大的Sora,其关键技术——DiT(Diffusion Transformer) 的核心也是注意力机制。
于是,本文就从上一期介绍的相似度(Similarity) 基础,继续延伸到注意力机制。此外,更重要的是:此项机制也是可以学习的(Learnable),于是就来把它包装于NN模型里,成为可以训练的注意力模型(Attention model)。
典型的Attention 模型, 包括两种: 交叉注意力(CrossAttention) 和自注意力(SelfAttention)。本文就先来说明SelfAttention 模型的计算逻辑,及其训练方法。
2 以“企业经营”来做比喻
首先来做个比喻。例如,一个公司有三个部门,其投资额( 以X表示),经过一年的经营绩效比率( 以W表示),其营收额( 以V 表示),如图1所示。

图1
这三部门投资额是:X=[10, 6, 2.5],其单位是---百万元。经过一年的经营,其营收比率是:W=[2.0],就可以计算出营收金额是:V=[20, 12, 5]。
接下来,公司的经营团队开始规画下一年度的投资方案,针对未来新的商业投资获利注意点,拟定一个投资预算分配表( 即注意力表),然后计算出新年度的投资预算金额( 单位:百万元),如图2所示。
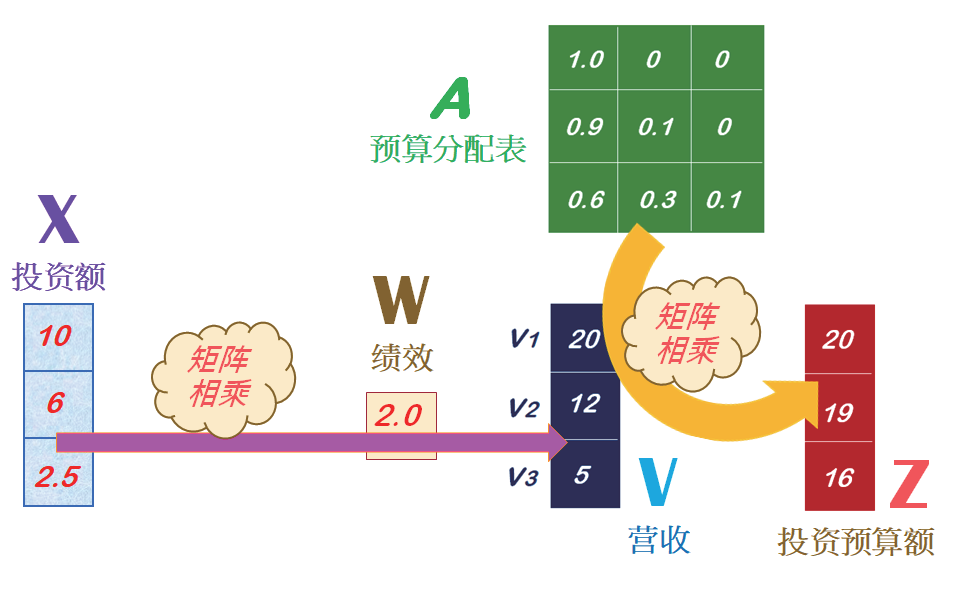
图2
其中的预算分配表,可以是相似度矩阵(Similarity matrix),亦即经由相似度的计算而来。现在,就来理解上图的计算逻辑,请观摩一个Python的实现代码:
# ax01.py
import numpy as np
import torch
X = torch.tensor([[10.0],[6.0],[2.5]]) # 投资额
W = torch.tensor([[2.0]]) # 经营绩效
V = X.matmul(W) # 计算营收
A = torch.tensor(
[[1.0, 0., 0.],
[0.9, 0.1, 0.],
[0.6, 0.3, 0.1]]) # 预算分配表
Z = A.matmul(V) # 计算分配额
print(‘n 投资预算额Z:’)
print(Z) #np.round(Z.detach().numpy()))
#END
接着,就执行这个程序。此时就输入X和W,计算出V值。然后输入相似度表A,计算出新年度的投资预算额,并输出如下:

3 使用Attention计算公式
在上一期里,已经说明了,相似度矩阵是直接计算向量的点积(Dot-product),即将两向量的对应元素相乘再相加。然后,这相似度矩阵再除以它们的欧氏长度的乘积,将相似度的值正规化,就得到余弦(Cosine)相似度。而且,如果将上述的相似度矩阵,在经由Softmax() 函数的运算,就得到注意力矩阵(Attention weights) 了。例如,有两个矩阵:Q 和K,就能计算出注意力矩阵,如图3 所示。
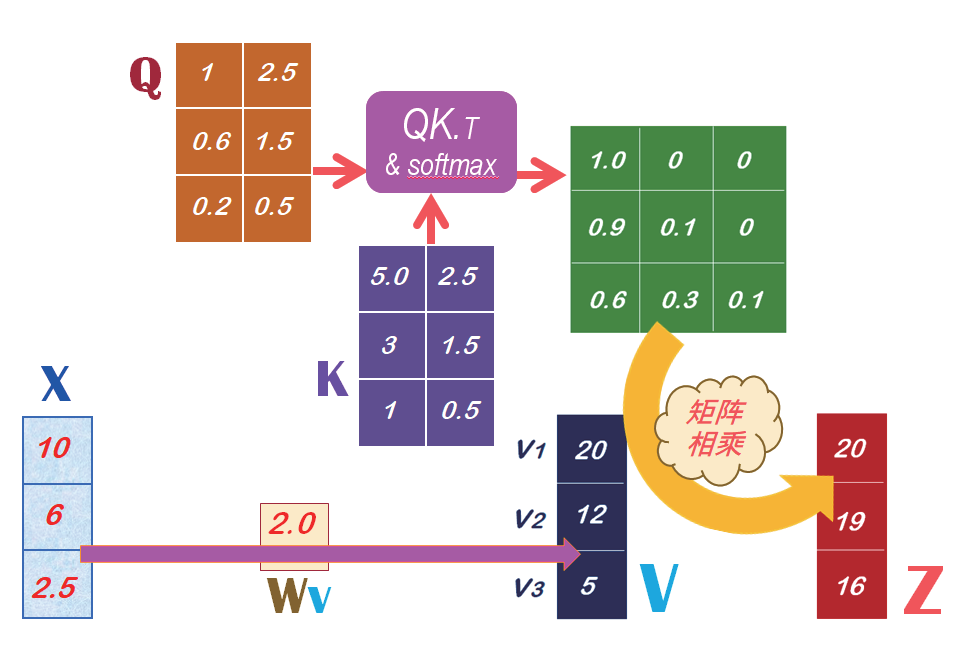
图3
那么,就可以继续思考一个重要问题,就是:如何计算出Q和K矩阵呢? 答案是:可以由SelfAttention模型来预测出来。也就是,由输入数据X来与SelfAttention模型的权重Wq相乘而得到Q。同时,也由输入数据X来与这模型的权重Wk 相乘而得到K,如图4所示。
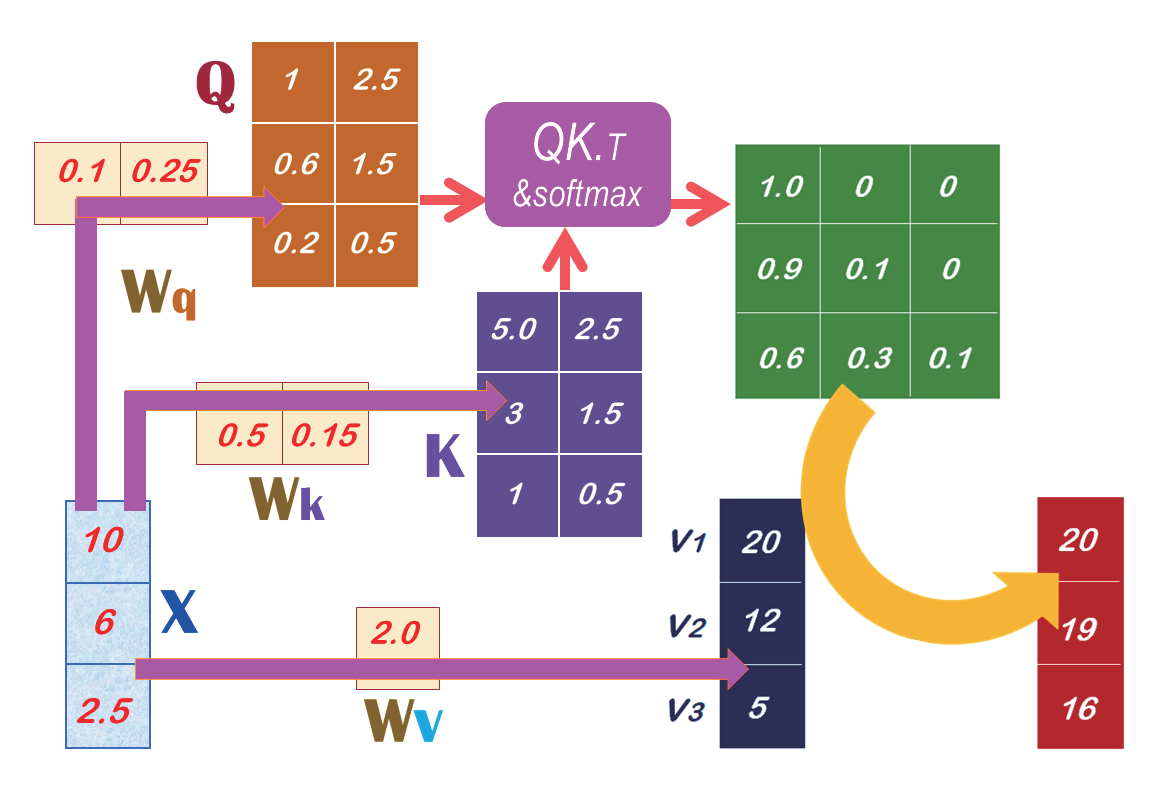
图4
当我们把上图里的Wq、Wk和Wv权重都放入SelfAttention模型里, 就能进行机器学习(Machine learning) 来找出最佳的权重值( 即Wq、Wk 和Wv),就能预测出Q、K 和V 了。并且可继续计算出A 了。
4 训练SelfAttention模型
现在就把Wq、Wk 和Wv 都放入SelfAttention 模型里。请观摩这个SelfAttention 模型的代码范例,如下:
# ax02.py
import numpy as np
import torch
import torch.nn as nn
import torch.nn.functional as F
class SelfAttention(nn.Module): # 定义模型
def __init__(self):
super(SelfAttention, self).__init__()
self.Wq = nn.Linear(1, 2, bias=False)
self.Wk = nn.Linear(1, 2, bias=False)
self.Wv = nn.Linear(1, 1, bias=False)
def forward(self, x):
Q = self.Wq(x)
K = self.Wk(x)
V = self.Wv(x)
Scores = Q.matmul(K.T)
A = F.softmax(Scores, dim=-1) # Attention_weights
Z = A.matmul(V) # 计算Z
return Z, A, V
model = SelfAttention() # 建立模型
criterion = nn.MSELoss()
optimizer = torch.optim.Adam(model.parameters(),lr=0.004)
# 输入X
X = torch.tensor([[10.0],[6.0],[2.5]])
# 设定Target Z
target_attn = torch.tensor([[20.0],[19.0],[16.0]])
print(‘展开训练1800 回合...’)
for epoch in range(1800+1):
Z, A, V = model(X) # 正向传播
loss = criterion(Z, target_attn) # 计算损失
optimizer.zero_grad() # 反向传播和优化
loss.backward()
optimizer.step()
if(epoch%600 == 0):
print(‘ep=’, epoch,‘loss=’, loss.item())
# 进行预测
Z, A, V = model(X)
print(‘n----- 预算分配表A -----’)
print(np.round(A.detach().numpy(), 1))
print(‘n----- 投资预算额Z -----’)
print(np.round(Z.detach().numpy()))
#END
然后就执行这个程序,此时会展开1800 回合的训练。在训练过程中,回持续修正模型里的权重( 即Wq、Wk和Wv),并且其损失(Loss) 值会持续下降,如下:

一旦训练完成了,就可以展开预测(Prediction)。此时,就计算出Q、K 和V,然后继续计算出A 和Z 值。
5 结束语
本期基于相似度计算,继续说明注意力机制的计算逻辑,建立SelfAttention模型,并且训练1800 回合,然后进行预测。
从这范例中,可以领会到SelfAttention模型能顺利捕捉到企业的经营规律,并进行准确的预测。
(本文来源于《EEPW》2024.4)




评论