AI神奇魅力的源点：相似度

1 前言

在本专栏去年的文章《从隐空间认识CLIP 多模态模型》里，已经介绍过了：CLIP 的核心设计概念是，把各文句和图像映射到隐空间里的一个点( 以向量表示)。其针对每一个文句和图像都会提取其特征，并映射到这个隐空间里的某一点。然后经由矩阵计算出向量夹角的余弦(Cosine) 值，来估计它们之间的相似度(Similarity)。

此外，在Transformer 里扮演核心角色的点积注意力(Dot-Product attention) 机制，其先透过点积运算，从Q与K矩阵计算出的其相似度(Similarity) 矩阵，然后继续计算出注意力(Attention) 矩阵。

于是本期就从简单的相似度出发，再延伸到注意力机制，并循序渐渐地扩大为典型的Transformer 模型。然后就能理解当今LLM 等大模型的魅力源头。例如，Sora 也采用注意力(Attention) 机制，以便于在影片生成过程中，能专注于文字提示的关注意图。这确保了相关细节被优先考虑，从而更准确、更忠实地表示人们所期待的场景。

2 简介余弦(Cosine)相似度

当人们看到事物( 如图像) 的特征时，很容易依据其特征来看出其相似性( 又称：相似度)，然后依据其特征的相似性，进行分门别类。例如有三张图像：

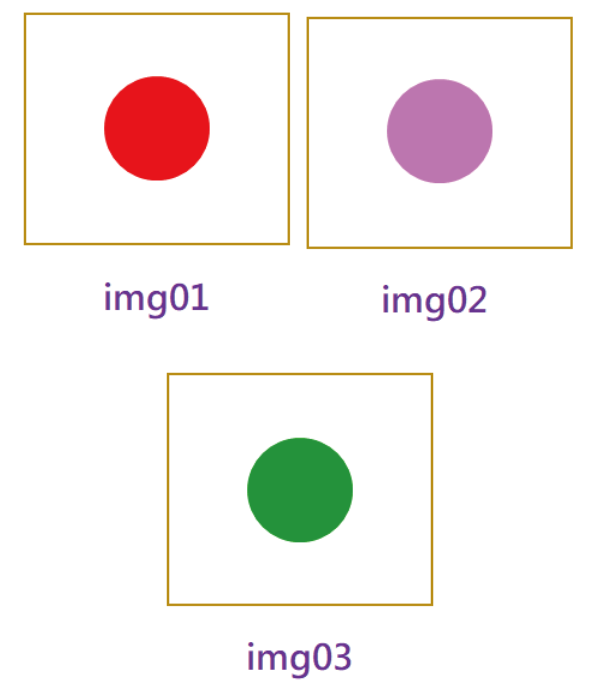
图1 三张简单图像

人们一眼就能分辨出来左边两张图(img01与img02) 的色彩比较相近( 相似)；而右边图与其他两者就比较不相似。AI也具有这样的能力，就是您已经熟悉的AI分类器( 模型) 了。由于AI 经常需要处理高维度的数据，例如常将图像、文句或文件表达为高维度欧式空间里的向量。此时，就常常使用余弦相似度(Cosine Similarity) 算法。可应用于侦测图像(Image) 之间的相似度( 又称：相似性)；也能应用于计算两个文句之间的相似度( 例如，同义词等)。

经由这算法，可以计算出事物( 表达为向量) 之间的相似程度，其值介于[-1, 1] 之间。数值愈高就表示两个向量愈相似。余弦相似度是基于两个向量的夹角来度量的。其计算两个向量之间夹角的余弦(Cosine) 值，来衡量它们之间的相似度。例如下图：

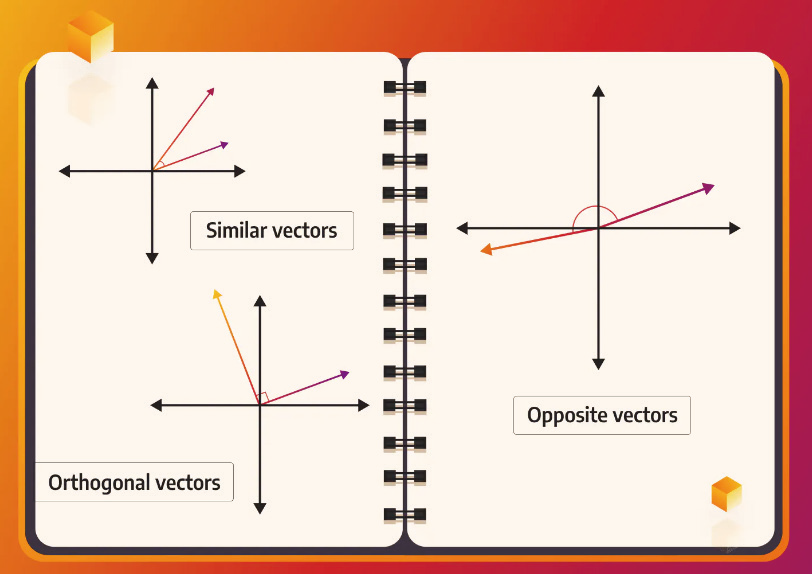
图2 Consine相似度

观察上图1-2里，其中的左上方的小图里，两个向量的夹角小于90 度，其余弦值大于0。而左下方的小图里，两个向量互相垂直，夹角是90 度，其余弦值等于0。至于右方的小图里两个向量的夹角大于90 度，其余弦值小于0。所以，余弦相似度的值是介于 -1与1之间。其值为-1，表示向量相反；其值为0，表示正交向量( 不相似)；而其值为1，表示相似向量。

上述图1-2 的范例是在二维空间里，计算二维向量的余弦相似度。此外，在AI( 机器学习) 里常将图像、文句或文件表达为高维度欧式空间里的向量。此时，也非常适合用余弦值来表达这些高维向量之间的相似度。

例如，从上图-1 里的各小图，取出其中心点( 像素)的RGB值，成为各小图的特征，就得到三维空间里的3个向量：

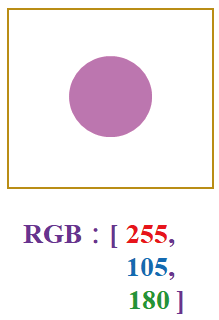
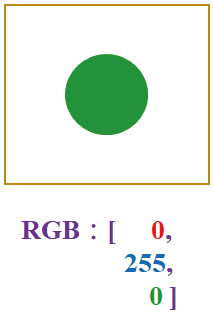
图3 萃取图像特征

RGB 值就成为各张图的特征了，也即是三维空间里的3个向量：

[ [255, 0, 0], [255, 105, 180], [0, 255, 0] ]

那么，如何表示上述3 个向量之间的余弦相似度呢?

3 认识相似度矩阵(Matrix)

首先来观摩一个Python 小程序，其代码如下：

# simi_01.py

import numpy as np

from sklearn.metrics.pairwise import cosine_similarity

# 定义三个3 维向量

x = np.array([[255,0,0],[255,105,180],[0,255,0]])

# 将向量归一化，这对于计算cosine similarity 很重要

normalized_x = x / np.linalg.norm(x, axis=1, keepdims=

True)

# 使用cosine_similarity 计算相似度

similarity_matrix = cosine_similarity(normalized_x)

print(“nCosine Similarity Matrix:”)

print(‘n’, similarity_matrix)

#END

接着，就执行这个程序。此时输入3 维向量：[[255,0, 0], [255, 105, 180], [0, 255, 0]]，然后计算出它们之间的余弦相似度，并输出相似度矩阵：

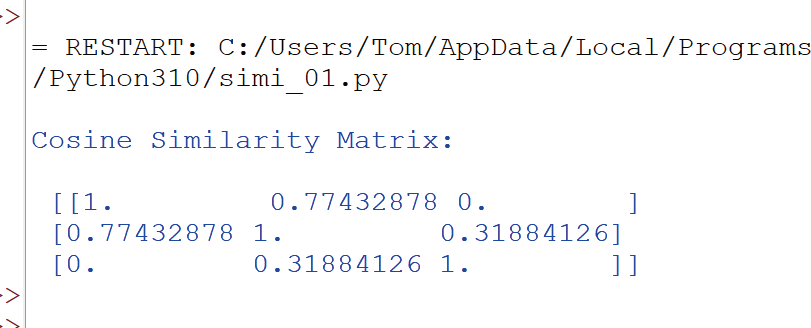
这个矩阵所表达的涵意是：

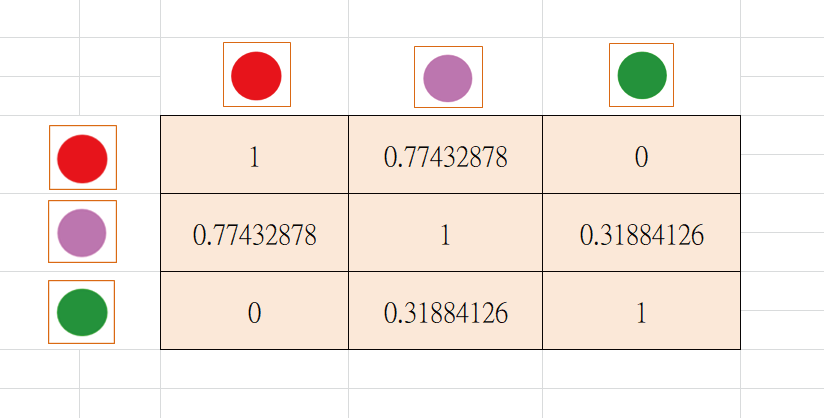
请看最上面一列(Row) 数值的意义是：针对左边图像(红色)而言，它与自己的相似度为1.0( 完全相似)；它与中间图像(粉红色) 的相似度约为0.77( 很相似)；而它与右边图像(绿色) 的相似度约为0.0( 不相似)。

再看第二列数值的意义是：针对中间图像(粉红色)而言，它与左边图像(红色) 的相似度约为0.77(很相似)；它与自己的相似度为1.0(完全相似)；而它与右边图像(绿色) 的相似度约为0.31(有一些相似)。

余弦相似度矩阵是直接计算向量的点积(Dotproduct)，即将两向量对应元素相乘再相加，再除以它们的欧氏长度的乘积，这样可以将相似度的值正规化，使之不受向量长度的影响，即不考虑向量长度，只考虑其夹角的余弦值。

4 延伸到注意力权重(Attention-weights)

刚才说明了，在计算余弦相似度时，我们先计算向量之间的点积，再进行正规化：除以它们的欧氏长度的乘积。

现在，我们将采取另一种途径：先计算向量之间的点积，再计算出注意力权重(Attention-weights)。现在，来观摩一个Python 小程序，其代码如下：

#simi_02.py

import torch

import torch.nn as nn

import torch.nn.functional as F

# 定义三个3 维向量

x = torch.tensor([

[255, 0, 0],

[255,105,180],

[0, 0, 255]], dtype=torch.fl oat32)

scores = x.matmul(x.T)

# 使用Attention-weights

attention_weights = F.softmax(scores, dim=1)

print(“nAttention-weights:”)

print(attention_weights)

#END

在注意力权重中，我们应用 Softmax() 函数，将点积相似度矩阵的每一行转换为概率分布，以表示每个向量对于其他向量的关注程度。这可以看作是一种注意力权重。

至于在余弦相似度中，不一定需要进行Softmax()转换，因为余弦相似度通常已经被正规化，它的范围在-1到1之间，所以不需要再转换为概率分布。于是，此程序执行时，就输出注意力权重矩阵，如下：

总之，注意力权重通常用于序列到序列模型的注意力机制，而余弦相似度，则更常用于评估向量之间的相似度而不涉及到注意力的权重分配。两者的选择取决于特定应用的需求。

5 结束语

本期说明了余弦相似度与注意力权重的概念，以及其计算方法。下一期将继续延伸到Self-Attention 机制、Cross-Attention机制和Transformer模型等。

（本文来源于《EEPW》2024.3）