MBD应用于霍尔组件位置选定
在直流无刷马达中,电磁仿真软件不仅可设计马达磁路本体,也可决定霍尔组件位置。本文采用Altair的电磁仿真软件Flux进行马达本体建模,在理论决定霍尔组件位置后提取磁通密度,再搭配系统开发平台软件建立六步方波电流驱动模型,完成符合物理定义的驱动与马达整体模型。
应用model-based design(MBD)来设计各种不同产品已是目前主流,尤其在马达设计时,电磁仿真软件的导入已是不可或缺的工具。然而在直流无刷马达此一产品中,电磁仿真软件不仅可设计马达磁路本体,也可决定霍尔组件(Hall Sensor)位置
直流无刷马达
直流无刷马达主要应用在风扇等开回路控制领域, 搭配霍尔组件(Hall Sensor)进行六步方波控制(图1)。霍尔组件为侦测马达转子角度进而决定六步方波开关次序。当磁通密度超越固定值时,霍尔组件讯号由0->1,降低在固定值下时讯号由1->0。故而霍尔组件的位置影响马达最终的扭力输出,接着使用Altair公司的电磁仿真软件Flux建立8极9槽马达,藉由理论决定霍尔组件位置提曲磁通密度后建立六步方波。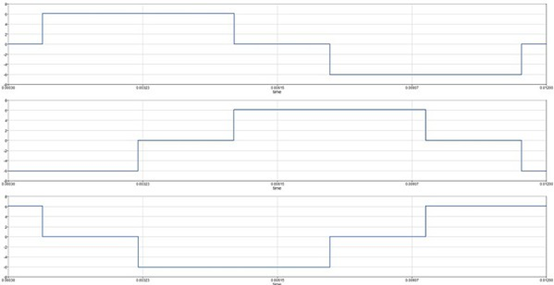
图1 : 六步方波控制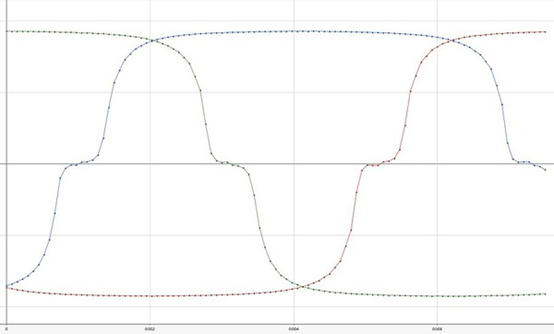
图2 : 磁通量梯型波
表1 转子角度与U相扭力关系
轉子角度 |
磁通量 |
電流 |
扭力 |
|
?? 0 |
0 |
0 |
0 |
|
30 |
1 |
1 |
1 |
|
90 |
1 |
1 |
1 |
|
150 |
1 |
1 |
1 |
|
180 |
0 |
0 |
0 |
表2 转子角度与UVW相扭力关系
轉子角度 |
U扭力 |
V扭力 |
W扭力 |
總扭力 |
|
0~30 |
0 |
1 |
1 |
2 |
|
30~90 |
1 |
0 |
1 |
2 |
|
90~150 |
1 |
1 |
0 |
2 |
|
150~180 |
0 |
1 |
1 |
2 |
马达扭力公式
马达扭力公式,如下方程序1所示。扭力由马达磁通量, 匝数与电流组成。匝数为纯量,磁通与电流为向量,霍尔组件位置决定电流向量角度,进而影响马达扭力输出。直流无刷马达的磁通波形为梯型波(设定峰值为1),如图2所示,电流为六步方波(同样峰值设定为1),磁通电流的夹角为90度,匝数同样为1下马达U相扭力如表1所示,将V相与W相扭力显示在表2,可见马达在不同转子角度时UVW各相对扭力的贡献,最终马达总扭力为定值。
Torque = N * ? * Irms * cosθ (1)
其中
N为马达匝数
?为马达磁通量
Irms为马达电流
θ为电流与磁通夹角
马达与电流建模
在Altair的电磁仿真软件Flux内建立 8极 9槽马达模型(图3),观察U相磁通量波形如图4所示的梯形波。输入马达的六步方波电流由Altair发行之系统开发平台软件Activate建立,由转子角度与转速计算得知六步方波的切换时序,确保电流与磁通量的夹角为90度,建立时间基准的六步方波电源,输入Flux的马达模块,扭力曲线如图5所示。
此模型的六步方波是由角度计算时间建立而成,并非实际的由霍尔组件切换状况形成,与实际状况仍有一段差距。因此接续将先采用理论计算UVW三相的霍尔组件位置,再于Flux内汇出这三个霍尔组件的磁通密度数值。将磁通密度数值汇入Activate软件,设定切换开关状态的数值后, 建立霍尔组件基准的六步方波并与时间基准的六步方波波形比较。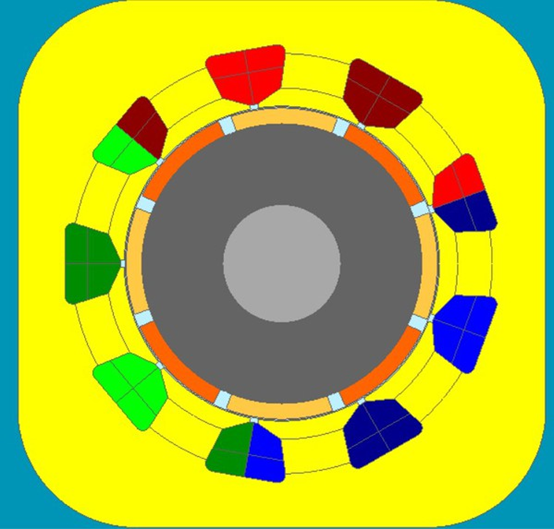
图3 : 8 极 9槽马达模型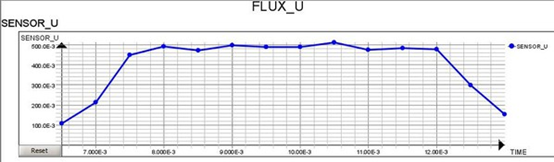
图4 : U相磁通波形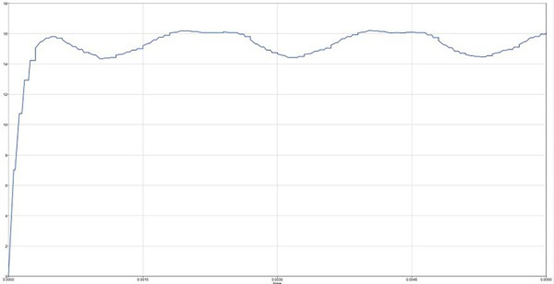
图5 : 时间基准六步方波产生的马达扭力曲线
霍尔组件位置
霍尔组件藉由侦测磁通密度的大小来决定状态为0或1,三个组件状态的改变建立如图1的六步方波,此即为电流的电气角度。电流与磁通量的夹角影响马达扭力。所以霍尔组件的位置要从磁通量角度开始考虑,也就是马达的定子齿部与转子磁石位置。
要决定霍尔组件位置,需先决定代表的定子齿部与磁石,不同的槽极数状况不同。范例马达 为3相8极9槽设计,单一相位分配到3个定子,取正中央定子齿部为代表来计算磁通量与电流的角度。槽距(机械角)为40度。马达极数为8极,极距(机械角)为45度,以U相来展开讨论。
如图3所示,可知 U相中央定子齿部的机械角为80度,正对深橘色的S磁石,此时的转子角度为U相的d轴状况。右 侧NS的磁中性点机械角为57.5度。磁中性点到中央定子齿部角度为80-57.5=22.5度,电气角度为22.5*4=90度。
方波为磁通量电气角为30度时,讯号由0→1如图6所示(以反电动势代替磁通),换算回机械角的话,NS磁中性点要转动30/4=7.5度,霍尔组件讯号由0→1,磁中性点原始角度为57.5度,转7.5度后角度为57.5+7.5=65度,此即为理论上U相霍尔组件位置,状态由0→1。
考虑绕线状况得 知V相霍尔组件位置为U相加上机械角120度即为65+120=185,同理W相组件为V相位置加上120 度,185+120=305度。将此三个霍尔组件位置标示如图7的X处所示。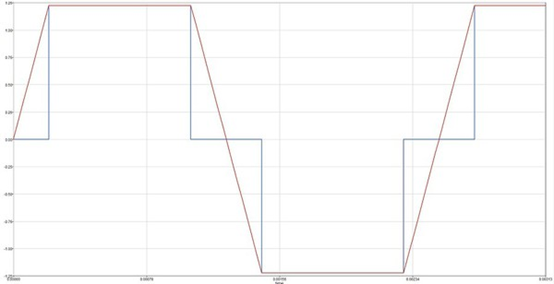
图6 : 电流与反电动势波形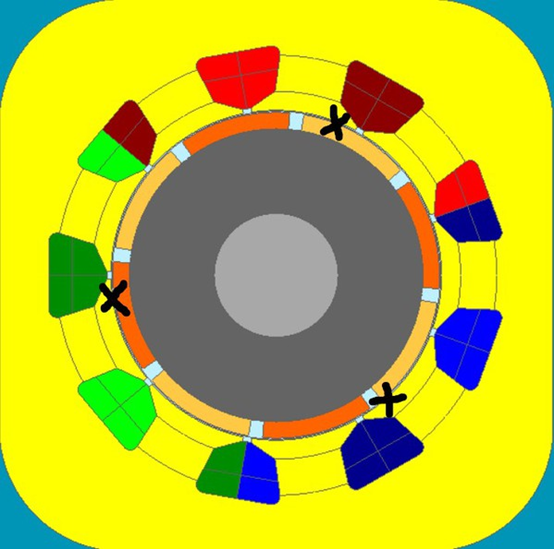
图7 : 霍尔组件位置
霍尔讯号建立六步方波
将三个霍尔组件位置处的磁通密度数值从 Flux内汇出后,再于Activate内汇入(图8),经过讯号处理设定切换0与1状态的数值后,即是霍尔组件的状态表(表3),进而完成建立六步方波模块。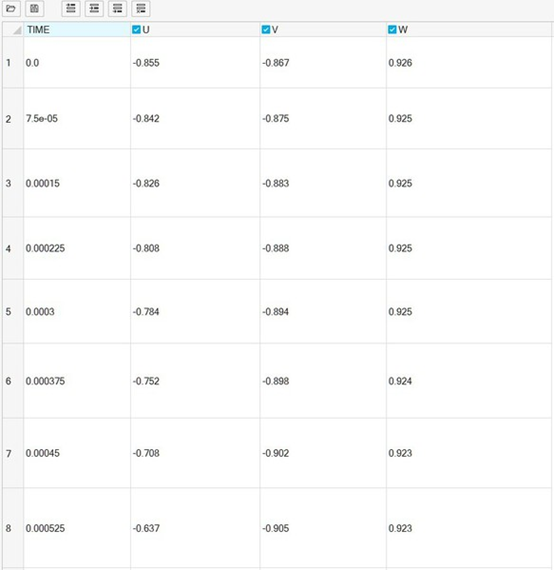
图8 : 霍尔组件讯号汇入
接下来,比较时间基准的方波与霍尔组件基准的方波波形(图9),可见两种方式建立的六步方波非常相似,霍尔组件基准建立的六步方波与实际状况相似,同时也吻合物理理论计算的结果。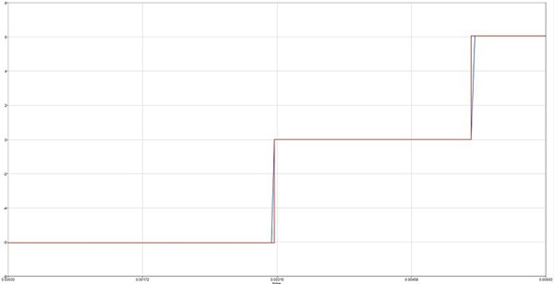
图9 : 两种六步方波波形比较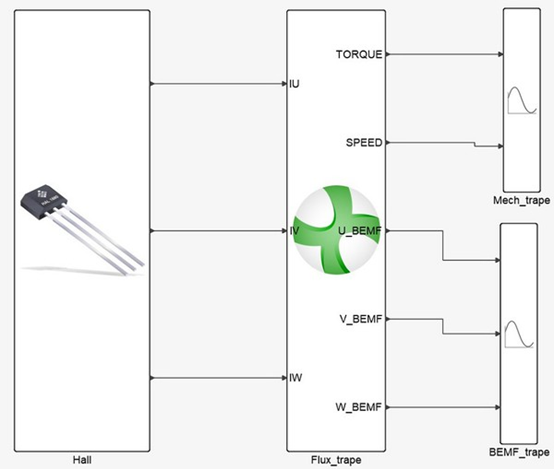
图10 : 霍尔组件控制马达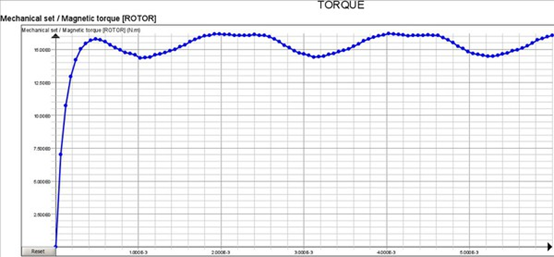
图11 : 马达扭力曲线
|
磁中性點角度 |
Hall ??U |
Hall ??V |
Hall ??W |
電氣角角度差 |
|
65~80 |
1 |
0 |
1 |
60 |
|
80~95 |
1 |
0 |
0 |
60 |
|
95~110 |
1 |
1 |
0 |
60 |
|
110~125 |
0 |
1 |
0 |
60 |
|
125~140 |
0 |
1 |
1 |
60 |
|
140~155 |
0 |
0 |
1 |
60 |
霍尔组件控制马达
确认霍尔组件基准的方波与时间基准的方波相同后,由霍尔基准的方波电流取代原本时间基准的方波电流,输入Flux当电流驱动,如图10所示。在马达为固定转速转动状态之下,整个运作顺序如下:
马达转子转动改变霍尔组件位置磁通密度;
磁通密度变化改变霍尔组件状态(0或1);
综合三个霍尔组件状态建立六步方波;
六步方波电流输入马达产生扭力。
整体模型,运作顺序皆与实际系统相同。
此模型仿真的马达扭力曲线如图11所示,与时间基准的结果(图5)相同,再次验正霍尔模型的正确性;同时吻合理论的马达总扭力为定值的结果。
结论
本文大费周章的从理论出发找出霍尔组件的位置,并以此建立霍尔组件基准的六步方波模型,其目的在于缩小模型与实物的差距,建立有物理理论根据的模型。此方法的好处是当处于开发阶段试作品发生问题时,可藉此模型来一步步找出问题的根源,确认是霍尔组件损坏,或位置放置错误,还是讯号处理有问题?可将假设的原因建立在模型内,观察仿真结果是否会产生跟实测时相同的问题?日积月累下,企业可累积研发单位的软实力与设计经验,不致受到人员变动造成能力流失的影响。
由于霍尔组件位置信息在初步设计时间即可获得,试作品设计时就可采用确定的组件固定方式 ,不需采用可变动的固定方式,试作测试确认位置后再改变成确定固定方式,加速产品开发速度与节省开发费用。更进一步采用此MBD方式,设计初期就可以规范制程中需要控制的变异处,如反电动势与霍尔讯号的角度,线圈绕线,以及转向与霍尔位置三者之间的关系,都可藉由MBD的信息建立项目文件。
藉由使用Flux与Activate软件,本文初步实现机与电讯号互传的方式,Flux产生磁通密度汇入Activate,Activate藉由磁通密度建立六步方波再输入Flux马达产生扭力,日后更可完善驱动模型,逐渐达到机电合一双向仿真的目标。
然而霍尔组件的位置会因不同马达槽极数的设计而有所变化,模拟工具需搭配专业理论知识才能发挥出MBD的好处,逐步达到数字双生(Digi Twins)的目标。
(本文作者陈志豪为佑谦科技电机顾问)




评论