有源带通滤波器的常见类型及应用电路

带通滤波器与任何其它滤波器一样，可以围绕晶体管和运算放大器等有源元件进行设计。带通滤波器是一种仅允许特定频带通过的电路，这个通带主要在截止频率之间，它们是fL和fH， 其中fL是较低的截止频率，fH是较高的截止频率。

带通滤波器与任何其它滤波器一样，可以围绕晶体管和运算放大器等有源元件进行设计。带通滤波器是一种仅允许特定频带通过的电路，这个通带主要在截止频率之间，它们是fL和fH， 其中fL是较低的截止频率，fH是较高的截止频率。

此外，中心频率用“fC ”表示，也称为共振频率或峰值频率。

f值必须始终小于fH的值。滤波器的通带不过是带宽。滤波器的增益在谐振或中心频率处最大，这称为总通带增益，使用“A max ”表示。

对于低通滤波器，此通带从0Hz开始，一直持续到从最大通带增益下降到-3dB处的谐振频率值。在高通滤波器的情况下，该通带从-3dB谐振频率开始，并在有源滤波器的最大环路增益值处结束。低通和高通响应的组合为我们提供了带通响应，具体如下图所示：

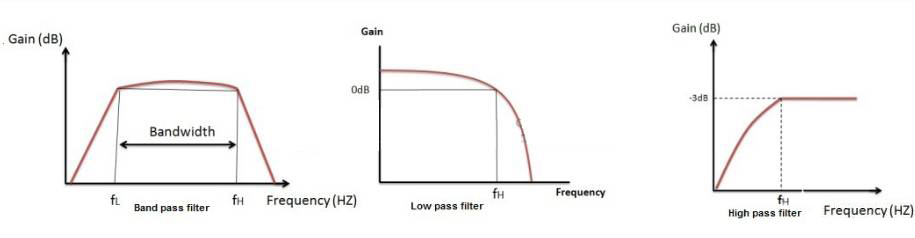
有源带通滤波器

根据品质因数，有源带通滤波器分为宽带通滤波器和窄带通滤波器。品质因数也称为“质量因数”。通过级联高通滤波器和低通滤波器与放大组件，便可获得带通滤波器。

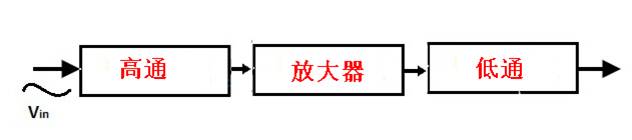
这些高通和低通滤波器之间的放大器电路将提供隔离并提供电路的所有电压增益。两个滤波器的截止频率值必须保持最小差异，但如果此差异非常小，则可能存在高通和低通级相互作用的可能性。因此，为了使这些截止频率具有适当的电平，放大电路是必要的。

有源带通滤波器的电路图如下所示：

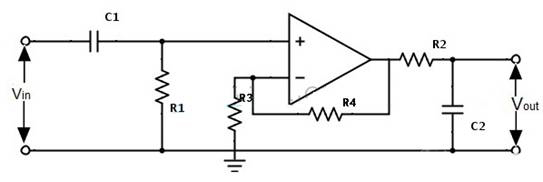
1、宽带通滤波器

如果品质因数的值小于10，则通带很宽，这种带通滤波器称为宽带通滤波器。在此滤波器中，高截止频率必须大于低截止频率。它在设计中使用了两个放大元件（运算放大器）。

首先信号将通过高通滤波器，该高通滤波器的输出信号将趋于无穷大，因此趋于无穷大的信号最终被提供给低通滤波器。

这样，低通滤波器将使高频信号低通。当高通滤波器与低通滤波器级联时，得到简单的带通滤波器。为了实现这个滤波器，低通和高通电路的顺序必须相同。

通过级联一个一阶低通和高通可为我们提供二阶带通滤波器，并通过级联两个一阶低通滤波器和两个高通滤波器形成一个四阶带通滤波器。

由于这种级联，电路产生了低品质因数。一阶高通滤波器中的电容器将阻止来自输入信号的任何直流偏置。而在二阶滤波器（高+低）的情况下，两个阻带的增益滚降为±20dB/十倍频。所以高通和低通滤波器必须是一阶的。

类似地，当高通和低通滤波器处于二阶时，两个阻带处的增益滚降为±40dB/十倍频。

带通滤波器的电压增益表达式为：

|V输出/V输入|=[Amax* (f/fL )] / √{[1+(f/fL)²][1+(f/fH )²]}

它是通过高通和低通滤波器的单独增益获得的，高通和低通滤波器的单独增益如下所示。

高通滤波器的电压增益：

|V输出/V输入|=[Amax1 * (f/fL)] / √[1+(f/fL)²]

低通滤波器的电压增益：

|V输出/V输入|=Amax2 / √[1+(f/fH )²]

Amax=Amax1* Amax2

其中Amax1是高通级的增益，Amax2是低通级的增益。

宽带滤波器的响应如下所示：

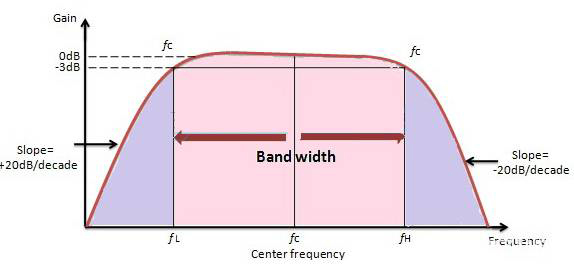
2、窄带通滤波器

如果品质因数的值大于十，则通带较窄，通带的带宽也较小。这种带通滤波器称为窄带通滤波器。

它仅使用一个有源组件（运算放大器）而不是两个，并且此运算放大器处于反相配置。在这个滤波器中，运算放大器的增益在中心频率fc处最大。

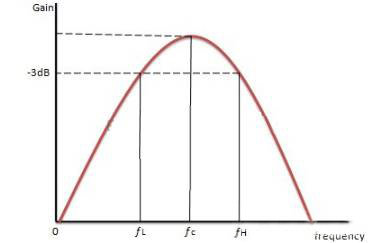
输入被施加到反相输入端，这表明运算放大器处于反相配置。该滤波器电路产生窄带通滤波器响应，如下图所示：

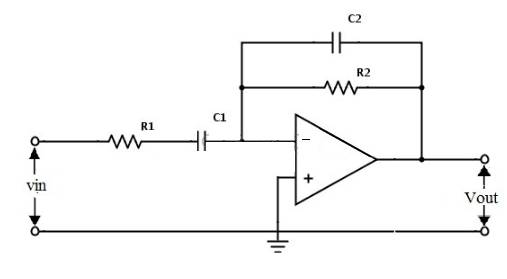
上述滤波电路的电压增益为AV=– R2/R1。

滤波电路的截止频率为：fC1=1/ (2πR1C1 ) 和f C2=1/(2πR2C2 )。

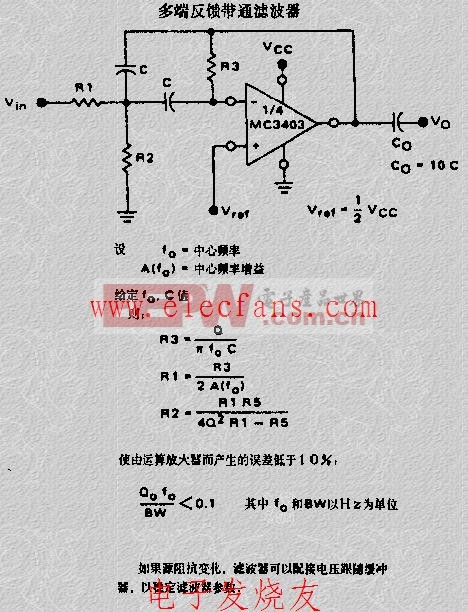
多反馈有源带通滤波器

该滤波器电路根据滤波器的负反馈产生调谐电路。这种多重反馈的重要优点是，在中心频率处的最大增益没有任何变化的情况下，可以改变截止频率的值。截止频率的这种变化可以通过电阻R3’来完成。

通过考虑下面的有源滤波器电路，这里将改变的电阻值视为R3’，将改变的截止频率值视为fc’，那么可以将新的电阻值等效为：R3′=R 3 (fc/fc′)²。

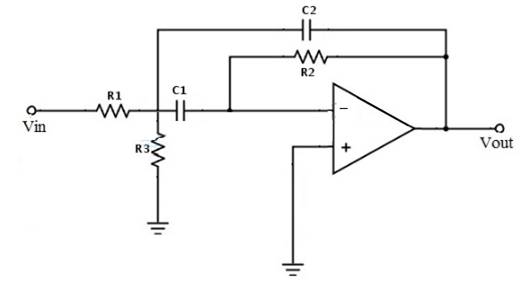
它由两条反馈路径组成，由于这种多反馈路径，它也被称为“多反馈带通电路”。该电路产生一个无限增益多反馈带通滤波器。由于该电路，品质因数值最多可增加到20。

fc=1/√(R 1R 2C 1C 2 )

Q=fc/带宽 = (½){√[R2 /R1 ]}

Amax=-R2/2R1

R1=Q/{2πfcCAmax}

R2=Q/πfcC

R3=Q/{2πfcC(2Q² – Amax)}

中心频率“Amax ”处的增益必须小于 2Q²。即：A最大值 < 2Q²。

其中，fc=截止频率，单位 Hz、C=电容，(C 1=C 2=C)、Q=品质因数、Amax=最大增益。

有源带状滤波器的频率响应如下图所示：

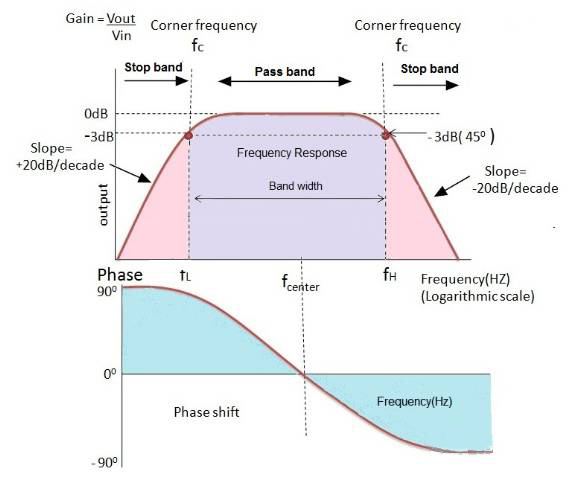
它有两个中心频率，一个是高通滤波器，另一个是低通滤波器。高通滤波器的中心频率必须低于低通滤波器的中心频率。

带通滤波器的中心频率是上下截止频率fr2 =fH *fL的几何平均值。

滤波器的增益为20 log (Vout /Vin ) dB/Decade。幅度响应类似于低通和高通滤波器的响应。响应曲线取决于级联滤波器阶数。

归一化的中频为fr =1。例如考虑两个截止频率为300Hz和900Hz，则滤波器的带宽为300Hz-900Hz =600Hz。

品质因数

品质因数取决于通带的带宽，品质因数与带宽成反比。这意味着如果带宽增加，品质因数会降低，如果带宽减少，品质因数会增加。

Q=fc/带宽

对于宽带通滤波器，品质因数较低，因为通带宽度较高。对于窄带通滤波器，品质因数很高。选择性和非选择性取决于通带的宽度。

这个品质因数也与阻尼因数（）有关。如果阻尼系数值越大，输出响应的平坦度也越高。这等同于如下：

ε=2/Q

对于不同的品质因数值，二阶带通滤波器的归一化增益响应为：

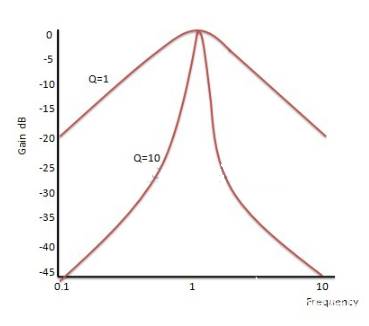
通过上图，可以清楚地看出，更高品质因数的选择性更高。

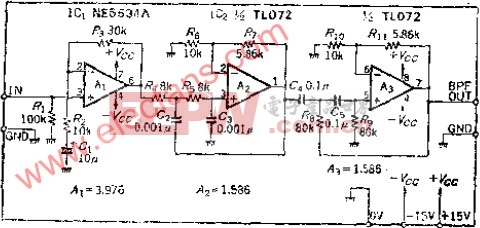
有源带通滤波器示例

这里考虑无限增益多反馈有源滤波器电路，其谐振频率为1.5 kHz，最大电压增益为15，品质因数为7，然后计算元件值。

对于电阻器：

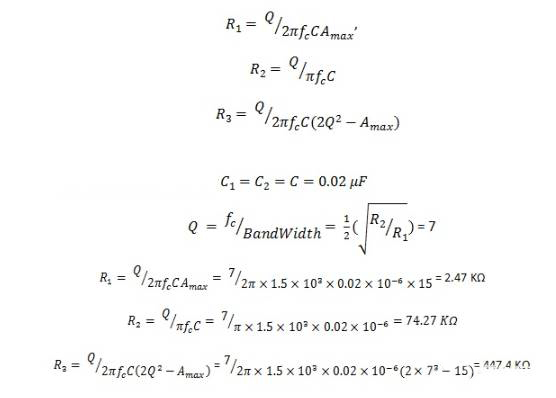
如果改变的电阻值为R3’，改变的截止频率值fc’=2 KHz，那么可以将新的电阻值等同于如下：

R3’=R3 (fc /fc’)2=447.4(1.5/2)2=251.66Ω。

因此，只需采用所需的频率，就可以计算出新的电阻值。

总结

简单来说，有源带通滤波器是一种频率选择滤波器，用于电子系统中，用于将某个特定频率的信号或位于某个频率“频带”内的一系列信号与所有其他频率的信号分离