有源前端整流器

介绍针对电动汽车充电器的最佳SiC功率拓扑和调制决策的设计技巧，利用指导拓扑和调制决策，有助于消除不可行选项，转而关注那些可能表现良好的选项。

▎引言  ▎

电动汽车的蓄电池充电器需要在电网连接和蓄电池之间进行电流隔离。因此，电动汽车充电器几乎总是有两个级：一个高电能质量整流器，将AC转换为DC；然后是DC-DC转换器，利用高频变压器进行电流隔离。

SiC FET和二极管的高开关频率可以满足使用“旧的”和简单的电路拓扑的充电器要求，而这种拓扑在硅基开关器件中是不切实际的。例如，用于单相整流的图腾柱功率因数校正器（TPPFC）和用于三相整流器的无处不在的两电平电压源逆变器（2L-VSI）。

本文概述了许多三相整流器选项中的一些，简要介绍了调制选项，以及功率半导体损耗的比较。

▎拓扑选择  ▎

假设我们需要为400或480 VAC线路RMS设计一个22 kW的三相整流器，也称为有源前端整流器（AFE）。这意味着需要功率因数校正，但功率流可以是单向的。成本、谐波失真、效率、尺寸和重量是重要的设计标准。为了实现低谐波失真，需要进行有源功率因数校正。

对于任何有单相PFC经验的人来说，三个独立的助推器可能是一个有吸引力的选择。图1显示了许多可能的实现方法中的两种。

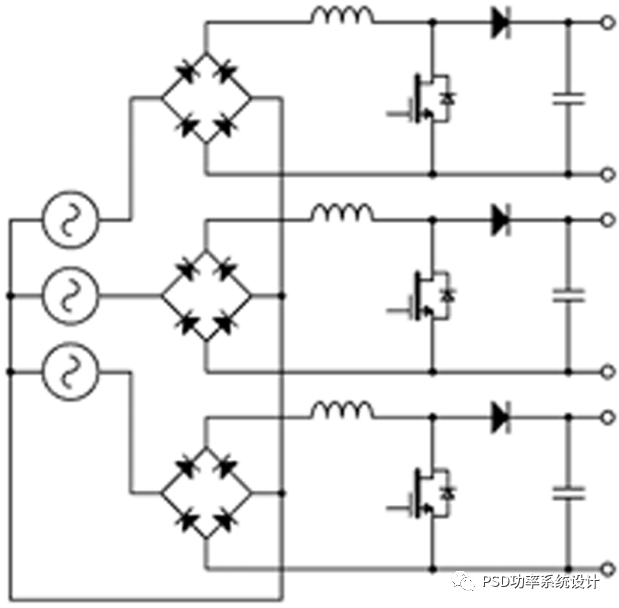
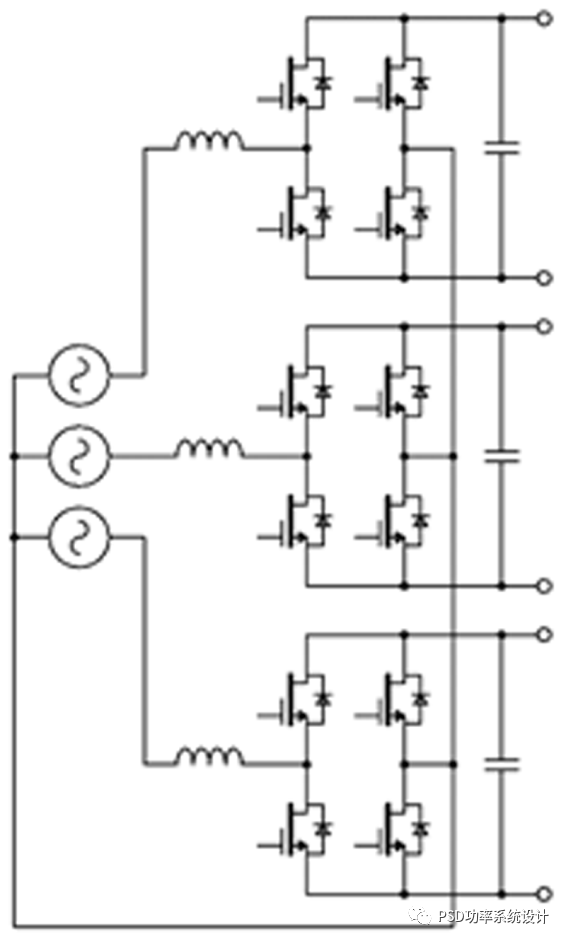
图：1（a）三PFC，（b）三TPPFC

在电动汽车充电器中，每个升压器（booster）必须向单独的隔离DC-DC转换器供电，这些转换器输出是并联在一起的。这是一种可行的方法。通过消除输入二极管电桥并使用图腾柱拓扑，可以略微提高传统PFC升压器的效率，其示例如图1（b）所示。

12个功率半导体（一些可能是二极管而不是FET）使得这种方法不那么吸引人，因为在三电平拓扑中，相同数量的器件可以产生成本更低、更小的线路滤波器的好处。

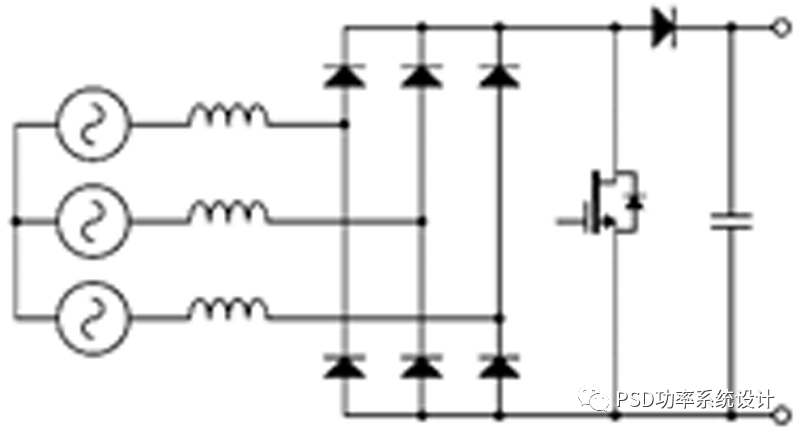
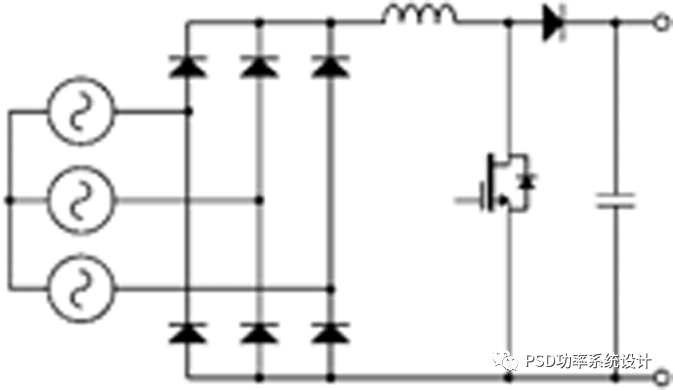
图2：两种简单但不可行的拓扑：（a）二极管桥后的升压电路，（b）带升压电路的线路电感

由于高失真、尺寸、重量和成本，三线电感器之前的三相二极管电桥已经过时。如图2（a）所示，在三相二极管电桥之后添加一个升压开关和二极管，将由于开关频率比线频率高得多而缩小电感器。然而，由于失真，这只在某些情况下有效，因此不可行。

在图2（b）中，与传统单相PFC一样，二极管电桥后的单个升压电路会产生不可接受的谐波失真，约为30%。因此有必要积极塑形每相电流。实现这一点的许多方法之一是在每个线路电感器和分离DC链路之间添加背对背的FET，如图3（a）所示。这是三电平Vienna整流器的一种流行变体，它对所有SiC功率半导体都是高效的[1]。

Vienna整流器中的SiC二极管具有480 VAC线路输入，额定电压为1200 V，但开关损耗可以忽略不计。每个二极管在FET开关频率下与其对应的FET对进行换向。每个FET必须只阻断一半的DC链路电压，因此开关损耗低，650 V或更高的FET额定电压是可以接受的。

电流在Vienna整流器中完全成形，从而产生极低的谐波失真。作为三电平滤波器，线路滤波器的成本、尺寸和重量更低。功率流是单向的。为了支持双向功率并略微降低传导损耗，在三相电桥中用1200 V FET代替二极管，如图3（b）所示。

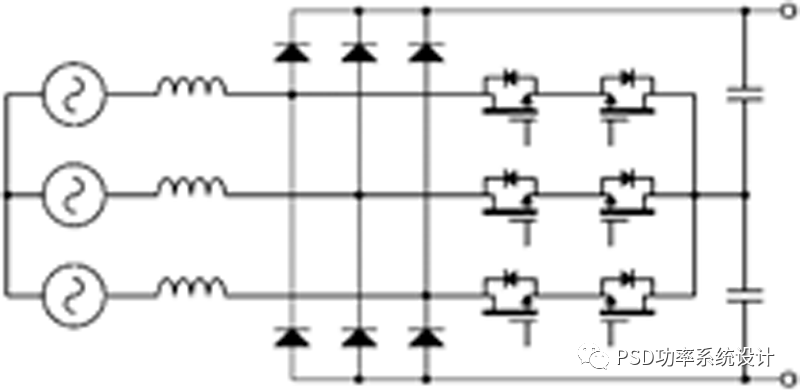
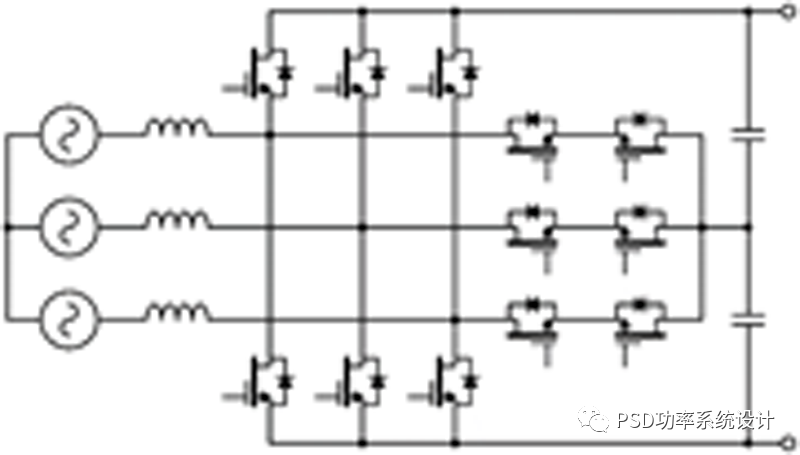
图3：（a）改进的Vienna整流器，（b）三电平TNPC

这是三电平晶体管中性点钳位拓扑（3L-TNPC）。它可以在任何功率因数下工作，但作为整流器工作时，桥式FET的开关损耗可以忽略不计。3L-TNPC的PWM策略是将电桥和钳位FET对反相。与Vienna整流器一样，每个钳位FET仅阻断一半的DC链路电压，因此开关损耗较低。

在某些情况下，额外的FET和栅极驱动器超过了三电平线路滤波器所降低的成本。通过简单地消除钳位FET，就可以解决这一问题，从而产生无处不在的两电平电压源逆变器（2L-VSI）。2L-VSI只有6个FET，但它可以在任何功率因数下完全塑形线电流，因此它支持双向功率流，谐波失真低。

可以使用三电平NPC和ANPC拓扑，但在这种应用中，它们没有TNPC的优势，尤其是SiC FET的高性能。使用更高的DC链路电压时，需要更多这类拓扑，例如在具有1500 VDC输入的太阳能系统中。

▎调制方法  ▎

以下推导主要针对2L-VSI，但这些调制方法也适用于3L-TNPC和其他逆变器拓扑。

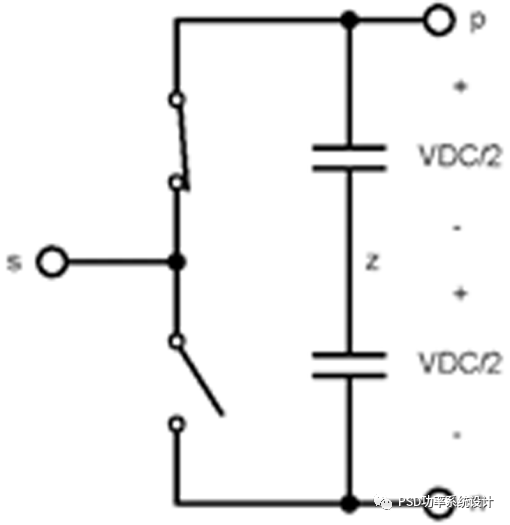
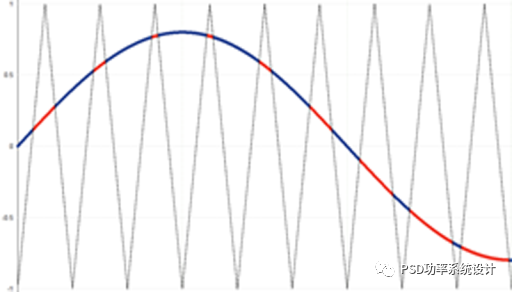
图4：（a）半桥，（b）正弦三角形参考和载波波形

在半桥中，使用正弦三角调制的DC链路中点z（可能是虚的）的最大输出电压为V_DC/2，如图4（a）所示。无论相脚（phase leg）的数量如何，这都是正确的，因为每个脚都通过正弦三角调制独立于其他脚。换句话说，相脚之间没有切换协调。这意味着三相四线连接很容易使用，如图5（a）所示。

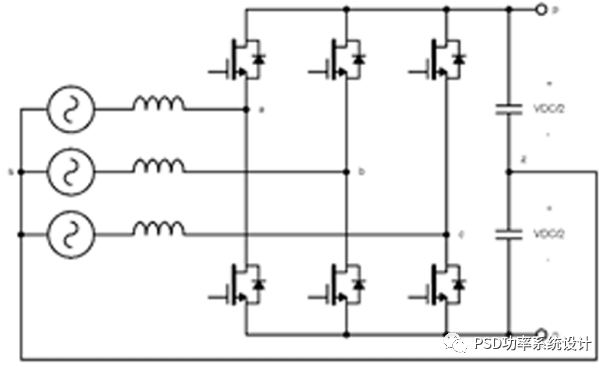
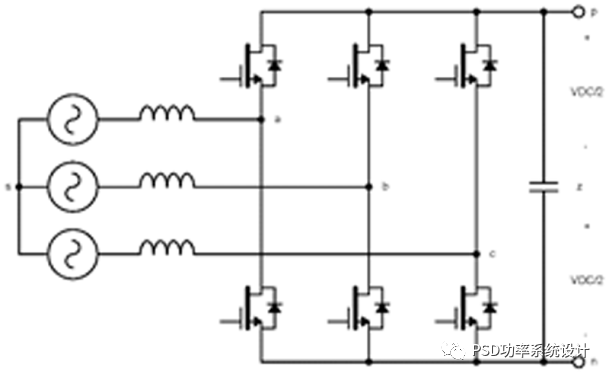
图5：2L-VSI（a）带4线连接，和（b）带3线连接

在三线连接中，如图5（b）所示，DC链路中点z通常是假想的，因为薄膜电容器可以在不串联的情况下支持DC链路电压。车载EV充电器中4线连接的一个优点是能够在单相输入或三相输入下工作。对于单相输入，两相脚的工作原理与TPPFC相同。

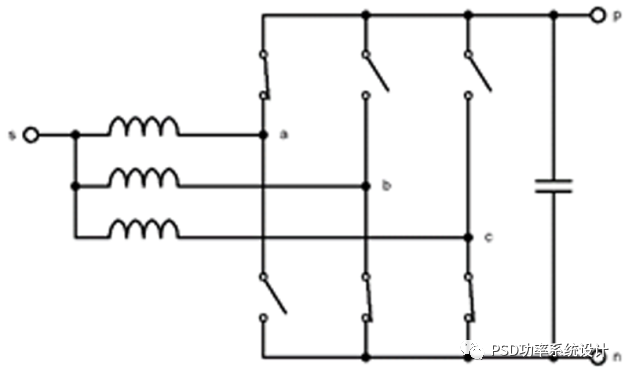
图6：三相分压

我们需要知道AC到DC链路电压的范围。推导最大线间电压的一种方法是分压。当A相顶部开关打开，B相和C相底部开关打开时，A相的线到中性点电压，即图6中A点到s点的电压是DC链路电压（电容器两端电压，从p到n）乘以A相阻抗除以B相和C相并联阻抗（A相的一半）加A相阻抗。

因此，A相线到中性点的电压为  。这是负载或电源上可以产生或支持的最大电压。在电感器和s点之间插入平衡的三相电压源会产生相同的结果，因为电压总和为零。利用开关在每个相脚中始终处于相反状态（忽略死区时间）的简单PWM策略，我们通过将开关组合与每个相脚的AC端子处的电压向量相关联来创建空间矢量图。

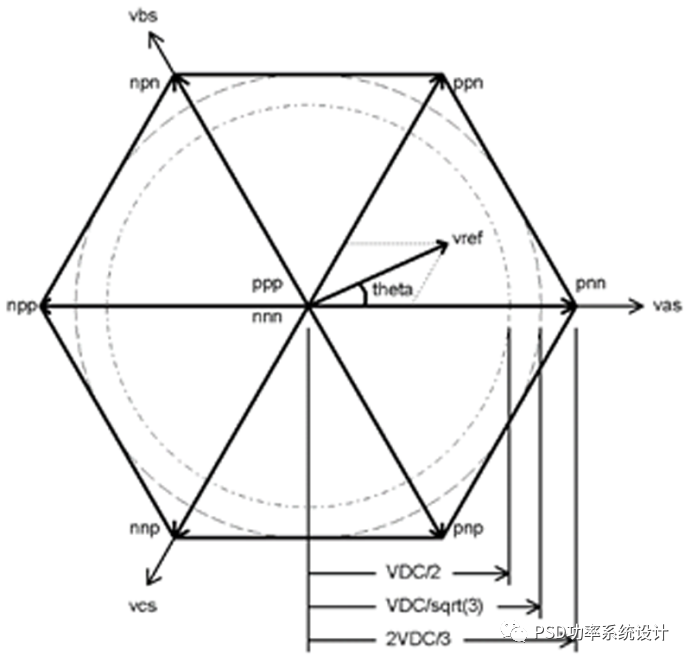
图7：（a）2L-VSI的空间矢量图，（b）红色为正弦三角采样波形，蓝色为空间矢量，绿色为60°C不连续调制的采样波形

图7（a）中的开关状态由三个字母（或数字）指定，每个相位一个，字母p或n（或数字1或0）对应于图6中的DC链路轨。例如，A相顶部开关接通，B相和C相底部开关接通由pnn指定。2L-VSI共有8个矢量：6个最大电压矢量和2个冗余零矢量。线电压通过平均参考电压附近的矢量所花的时间来近似旋转（rotating）参考电压vref。

驻留时间可以使用如图7（a）所示的空间矢量图或如图7（b）所示比较参考和载波波形来计算。关于这方面的文献有很多[2]，但本文只涉及正弦三角、常规空间矢量（以下简称SVM）和60°不连续调制（电压峰值钳位，也称为DPWM1）。

为了避免削波（脉冲跳跃）和谐波失真的跳跃，参考向量长度被限制在图7（a）中的内圆（对于正弦三角形），以及SVM和DPWM1中的较大圆。SVM和DPWM1电压增加幅度的物理原因是什么？是因为这些调制方法（以及包括三次谐波注入在内的其他调制方法）导致节点s的平均电压相对于DC流链路以3倍基频（线）频率“摆动”。

这是通过在相位之间共享零状态时间实现的。节点s的移动电位“展平”了SVM和DPWM1参考波形，允许对于给定DC链路电压系数为  的较高线路电压与正弦三角相比。另一方面，每个相位通过正弦-三角调制独立于其他相位，允许节点s的电压相对于DC链路固定，而无需改变调制，从而实现可选的4线连接。

SVM和DPWM1具有降低EMI和更宽输入/输出电压范围的优点。SVM和正弦三角在功率半导体中具有几乎相同的传导和开关损耗。DPWM1的优点是，在每个基本线路周期内，在60°间隔内两次钳位DC链路轨，从而降低开关损耗。这种优势往往超过传导损耗的增加，即使是在快速开关的情况下。

正弦三角和SVM可以很容易地用于Vienna整流器。可以想象，由于二极管电桥，Vienna整流器固有地具有不连续PWM，SiC二极管中几乎为零的开关损耗进一步增强了PWM。可以对钳位FET使用更有限的不连续PWM，但其中的开关损耗已经相当低，因此这里不予考虑。

关于实现，与使用空间矢量图计算PWM驻留时间相比，在微控制器中实现SVM和DPWM1参考波形（如图7（a）所示）与三角形载波波形（PWM计数器）的比较可能更容易。如果同时发生跳变，DPWM1波形中的跳变不会导致线路电流失真，因为相电压总和始终为零。这可以通过写入“影子”PWM寄存器来实现，这些寄存器随后会更新到同一时钟沿上的有源PWM寄存器。

▎效率比较  ▎

使用在线FET-Jet计算器工具估计功率损耗。对于每个拓扑，相脚或相位的数量为3。以下条件适用。

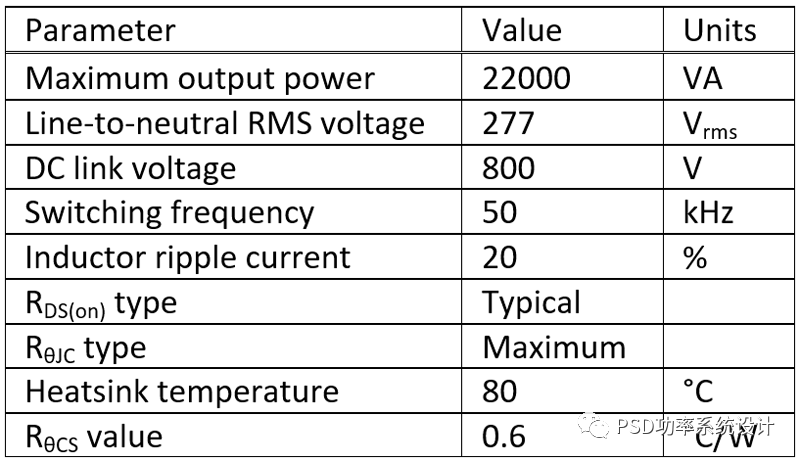
表1：功率损耗计算参数

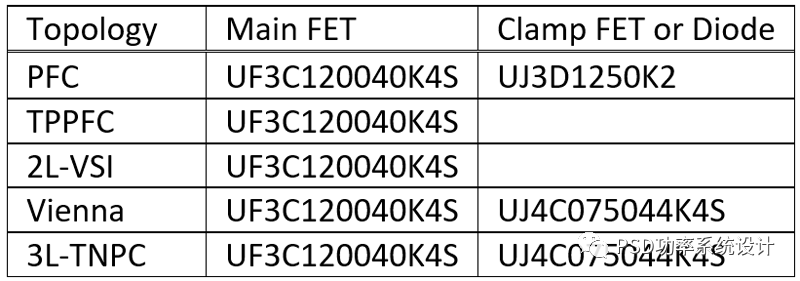
表2：功率半导体选择

表2功率半导体选择中的器件选择考虑了成本。在某些情况下，使用不同的器件选择，可以稍微降低功耗。因此，提供了许多器件号，因此可以根据各种应用要求优化权衡。

对于PFC，在线计算器忽略了硅基线路整流器的损耗，因为这些损耗不是由UnitedSiC提供的。因此，进行了自定义计算，包括Diotec Semiconductor典型的1200 V单相整流桥KBPC5012FP的损耗。结果如图8所示。

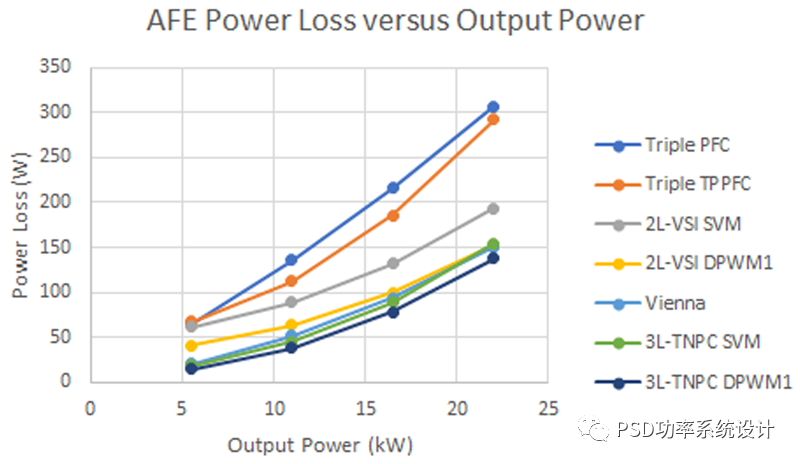
图8：功率损耗比较

毫不奇怪，三PFC的损耗最高，其次是TPPFC。这主要是因为电流路径中的半导体数量。接下来是采用空间矢量调制的2L-VSI。这也是意料之中的，因为总共只有6个功率半导体，更高的效率通常需要更多的硬件。

一个有趣的例外是，与2L-VSI中的正弦三角或SVM相比，不连续PWM显著降低了功率损耗。Vienna整流器优于配备DPWM1的2L-VSI，但在全功率下，它们的功率损耗大致相等。带有SVM的3L-TNPC的功率损耗仅略低于Vienna整流器，而DPWM1的效率明显更高。

这些结果只需几分钟就能收集到。可以进行进一步的优化，预计计算结果与实际结果之间会有一些差异是合理的。撇开免责声明不谈，这些趋势是明确的，有助于指导拓扑和调制决策，至少有助于消除不可行的选项，转而关注那些可能表现良好的选项。

www.unitedSiC.com

参考文献

J.W. Kolar, T. Friedli, “The Essence of Three-Phase PFC Rectifier Systems”, Proceedings of the 33rd IEEE International Telecommunications Energy Conference (INTELEC 2011), Amsterdam, Netherlands, October 9-13, 2011

C. Grahame Holmes, Thomas A. Lipo, “Pulse Width Modulation for Power Converters, Principles and Practice”, IEEE Press and Wiley-Interscience, ISBN 0-471-20814-0, Copyright 2003

注：Jonathan Dodge是UnitedSiC P.E.

* 本文由PSD翻译，并转自PSD