一种基于位宽调节的低功耗DCT电路设计*

*基金项目：自然科学基金 61874023、61534002，中央高校基本科研业务费ZYGX2018J030

作者简介：钱亦端 (1994—)，男，硕士研究生，研究方向：DCT电路设计。

贺雅娟 (1978—)，女，副教授，研究方向：专用集成电路与系统、超低压超低功耗数字集成电路设计等。

0   引言

随着多媒体服务的发展，视频和图像已经成为了人们生活中不可或缺的一部分。然而，由于其庞大的数据量，视频和图像信息的传输会消耗大量功耗，缩短移动设备电池的寿命。为了解决这个问题，一般在图像传输之前使用图像压缩系统对数据进行压缩，而离散余弦变换（DCT）通常作为这个系统的核心。但是，DCT是运算密集型的运算，电路直接实现会占用大量的硬件资源，引入较大的功耗，影响整个系统的稳定性。如何降低运算的复杂度成为了DCT研究的重点，一些DCT的快速算法相继被提出。

考虑到电路实现中乘法器的硬件复杂度，目前关于DCT的研究主要集中在去乘法的DCT上。去乘法的DCT大致可以分为3类：基于分布式算法（DA）的DCT^[1]，基于坐标旋转数字计算方法 （CORDIC）的DCT^{[2, 3]}，基于常系数乘法的DCT^[4]。

①基于DA的DCT通过查找表和累加器来计算DCT中的内积。但是它在电路的实现中需要额外引入ROM，无法有效地控制面积。

②基于CORDIC的DCT利用CORDIC算法，使用迭代的移位和加法运算来实现蝶形三角函数运算。CORDIC算法可以实现较高的精度，然而更高的精度往往需要更多的迭代次数，导致运算量的增加。

③基于常系数乘法的DCT将运算的乘法系数表示整数二进制的形式，然后通过对应的移位和加法运算取代原本的乘法运算。

相较于前面的两种算法，基于常系数乘法的DCT可以实现更为理想的面积和功耗，本文对于DCT的研究正是利用了这种方法。同时，人眼具有有限的感知能力，无法察觉到图像发生的细微变化，即在一定范围内的图像精度的损失是允许的。因此，可以根据DCT的性质和输入图像的特性，在DCT的设计中引入近似计算，在不显著降低图像质量的前提下简化运算过程。

本文提出了一种基于位宽调节的低功耗DCT电路设计。该方法利用DCT的能量集中特性，通过调整乘法系数的位宽将运算资源集中在具有较高优先级的输出上，从而简化DCT的结构，减小电路实现的硬件开销。对比传统的DCT，提出的近似DCT以图像质量的少量损失为代价，有效地减少了电路的面积和功耗。

1   DCT原理

二维DCT将输入的图像数据从空间域变换到频域。通常在进行DCT运算之前，我们首先需要将一幅完整的图像分割为若干个8×8的像素块。二维DCT的公式如下所示：

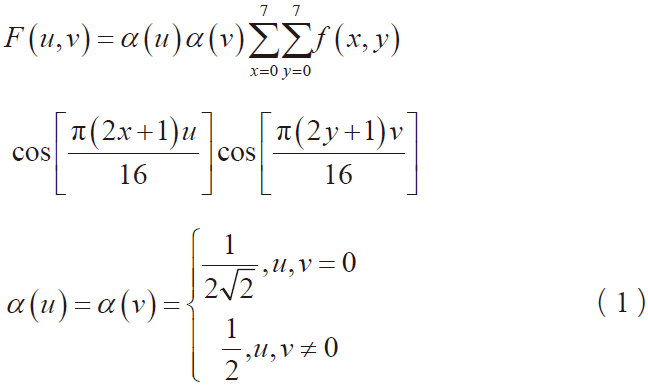
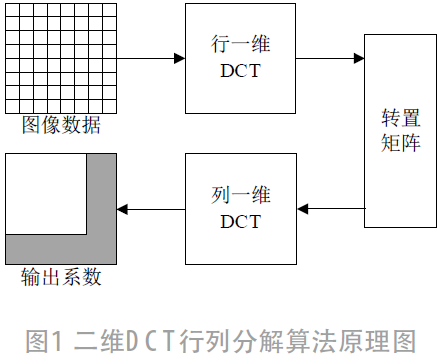
其中，f (x, y)代表输入的8×8的像素块，x和y表示像素的空间坐标，F (u, y)代表输出的变换后频域系数，u和v是系数的频率值，取值范围为0~7。考虑到二维DCT的运算复杂度，我们通常使用行列分解算法，将二维DCT分解为2次一维DCT，如图1所示。先将输入的图像数据进行1次行一维DCT运算，将中间的运算结果转置后，再进行1次列一维DCT运算。

一维DCT的计算如下所示：

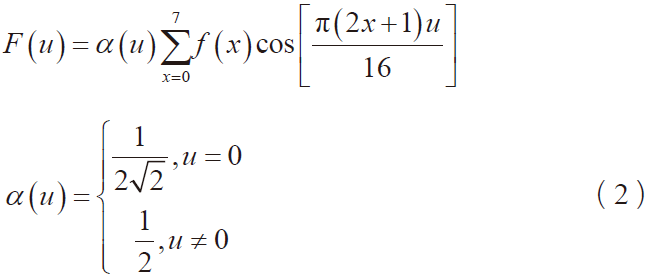
其中，f(x)代表输入的行矢量，F(u)代表输出的列矢量。将其表示为矩阵的形式，并对上式的输出进行奇偶分离，

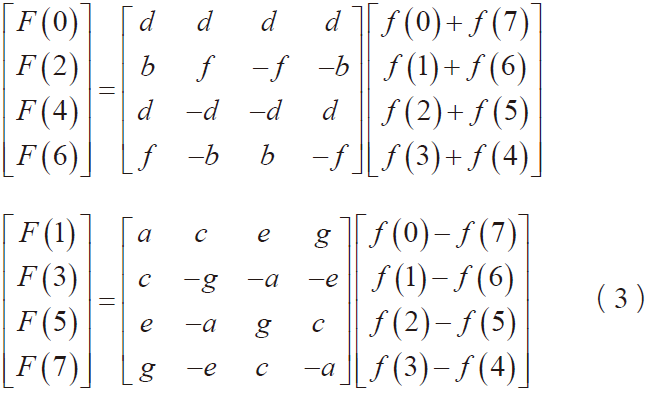
其中，a~g为常系数，令，a=s1,b=s2, c=s3, d=s4, e=s5, f=s6, g=s7。

2   基于位宽调节的DCT设计

2.1 近似DCT设计

采用基于常系数乘法的DCT的设计方法，将系数a~g表示为移位后的二进制形式，如表1所示。

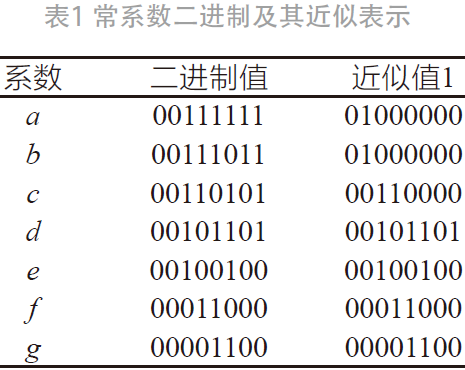
通过这种方法，原本的乘法运算可以使用加法和移位运算实现。例如，对于输入为in的常系数乘法a·in，逻辑上等价于：

即，系数a的乘法运算等价于5次移位运算和5次加法运算。同时，在系数的二进制表示中，非零位的个数决定了加法和移位次数。为了简化运算的复杂度，对表1的系数进行近似。从表中可以得到，除了参与直流系数F(0)运算的d，其余近似系数的非零位个数至多不超过2个，对应的加法运算次数不超过1次。需要注意的是，在上述的设计中，为了在电路实现过程中能满足精度，我们将原本二进制小数向左移位后表示为8位整数的形式，需要在运算的最后对输出进行截位补偿。

2.2 系数的位宽调节

DCT具有能量集中特性，输出的能量主要集中在低频部分^[6]，即输出的有效数值集中于低频区域，高频区域在数值上趋于0，对最终的图像质量影响较小。因此，减小高频输出的位宽能在不显著影响图像质量的前提下，有效降低中间运算的复杂度。由于DCT的运算中存在共享的中间结果，直接对输入的位宽进行调整会对整个运算的精度产生影响。为此，我们可以通过常系数的位宽调节实现输出位宽的降低。基于这个思路，本文对近似系数进行了重新设计，如图2所示。相较于表1的近似值1，近似值2具有更高的近似程度，实现了低4位的归零。利用这个特点，我们可以对近似值2的位宽进行调节，仅保留有效的高4位。

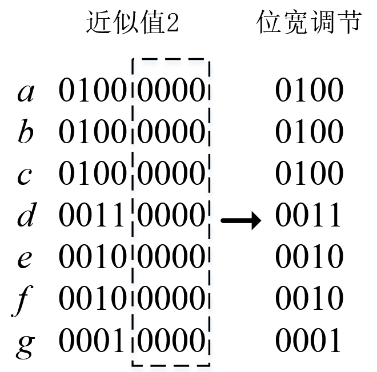
图2 系数位宽调节方案

结合DCT的能量集中特性，对高频输出F(4), F(5),F(6)和F(7)的常系数乘法运算采用位宽调整后的近似系数，对于低频输出F(0), F(1), F(2)和F(3)采用近似值1。结合式(3)，得到了图3所示的近似DCT结构。

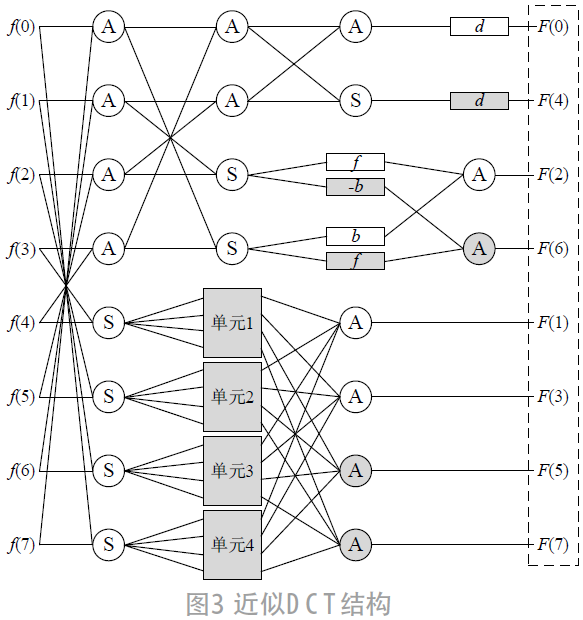
其中，虚线框表示输出的截位补偿，符号A和S分别代表加法器和减法器，方框内的系数表示通过移位器和加法器实现的近似常系数乘法运算，单元1~单元4对应于式(3)中第2个系数矩阵第4列~第1列的乘法运算。阴影部分标注了受到位宽调节影响的低位宽运算单元。

由此可见，系数的位宽调节不但可以降低对应的常系数乘法所需的位宽，还可以减小后续加法器消耗的硬件资源。

对提出的近似DCT结构进行硬件复杂度分析，完成一维DCT运算需要37个加法器和27个移位器，相较于传统DCT的64个加法器和46个移位器，硬件复杂度降低了约40%。

3   实验结果与分析

本小节评估了提出的近似DCT电路的性能，并将它与传统的DCT、基于CORDIC的DCT[3]和其它的近似DCT^[4]进行了对比分析。在图像处理领域，通常使用峰值信噪比(PSNR)来反映图像的精度。一般我们认为PSNR值越大，电路的精度越高，其定义如下:

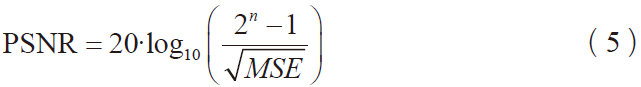
其中，MSE代表原图像和还原图像之间的均方误差，n表示像素的比特数，对于灰度图的取值为8。为了测试在不同环境下电路的精度，我们选取了8幅具有不同特征的图像，包括Lena,、Airfield、Bridge、Plane、Peppers、Barbara、Crowd和Goldhill，如图4所示。

(a)	(b)
(c)	(d)
(e)	(f)
(g)	(h)

图4 仿真实验图：(a)Lena (b) Airfield (c) Bridge (d) Plane (e) Peppers (f) Barbara (g) Crowd (h) Goldhill

使用Verilog HDL描述上述的DCT电路，输入图像数据，通过VCS对电路的功能进行仿真，结合Matlab还原图像并计算平均PSNR。然后，为了得到电路的功耗和面积信息，将时钟约束设置为100 MHz，使用综合工具DC在0.18 μm的CMOS工艺下对设计进行综合，得到的实验结果如表2所示。

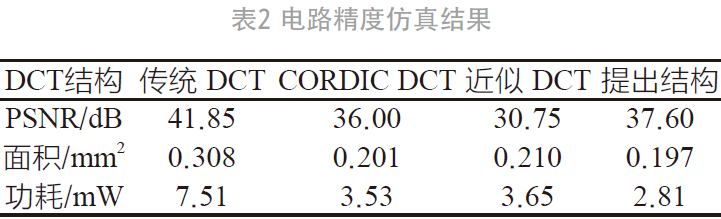
从表中可以得到，传统的DCT具有最高的精度。这是因为传统的DCT是相对精确的结构，而其他的DCT都为了实现更小的面积和功耗对电路进行了不同程度的近似。同时，对比其它近似DCT，提出的DCT电路借助更小的面积实现了更高的PSNR，在CORDIC DCT和近似DCT的基础上进一步下降了约20%的功耗，使之能够适用于一些低功耗的工作场合。

4   结论

本文提出了一种基于位宽调节的低功耗DCT电路设计。利用DCT的能量集中特性，我们通过乘法系数的位宽调节减小了高频输出中间运算的位宽。仿真结果显示，对比传统的DCT，提出的近似DCT的PSNR只下降4.3 dB，但其面积减小了36.0%, 功耗降低了62.6%。相较于其他的近似DCT，提出的设计在其他电路性能指标均存在一定优势的前提下，降低了约20%的功耗，充分说明了本文的设计存在的优越性。

参考文献：

[1] YU S, SWARTZIANDER E E.DCT implementation with distributed arithmetic[J]. IEEE Transactions on Computers,2001,50(9):985-991.

[2] JEONG H,KIM J,CHO W K.Low-power multiplierless DCT architecture using image data correlation[J].IEEE Transactions on Consumer Electronics,2004,50(1):262-267.

[3] LEE M,YOON J,PARK J.Reconfigurable CORDICBased Low-Power DCT Architecture Based on Data Priority[J].IEEE Transactions on Very Large Scale Integration (VLSI) Systems,2014,22(5):1060-1068.

[4] KAUSHAL V,Garg B,JAISWAL A,et al.Energy Aware Computation Driven Approximate DCT Architecture for Image Processing[C].2015 28th International Conference on VLSI Design, Bangalore, India, Jan. 2015:357-362.

[5] PARK J,ROY K.A low power reconfigurable DCT architecture to trade off image quality for computational complexity[C].2004 IEEE International Conference on Acoustics, Speech, and Signal Processing, Montreal, Que., Canada, May 2004:V-17.

[6] LI Z,PENG S,MA H,et al.A Reconfigurable DCT Architecture for Multimedia Applications[C].2008 Congress on Image and Signal Processing, Sanya, China, May 2008:360-364.

（本文来源于《电子产品世界》杂志2020年9月期）