基于单相SVPWM的可变死区算法
光伏发电的核心技术是逆变技术。在单相逆变器中,为了防止逆变桥上下两个功率开关管直通,通常需要在功率管工作期间加入一段固定死区时间[4-6]。固定死区时间会带来输出电压幅值和相位的偏差,随着开关管频率的提高,误差累积效应会导致输出电压波形的畸变[7]。
本文引用地址:http://www.amcfsurvey.com/article/202203/431628.htm本文首先通过分析单相SVPWM(空间电压矢量脉宽调制)原理,建立起单相SVPWM 的调制波波形,然后采用干扰观测器估计出补偿电压并换算成开关管导通时间作为死区时间加入调制波中有效矢量组的导通时间中。实验结果表明该策略可以使单相逆变器输出电压畸变率降低,输出波形更优的正弦波。
1 单相SVPWM原理及实现
单相空间矢量调制技术主要是由三相空间矢量调制技术推导而来。在三相逆变器中将6 个功率开关管组成的3 组桥臂定义为开关函数![]() ,其中Si =1 代表每相上桥臂导通,下桥臂关断,而Si = 0 则代表每相上桥臂关断,下桥臂导通。总共有8 组基本电压矢量组,基于伏秒平衡的原理可以计算出8 组基本电压矢量组合形成标准的圆形旋转矢量磁链所需要功率开关管导通时间。基于三相SVPWM 技术的思想,以下进行单相SVPWM 的详细推导。
,其中Si =1 代表每相上桥臂导通,下桥臂关断,而Si = 0 则代表每相上桥臂关断,下桥臂导通。总共有8 组基本电压矢量组,基于伏秒平衡的原理可以计算出8 组基本电压矢量组合形成标准的圆形旋转矢量磁链所需要功率开关管导通时间。基于三相SVPWM 技术的思想,以下进行单相SVPWM 的详细推导。
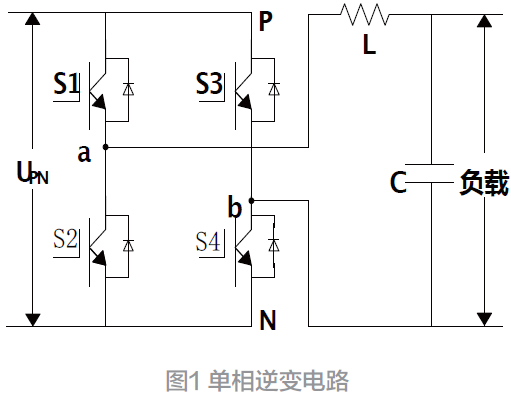
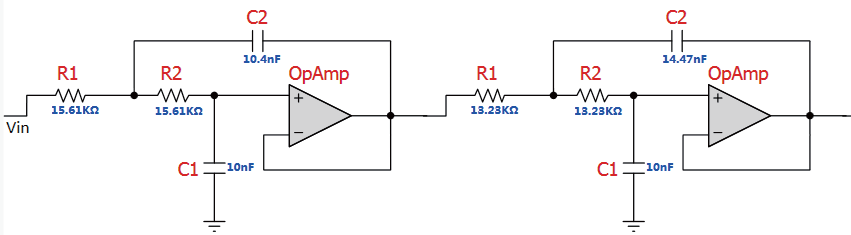
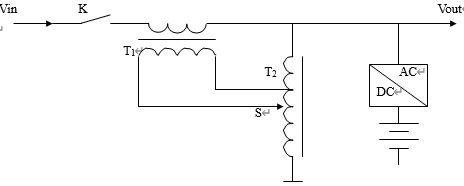
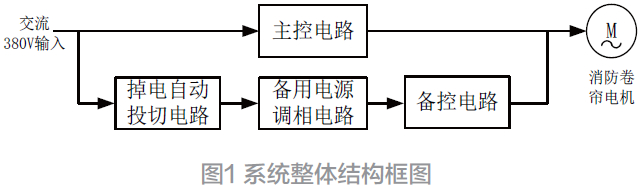
如图1所示单相逆变电路,其中a、b 两点的输出电压用Uab表示,则交流侧输出电压矢量可表示为

采用“1”代表功率开关管的导通,“0”代表功率开关管的关断。通过对S1、S2、S3、S4 的开通与关断进行组合分析可得单相逆变电路中共有4 种开关状态,与之相对应的输出电压矢量如表1 所示。
由表1 可知,分别有两种有效状态矢量v1、v2和两种零状态矢量v0、v3。根据空间矢量调制原理,通过将4 个离散矢量合成输出矢量Uab ,其中Uab 有0、UPN 、−UPN 三个数值。以自然基e1、e2 为基建立二维正交坐标系可得Uab 如图2 所示。
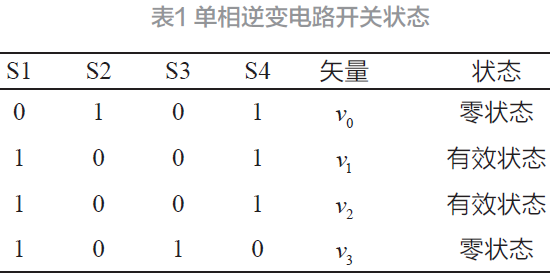
图2 单相SVPWM在自然基下的表示图
根据图2 可知,状态矢量v1、v2都在y = −x所在的直线上,取e1、e2作为基底,则矢量u 可表示为
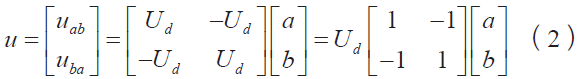
取正交基为

由矩阵变换原理可得变换矩阵为

则转换至α—β 坐标系下有
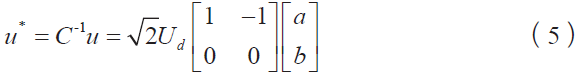
如图3 所示。
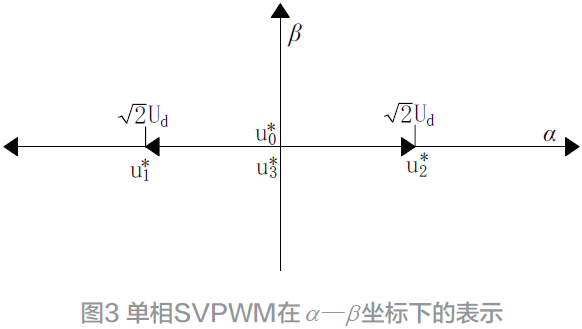
假设单相电压的有效值为Uφ ,则单相电压矢量可表示为
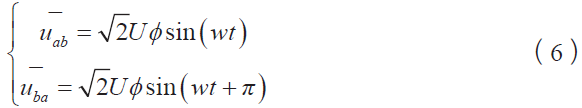
即

转换至α—β 坐标下则有
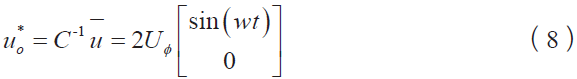
由4 组离散矢量组拟合出期望的输出电压矢量。
设定T为逆变器的载波周期,T1为有效矢量作用的时间,T0为零矢量作用的时间,由伏秒平衡的原理可得
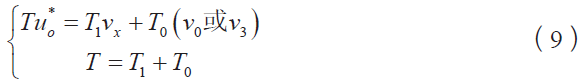
(1)当0≤wt≤π,取v2 ,则可得
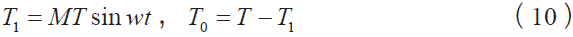
(2)当0≤wt≤π,取v3 ,则可得
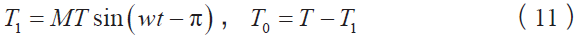
其中M 为调制比,大小为

由式可得一个调制周期内4 个开关管控制信号的通断时间长短,如图4 所示。
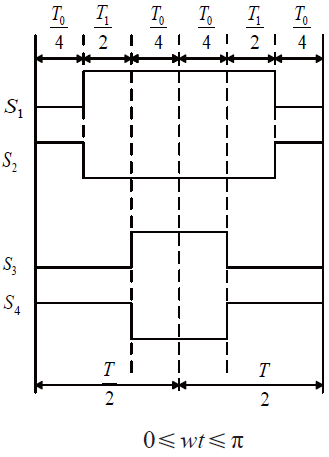
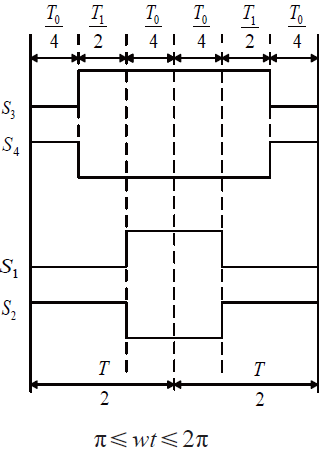
图4 单相SVPWM开关管导通时间
2 死区在线补偿原理
为了避免上下桥臂直通带来极大的短路电流,通常会对上下桥臂加入死区时间进行延迟导通,如图5 所示。
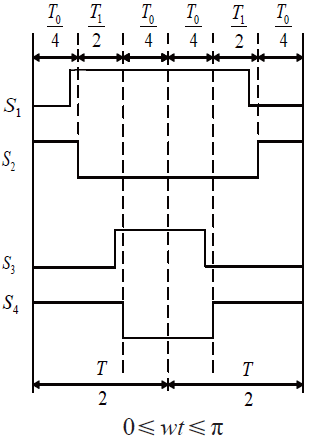
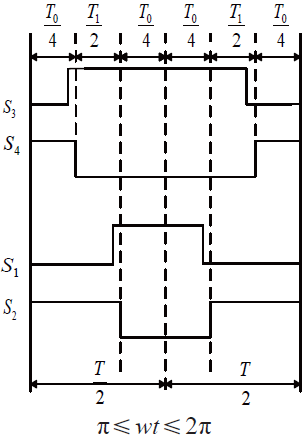
图5 加入死区的开关管导通时间
加入死区后,虽然能够防止各种非理想状况导致同一桥臂上下开关管直通,但上述死区加入会导致输出波形幅值的降低,产生严重的波形畸变。

考虑干扰电压下的系统电压方程在旋转坐标系下表达式为

一般认为当干扰电压与补偿电压相等时,则可消除死区的影响。由于系统的采样周期一般很小,属于微秒级别,故可以认为在一个采样周期内,系统的干扰电压基本保持不变,即

则当前周期的干扰电压值可用上个周期干扰电压值来进行估测,由式(12)可得
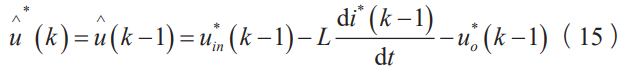
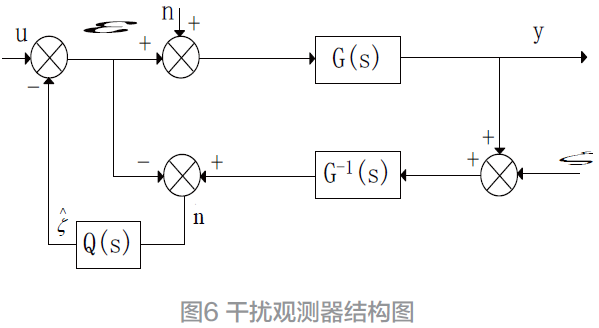
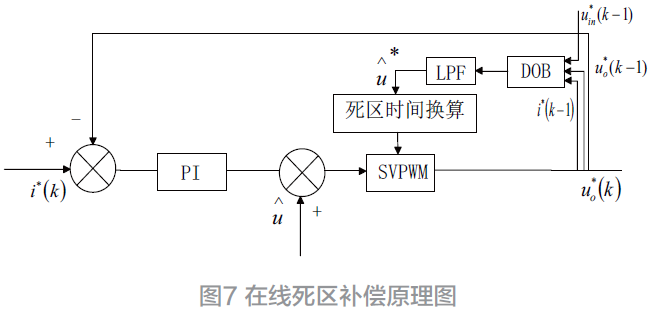
由式(15)所设计系统死区在线补偿原理图如图7所示。
3 实验与结果分析
本节中,基于TMS320F28335 的实验平台搭建了2 kW 实验样机,通过对TMS320F28335 的事件管理器进行设置,设置为连续增减计数模式,则可以产生对称的PWM 波形,可将死区补偿值直接加入比较寄存器CMPR 中进行修改PWM 脉冲宽度,达到补偿效果,其中后级 LC滤波电路中L = 0.7 mH,C = 0.15 μF。
图8 是未进行补偿的实验波形,图9 是进行死区补偿后的电压波形。
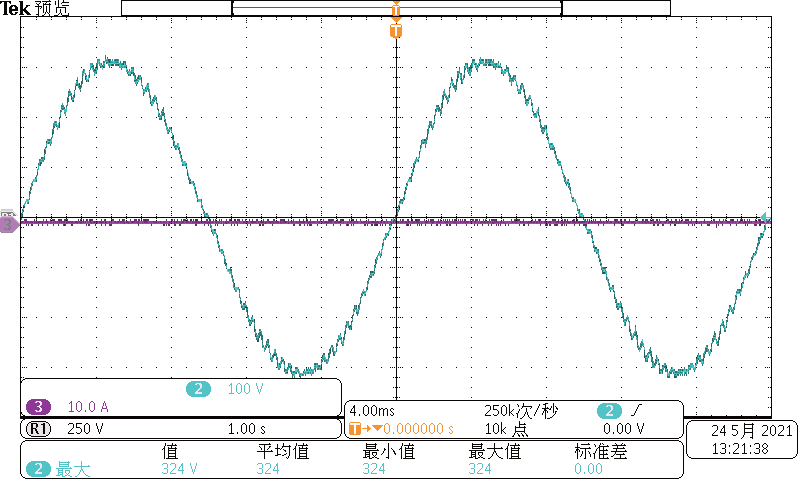
图8 未进行死区补偿的电压波形
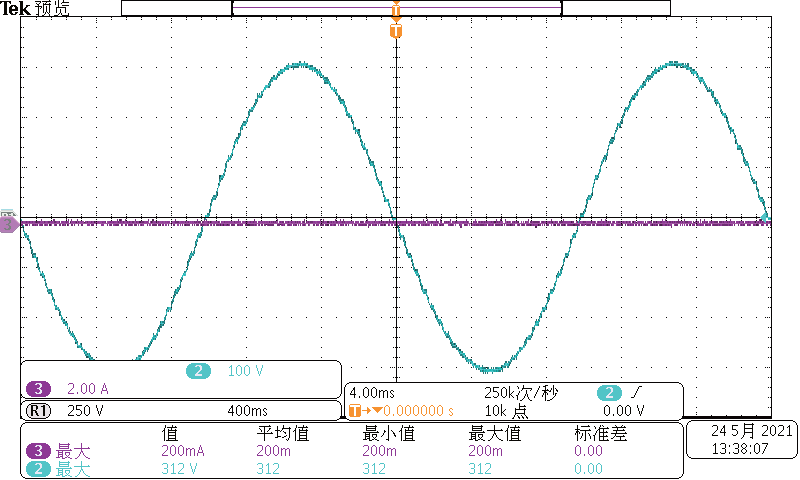
图9 进行死区补偿后的电压波形
通过图8、图9 的对比可以观察出采用死区补偿算法后的电压纹波得到明显降低,逆变器输出电压具有良好的正弦波效果。
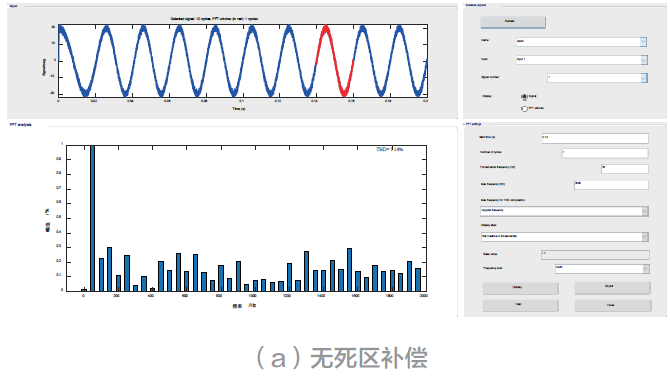
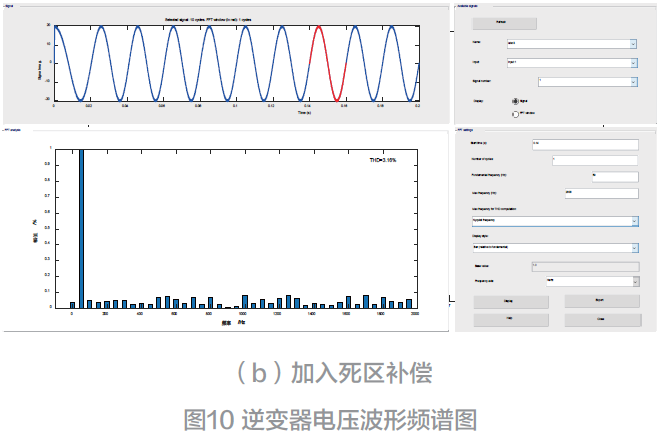
将上述逆变器输出电压波形图片导进Matlab 进行傅里叶变换分析得到图10 所示的波形,加入死区补偿算法后逆变器电压输出畸变率只有3.16%,相比没有加入死区补偿算法7.14%,降低了将近4%,表明加入死区补偿算法后有效降低了死区效应对整个系统的影响。
4 结论
本文首先通过对单相电压空间矢量法原理和产生方式进行阐述,推导出单相SVPWM 各开关管的导通时序图,针对传统死区时间的加入导致输出电压波形畸变,采用了干扰观测器对非线性干扰等因素进行在线估测并转化为死区时间作为补偿。实验结果表明该方法可以有效抑制由逆变器一系列外在非线性因素导致的电压波形畸变,改善了电压的波形,提高了系统运行的稳定性。
参考文献
[1] 方刚,杨勇,卢进军,等.三相光伏并网逆变器电网高阻抗谐振抑制方法[J].电力自动化设备,2018,38(2):109-116.
[2] 吴汪平,楚皓翔,解大,等.PI控制器参数对并网永磁直驱型风力发电系统机网相互作用的影响[J].电力自动化设备,2017,37(10):21-28.
[3] Liu Xing, Wang Dan, Peng Zhouhua. Cascade-free fuzzy finite-control-set model predictive control for nested neutral point-clamped converters with low switching frequency[J].IEEE Transactions on Control Systems Technology,2019,27(5):2237-2244.
[4] 齐昕,王冲,周晓敏.一种低硬件资源消耗快速SVPWM算法[J].电机与控制学报,2014,18(4):32.
[5] 易龙强,戴瑜兴.SVPWM技术在单相逆变电源中的应用[J].电工技术学报,2007,22(9):116-117.
[6] 张阳.微电网SPWM单相并网逆变器控制技术研究[D].沈阳:沈阳工业大学,2014.
[7] 杨晓东,王崇林,史丽萍,等.级联型逆变器的统 一SVPWM方法[J].电工技术学报,2014,29(6):145-147.
[8] 刘和平,董治平,邱彬彬,等.一种低压电动汽车用 逆变器非线性因素的新型补偿方法[J].电机与控制 学报,2020,24(9):30-38.
[9] 韩坤,孙晓,刘秉,等.一种永磁同步电机矢量控制SVPWM死区效应在线补偿方法[J].中国电机工程学 报,2018,38(2):620-627.
[10] 吴春,齐蓉.PWM 电压源逆变器非线性因素迭代学习补偿[J].中国电机工程学报,2015,35(3):702-709.
(本文来源于《电子产品世界》杂志2022年2月期)




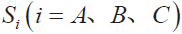

评论