基于CS-AGA-BP神经网络的房价预测分析

摘要：经过MATLAB编程对GA-BP神经网络、PSO-BP神经网络、RBF神经网络与传统BP神经网络进行精度对比；另外经过计算发现CS-AGA-BP神经网络预测精度得到提升，多次运行均方差要低于GA-BP神经网络，可以认为模型优化取得良好的效果。

1   算法基本原理

1.1 BP神经网络简介

BP（back propagation）神经网络是一种多层前馈型神经网络，其具有三层及三层以上的多层结构，每层均由若干神经元组成，相邻层间的神经元均实现全连接，而上下层各神经元间无连接。BP 神经网络分为输入层、隐含层和输出层，输入层和输出层均为一层结构，节点数目分别为自变量与因变量的数目，隐含层数不设限制，依据Kolrnogorov 定理，所有3 层的BP 神经网络均可以趋近于任意的非线性函数，因此隐含层一般取1 层，节点数目由经验函数确定。BP 神经网络按有导师的学习方式进行训练，当一对学习模式提供给网络后，网络神经元将按“输入层- 隐含层- 输出层”路径传播，输出层输出网络响应，信号误差沿“输出层- 隐含层-输入层”路径传播以逐层修正各连接权和阈值，此过程被称为“误差逆传播算法”，随着修正次数的增加，网络对输入模式响应的正确率不断提高，输出值逐步逼近期望输出。BP 神经网络示意图如图1 所示。

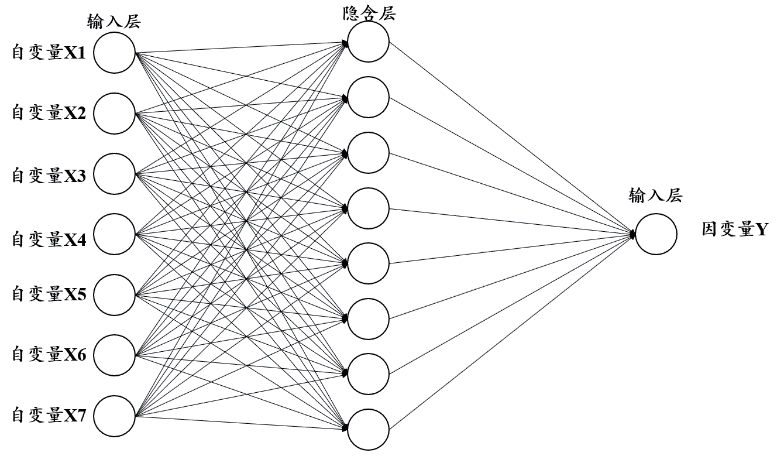
图1 BP神经网络模型结构

有监督的BP 神经网络机器学习步骤：BP 神经网络共有输入层、隐含层和输出层3 层结构，设输入层有m个变量，隐含层有l 个变量，输出层有n 个变量。输入层、隐含层和输出层的节点分别用下标g、h、j 表示；用ω gh 表示输入层和隐含层节点间的权值，用ah 表示阈值；用ω hi 表示隐含层和输出层节点间的权值，用bi 表示偏置；学习速率设置为θ 。对于输入的因变量数据x，设其目标输出值为y* ，实际输出值为y 。将选定的数据组作为样本进行网络训练，根据目标输出值与实际输出值间的误差进行正、反向传递处理。

计算正向反馈：当输入第j 个数据时，由输入层节点g 到隐含层节点h 的总输入（加权和）为：

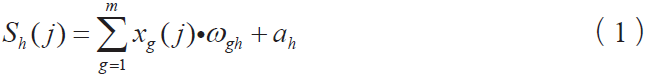
输入值和隐含层之间的关系通过激励函数——Sigmoid 函数处理，隐含层节点h 的输出值为：

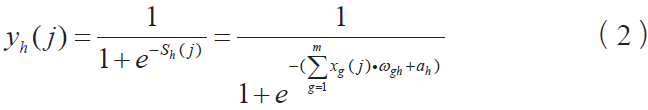
则输出层节点i 的输出值为：

因为Sigmoid 激励函数连续可微，所以训练指标函数也连续可微。

反向传递调整各层权值：为使误差尽量减小，进行网络训练时需要逐步对网络结构进行优化，采用梯度下降法对权值 ω_gh 、ω_hi 和阈值a_h 、b_i 进行更新以优化网络结构。

多次对权值和阈值进行修正后网络达到预先设定的目标误差或者最大学习次数则结束算法，网络训练成功。

1.2 遗传算法简介

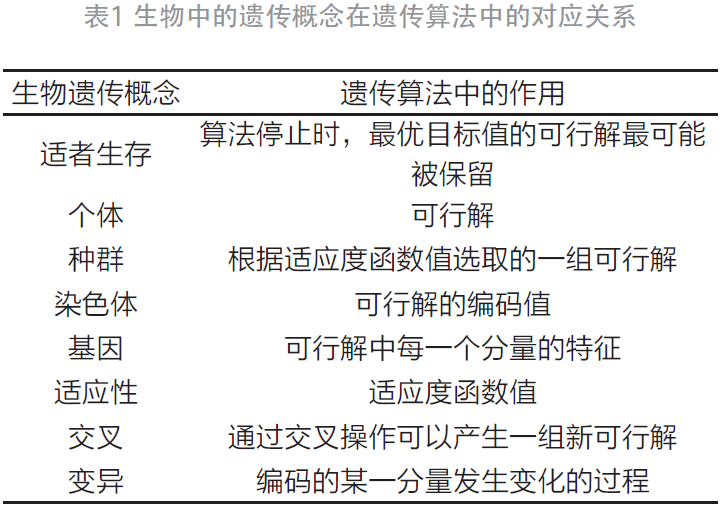
遗传算法（genetic algorithms，GA）是一种基于达尔文进化论中的自然选择原理和自然遗传机制的搜索（寻优）算法，其通过模拟自然界中的生命进化机制在人工系统中的特定目标进行逐步优化。遗传算法实质类似于粒子群算法和模拟退火等智能算法，属于群体搜索技术，其中的种群会依据适者生存的原则逐代进化，最终得到最优解或准最优解。其必备步骤包含以下几种：初始群体的产生、计算群体中个体的适应度、依据适者生存的原则选择适应度较大的优良个体、被选出的优良个体两两配对，随机交叉染色体基因并随机变异某些基因生成新群体，按此方法逐代进化，直至达到迭代次数或满足精度时终止进化，找出最优解。

生物中的遗传概念在遗传算法中的对应关系如表1所示。

1.3 GA-BP神经网络简介

传统BP 神经网络存在收敛速度慢且不利于寻求全局最优解的缺点，而利用遗传算法对原始BP 神经网络进行优化可以对BP 神经网络的权值和阈值进行更加精确的修正与优化，遗传算法的加入可以有效克服BP 神经网络容易陷入局部最优且收敛速度慢的缺陷。遗传算法部分参数需要根据经验进行设定，本研究涉及的遗传算法参数如下。

进化终止代数：进化终止代数即最大迭代次数，进化终止代数过小可能不会得到收敛的结果，过大则会造成过拟合现象。本研究选取最大迭代次数为20。种群规模：种群规模过小会造成病态基因的出现概率增大，不利于种群的进化，过大则会造成难以收敛且会浪费资源。本研究选取种群规模为10。交叉概率：交叉概率关系到种群的更新速率，过大会破坏已有的较好的种群，捕捉不到最优解，过小则不能有效更新种群。本文选取交叉概率为20%，后续采用自适应更新公式自行确定交叉概率。变异概率：变异概率关系到种群的多样性变化，变异概率过小会造成种群多样性下降过快，部分缺陷基因迅速丢失且不易修补，过大则会造成高阶模式的破坏概率增大。本研究选取变异概率为10%，后续采用自适应更新公式自行确定变异概率。利用遗传算法对BP 神经网络进行优化的具体流程如下。

1）遗传算法参数初始化：对遗传算法中的迭代次数、种群规模、交叉概率和变异概率进行初始化，迭代次数取20，种群规模取10，交叉概率取20%，变异概率取10%。

2）种群初始化：将种群的信息定义为一个结构体，存储10 个个体的适应度值和染色体的编码信息。

3）染色体编码和适应度计算：遍历10 个种群的循环，通过对各种群中每个个体的染色体随机赋值并测试其取值是否位于变量边界限制内，只保留符合条件的编码；将编码后的染色体分段，分为输入层与隐含层连接的权值、隐含层神经元阈值、隐含层与输出层连接的权值和输出层神经元阈值，将编码作为神经网络权值的赋值，设置网络的进化参数，迭代次数为20，学习率为10%，最小目标值误差为0.000 1，训练网络并进行模拟预测，将预测值与实际值之差的绝对值作为染色体对应的适应度值。

4）确定最优染色体：根据适应度值挑选出最好的染色体适应度。

5）优良个体的选择：将个体适应度值取倒数得到的数值作为其被选中的可能，将所有个体的可能值归一化处理作为概率，该值越大说明适应度值越小，该个体越优良，越容易作为父代经历交叉变异的过程，采用轮盘赌算法随机产生选择值，根据其落在哪个个体的概率区间内，将该个体作为父代并储存信息。轮盘赌规则的算法流程和转盘概率分布示意如图2 所示。

6）交叉和变异：对种群所有个体进行遍历，依据交叉概率随机选取2 条染色体并随机选择交叉位进行交叉，如果2 条染色体均可行则进行交叉，然后对新的种群信息进行存储；依据变异概率随机选取2 条染色体并进行变异，如果2 条染色体均可行则进行变异，然后对新的种群信息进行存储。

7）最优初始阈值和权值的赋值：将进化了20 代的种群的最优的基因赋值给神经网络用来预测。

8）神经网络的训练与测试：得到最优权值和阈值以及输入层、隐含层和输出层的数值后，利用训练数据对网络进行训练，然后利用后面较少的数据进行预测以及误差检验。

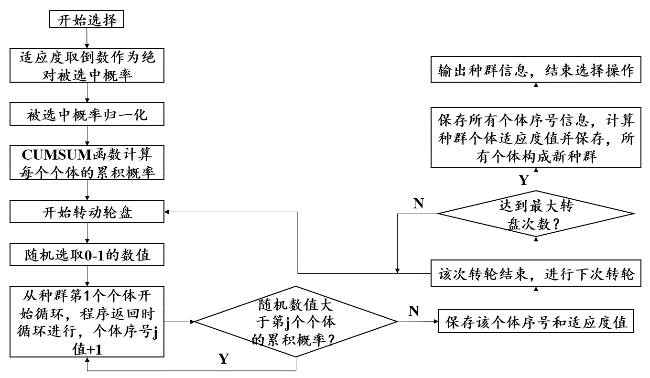
图2 轮盘赌规则的算法流程和转盘概率分布示意图

1.4 CS-AGA-BP神经网络的改进简介

为更大程度地增强BP 神经网络的优化效果，本文最终采用CS-AGA-BP 神经网络对原模型进行改进。改进分为两个方向：①交叉概率和变异概率采用自适应算法确定；②通过Logistic 混沌序列对交叉位置进行确定，并进行多基因变异。

普通遗传算法中的交叉率和变异率是人为给定的，其对遗传算法的行为和性能有着关键影响。交叉率过大，新个体产生的速度就越快，但是很容易破坏遗传模式，一些高适应度的个体结果很快就会被破坏，如果交叉率过小，个体间不能传递信息产生新个体，搜索过程会变得缓慢甚至停滞不前；变异率过大，遗传算法就变成了随机搜索算法，变异率过小就不易产生新个体。基于此，Srinvivas 等人提出用自适应遗传算法来控制交叉率和变异率的大小，使其随适应度自动改变，适应度越接近最大适应度值，交叉率和变异率就越小，为防止进化初期最优个体不发生交叉和变异，对其交叉率和变异率进行初始化，同时为了防止每一代的最优个体被破坏，通过精英选择策略将它们直接复制到下一代。交叉率和变异率的调整公式为：

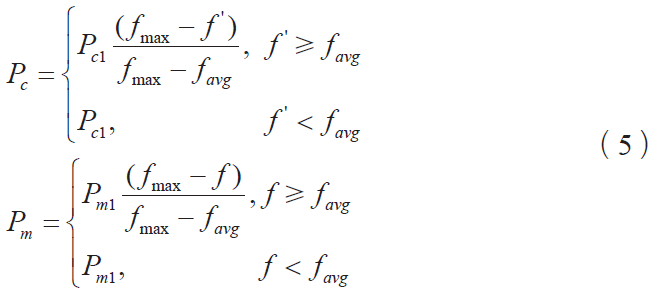
其中， f_max 为全体中最大的适应度值， f_avg 为全体的平均适应度值， f ′ 为交叉的2 个个体中较大的适应度值， f为变异个体的适应度值。该式中Pc1 取值为0.2， Pm1 取值为0.1。

遗传算法跳出局部最优解寻求全局最优解时依赖于交叉和变异操作，在交叉操作中，单点交叉（段交叉）、多点交叉和均匀交叉使用较多；变异操作一般使用Guassian 分布的随机变异来实现。许多学者采用不同方法进行变异操作以优化遗传算法，但改进效果并不明显。而混沌系统可以对交叉和变异操作同时进行改进，在交叉操作中，以“门当户对”原则进行个体配对，通过混沌序列确定交叉点，确保算法收敛精度，削弱和避免寻优抖振问题；在变异操作中，混沌序列可以对染色体中多个基因进行变异，以避免算法早熟。本文采用Logistic 混沌序列进行遗传改进，如式所示：

x(n +1) = 4x(n)[1− x(n)]   （6）

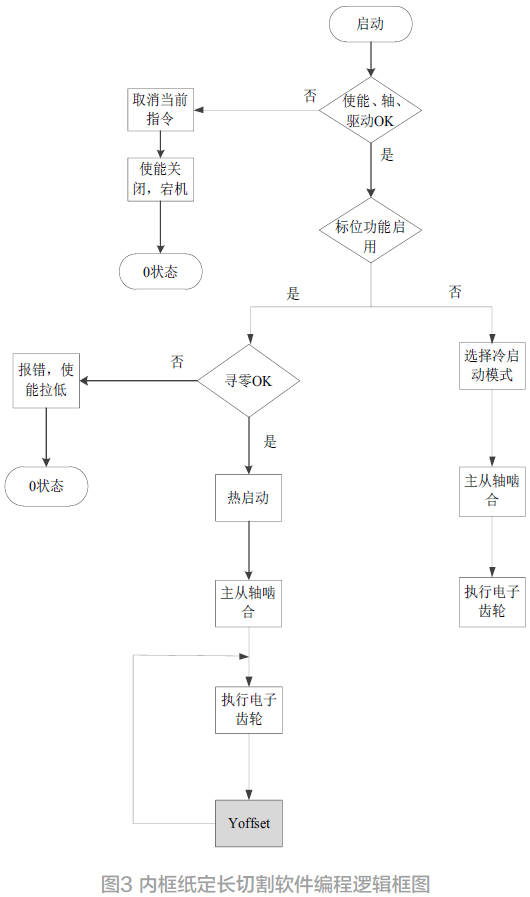
CS-AGA-BP 神经网络优化过程如图3 所示。

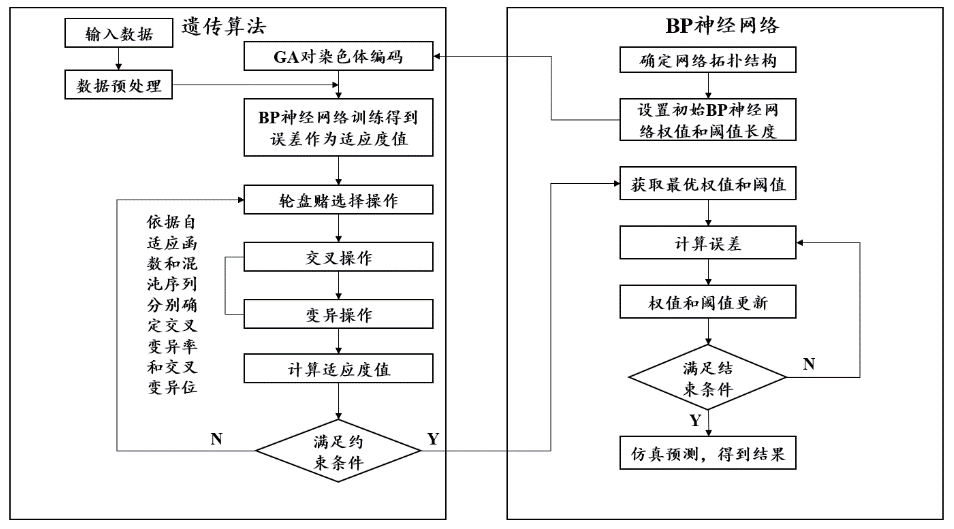
图3 CS-AGA-BP神经网络流程设计

2   算法的基本算例

2.1 数据来源与处理

本文采用数据是数据挖掘领域常用的美国波士顿房价数据集，格式为506∗14，取前 500 行数据，前80% 行用作训练数据，后20% 行用作测试数据。以前13 个指标作为模型自变量，以MEDV 作为模型因变量。

为便于将输入样本矩阵的输入范围控制在（-1，1）内以消除量纲影响，需运用MATLAB 软件中的mapminmax 函数对所有数据进行归一化处理，即：

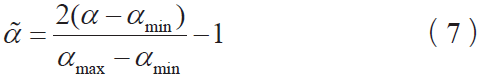
其中， α 是归一化前的变量； α_max 和α_min分别为α 的最大值和最小值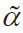；是归一化后的变量。

2.2 隐含层节点确定

神经网络隐含层节点数的选择相当重要，其对神经网络的性能影响很大，如果隐含层节点数过少，神经网络很难建立复杂的判断界，达不到合适的训练精度，容错性差；隐含层节点数过多，虽然会降低误差，提高精度，但是神经网络会趋向于复杂，从而造成训练时间增加和过拟合的情况。为确保在满足精度的前提下降低网络复杂性，即选取合适的隐含层节点数目，本研究采取以下经验函数来确定BP 神经网络隐含层的节点数目：

其中， hiddennum 是隐含层节点的数目， inputnum 是输入层节点的数目，outputnum 是输入层节点的数目，α是1~10 之间的取整调节常数。本研究中inputnum =13 ，outputnum = 1 ， hiddennum 取值范围为5~14。为了挑选出最优的隐含层节点数，此处采用均方差误差（RMSE）进行衡量，其计算公式如下所示：

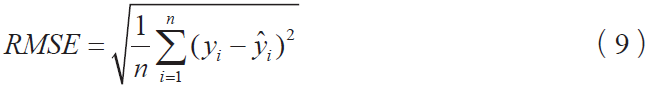
其中，n 表示样本数目， yi 表示实际房价， yˆi 表示预测的房价。

将hiddennum 从5~14 共10 个值分别代入MATLAB程序中独立运行，最后选取RMSE 最小时的10 作为隐含层节点数。

2.3 训练函数的选取

本文运用MATLAB 中newff 函数构建前馈型神经网络，newff 函数中的训练方法有基本梯度下降法（traingd）、带有动量项的梯度下降法（traingdm）和带有动量项的自适应学习算法（traingdx）等。本研究选取适用于遗传算法优化神经网络的训练函数train 进行训练。网络进化参数分别设置最大迭代次数为100，学习率为0.1，最小目标值误差为0.000 1。

3   算例的MATLAB计算结果与解析

为了便于探究GA-BP 神经网络的优化效果，本文选取PSO-BP、传统BP 和RBF 神经网络与GA-BP 神经网络的预测效果进行对比。神经网络的学习率为0.1，迭代次数为100，隐含层节点数为10。针对后100 组数据进行预测，并将预测数据与实际数据进行对比分析误差，如图4 所示。

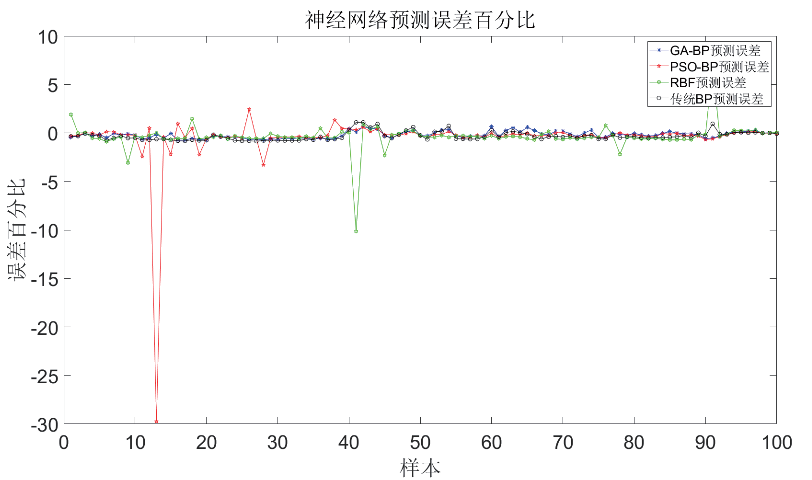
图4 四种神经网络预测的误差

通过MATLAB 计算可以看出GA-BP 神经网络和PSO-BP 神经网络预测精度较高，但是经多次运算发现PSO-BP 神经网络预测精度并不稳定。RBF 神经网络和传统神经网络误差较大，但是RBF 神经网络的优点是输出结果非常稳定。

通过CS-AGA-BP 神经网络对数据进行训练与预测，与原始GA-BP 神经网络误差百分比进行对比，如图5 所示。

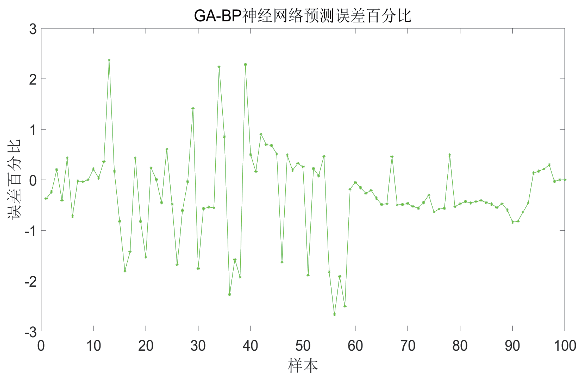
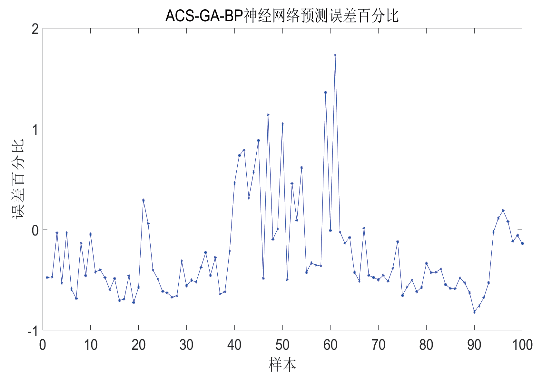
图5 GA-BP神经网络和ACS-GA-BP神经网络的误差百分比

经过MATLAB 此次计算，精度提升14.97%，虽然遗传算法对神经网络权值和阈值的更新具有随机选择性，但经过多次计算对比取平均数，CS-AGA-BP 神经网络的均方差要低于GA-BP 神经网络的均方差，误差百分比也有所减小，因此可以认为模型优化取得良好的效果。

参考文献：

[1] GENÇAY R,YANG X.A forecast comparison of residential housing prices by parametric versus semiparametric conditional mean estimators[J].Economics Letters,1996,52(2):129-135.

[2] 王宇星,黄俊,潘英杰.GA-BP神经网络在老人负性情绪预测中的应用[J].小型微型计算机系统,2020,41(8):1702-1706.

[3] 罗博炜,洪智勇,王劲屹.多元线性回归统计模型在房价预测中的应用[J].计算机时代,2020(6):51-54.

[4] 杨再宋,谢菊芳,胡东,等.基于AW-GA-BP算法的配电网设备运行环境相对湿度的预测方法及应用[J].重庆师范大学学报(自然科学版),2019,36(6):104-109,2.

[5] 惠天宇,杜尚勉,陈乐至,等.基于GA-BP神经网络的手足口病疫情预测[J].教育教学论坛,2020(38):133-134.

[6] 鲁明.基于PCA-GA-BP模型对污水BOD的预测[J].湖北汽车工业学院学报,2019,33(4):57-61,76.

[7] 罗成.基于SVD-GA-BP神经网络模型的股价预测[J].佳木斯大学学报(自然科学版),2019,37(6):988-991.

[8] 赵铭生,刘守强,纪润清,等.基于遗传算法优化BP神经网络的华北型煤田矿压破坏带深度预测[J].矿业研究与开发,2020,40(6):89-93.

[9] 司守奎,孙兆亮.数学建模算法与应用[M].北京:国防工业出版社,2015.

[10] 闵江涛,杨杰,马晨原.基于改进GA-BP网络算法的边坡力学参数反演分析[J].水电能源科学,2019,37(11):152-155.

[11] NING M,GUAN J,LIU P,et al.GA-BP air quality e v a l u a t i o n m e t h o d b a s e d o n f u z z y t h e o r y [ J ] .Computers,materials & continua,2019,58(1):215-227.

[ 1 2 ] TANG T , Y u a n S, T a n g Y, e t a l .Op t i m i z a t i o n o f impulse water turbine based on GA-BP neural network a r i t h m e t i c [ J ] . J o u r n a l o f m e c h a n i c a l s c i e n c e a n d technology,2019,33(1):241-253.

（本文来源于《电子产品世界》杂志2021年12月期）