数字温控器的高精度测温设计
作者简介:王昌世(1957-),男,硕士,高级工程师,主要研究方向为温度测量与控制。
本文引用地址:http://www.amcfsurvey.com/article/202109/427951.htm摘要:选用高精度测温芯片(Si7051)对热电偶做冷端补偿;为做温度↔电压的转换,在热电偶分度表中做高密度双向线性插值;用三线Pt100做动肩构成不平衡电阻桥来检测热电阻值;通过解析法求解Pt100的一元四次热电阻方程得到温度;使用高精度Σ-Δ且有易驱动功能的模数转换器(ADC);选用ARM Cortex-3结构的高性能32位微处理器STM32F103。综合这些技术,能使温控器测温分辨率达到0.001℃。对以上相关内容的误差分析以及在STM32F103上的编程实现是本文论述的重点。文中所述不仅是对温度测量,对其它微弱电量、非电量(如压力,重量等)信号的测量也是有借鉴作用的。
0 引言
不少温控器仍沿用传统的测温电路结构:传感器→ 滤波→ 前置放大1 → 传感器类型切换→ 前置放大2 → 再滤波→ ADC → MCU 处理。而且ADC 通常集成在MCU 中,这不仅分辨率较低(多为12 位或以下),参考电源又多不可变。此种结构元件多,噪声大,不适合高精度测控。以热电偶为例,在0 ~ 661 °C的量程内,分辨率很难超过0.1 °C。精度也难超过0.5%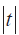 (
(![]() 是温度的绝对值温度,单位是°C )。近几年,许多IC 公司针对热电偶这样的微伏级的弱传感器信号,将上述传统测温结构集成到一起,推出了高分辨率(16 位、20 位和24 位),且有多通道的ADC,如LTC2486[1]。这为温控器的高精度测温设计提供了一种好的选择。
是温度的绝对值温度,单位是°C )。近几年,许多IC 公司针对热电偶这样的微伏级的弱传感器信号,将上述传统测温结构集成到一起,推出了高分辨率(16 位、20 位和24 位),且有多通道的ADC,如LTC2486[1]。这为温控器的高精度测温设计提供了一种好的选择。
1 高精度测温电路设计
1.1 电路结构
图1 所示是比较常规的设计,相对简单。没有了专门的信号放大、通道切换电路,滤波电路也是最简单的一阶无源RC。
1.2 温度传感器
通常,温控器要求配接2 大类传感器,热电偶(TC)和热电阻(RTD)。
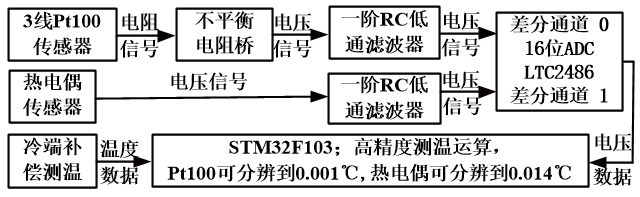
图1 温控器高精度测温电路结构
1.2.1 热电偶
最新的热电偶国际标准是2013 年版的IEC60584—1:2013,与之等同(IDT)的国家标准是GB/T1639.1—2018[4]。标准把热电偶分成多种型号(E、K、J 等),其中E 型灵敏度最高[3]。它适合做相对高精度测温。从高精度的视角,应选购1 级误差( 0.004 ×![]() ,
,![]() 是−40 ~ 800 °C温度)[4]、护套和结点隔离 [3] 但要和屏蔽层相连的E 型,以便差分连接并减少噪声。
是−40 ~ 800 °C温度)[4]、护套和结点隔离 [3] 但要和屏蔽层相连的E 型,以便差分连接并减少噪声。
1.2.2 RTD
在温控器中,这一般指Pt100,其现行的国际标准是IEC 60751:2008,等同的国家标准是GB/T30121—2013[5]。Pt100 热电阻公式如下[5]
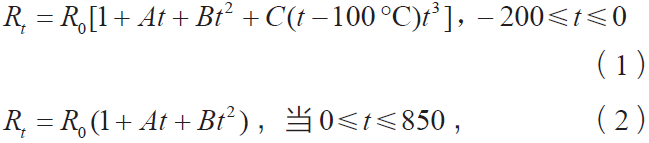
其中,t 的单位是°C ; Rt 是Pt100 的阻值; R0 是Pt100在0 °C 时的电阻( 100 Ω )[5](下同)。
Pt100 的误差(或称允差)等级分4 级[5],这里选择最高的 AA 级( ±(0.1+ 0.001 7)![]() (
(![]() 在 −50 ~ 250 °C );或A级(次高级,±(0.15 + 0.002)
在 −50 ~ 250 °C );或A级(次高级,±(0.15 + 0.002)![]() ),
),![]() 在−100 ~ 450 °C)。
在−100 ~ 450 °C)。
1.3 检测温度信号
1.3.1 热电偶
1)低通滤波
由于是电压信号,经过简单的一阶RC低通滤波就可以和LTC2486的差分输入直连[2]( CH2-CH3, ![]() ),如图2 所示。滤波器的截止频率
),如图2 所示。滤波器的截止频率
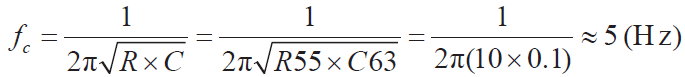 。
。
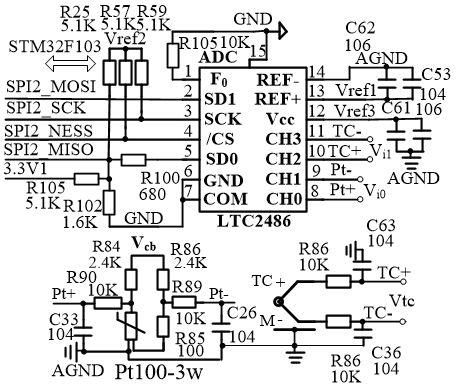
图2 温度检测及ADC电路图
2)冷端(又称参比端[4])补偿热电偶测温要解决一个冷端补偿问题。具体做法是:
①用高精度测温芯片测量TC 的冷端温度tcj[6]。
②由于温度↔ 电压的非完全线性关系,须在E 型分度表[4],用线性插值算法,把tcj 还原成电压Vcj[3]。
③把Vcj 加到TC 的输出电压Vtc 上,作为TC 的输出电压一部分。
测温芯片除用Si7051 外,还可选用TMP275(分辨率可达0.065 °C)和 ADT7410(0.007 8 °C)。
3)输出电压范围。对E 型热电偶,在−68 ~ 661 °C测温范围,查分度表[4],对应的电压( Vi )范围是−3.711 ~ 49.997 mV。为提高分辨率,可以缩小量程并加大GAIN。FS 和GAIN 的定义见1.4。
图2 中,热电偶符号中的“M”表示屏蔽端。
1.3.2 Pt100
需要把非电量的电阻变成电压信号,二线Pt100 的引线误差,不能消除,测温偏差大(r = 0.225 Ω时,约为1 ~ 1.5 °C)。三线 Pt100 不平衡电阻电桥如图 3(或图2)所示。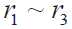 是引线电阻;
是引线电阻;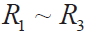 是固定电阻;
是固定电阻;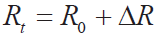 ,ΔR 表示相对R0 的随温度变化量,有正负;Vcb 是桥路电源; Vb 是不平衡时桥压。三线Pt100 电桥对引线误差是可控的。
,ΔR 表示相对R0 的随温度变化量,有正负;Vcb 是桥路电源; Vb 是不平衡时桥压。三线Pt100 电桥对引线误差是可控的。
在本温控器设计中测温范围依精度高低分二档:
①(−68 ~ 68) °C,分辨率为0.001 °C;
②(−68 ~ 466) °C,分辨率为0.007 °C。
但以下的设计论述中,仅以①为例。
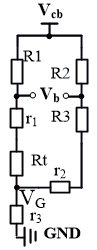
图3 三线Pt100电阻桥分析模型
1.3.2.1 电桥设计
1)电阻选择
①实测, 2 m 长的 Pt100 引线电阻 r = 0.225Ω,按20 m 以内要求, 约为2.25 Ω 。再按式(4), 要求R1 、R2 在r 千倍以上,以减少引线误差。所以取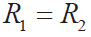 = ≥2.25 kΩ;
= ≥2.25 kΩ;
②流经Pt100 的电流( I p )要不大于1 mA [5],以控制自热。但也不能太小,否则影响电桥测阻灵敏度,实际可取I p = (1 ~ 2) mA;
③电阻越大,噪声越大[8],从这个角度看,电阻越小越好;
④电桥在0 °C 应保持平衡( Vb = 0 ),要求:
![]()
⑤考虑Vcb 用TL431 产生,所以选取 Vcb ≥ 2.5 V(见下)。综合上面4 点,R1=R2= 2 400 Ω。结合式(3)就有
![]()
R1 ~ R3用精度为 0.01%、温度系数为5×10−6 /°C的贴片电阻(批量时约0.45 元/ 个)。这个要求很重要。
2) Vcb 选择及桥压输出范围选择
由式(9)可知, Vcb 的选择与测温范围( ΔR )、桥压Vb 范围、桥路电阻选择有关。在测量范围①,当 ΔR = 26.31Ω时,若选取 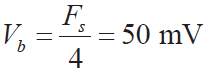 (4 就是GAIN),此时,依据式(9) Vcb = 5 000 mV,再由式(9)可得:在 −68 °C 时, Vb = −52.2 mV ,所以Vb 的范围是(−52.2 ~ 50) mV。桥压Vb 也经低通滤波( R89 、R90 、C26 和C33 ) 后进入ADC 的差分通道(CH0-CH1,
(4 就是GAIN),此时,依据式(9) Vcb = 5 000 mV,再由式(9)可得:在 −68 °C 时, Vb = −52.2 mV ,所以Vb 的范围是(−52.2 ~ 50) mV。桥压Vb 也经低通滤波( R89 、R90 、C26 和C33 ) 后进入ADC 的差分通道(CH0-CH1,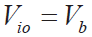 )。
)。
1.3.2.2 三线电桥误差分析[10]
先假如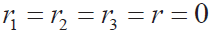 ,并依据式(6),这时桥压:
,并依据式(6),这时桥压: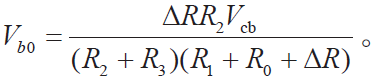
而当引线电阻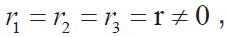 也考虑式(3),这时桥压:
也考虑式(3),这时桥压:
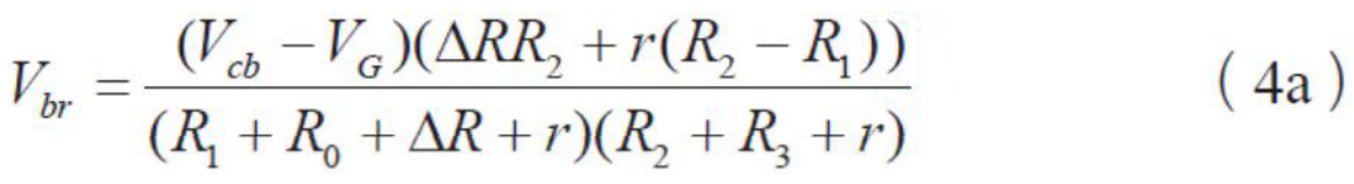
其中,
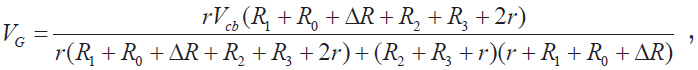
可以假设:
![]()
则Vbr 、VG 式中与r 相加项里的r 就可以忽略,因而有
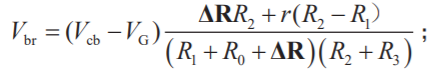
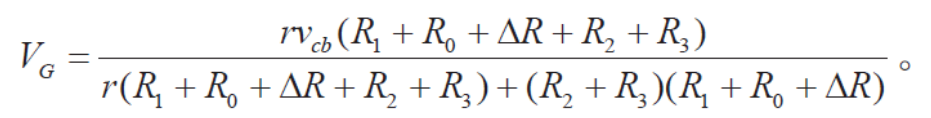
再对VG 考虑另2 个因素:
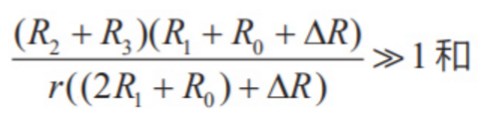
![]()
可得:

为保证测温分辨率高于0.001,要求式(4b)中

这在实际中是可以做到的。这样,式(4a)中可取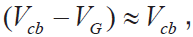 于是有:
于是有:
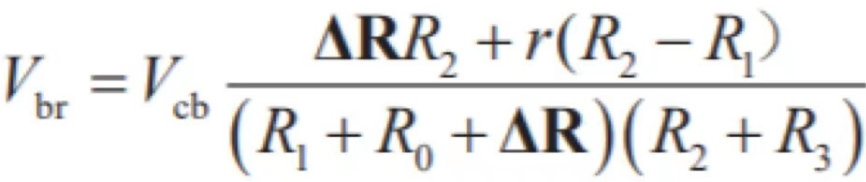 (5)
(5)
这时相对误差
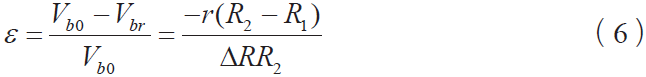
式(6)表明,① ε 可正可负,因为ΔR 、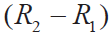 可正可负;② ΔR 越小,即温度越接近0 °C ,相对误差ε 越大;③依据式(3a),ε = 0 。
可正可负;② ΔR 越小,即温度越接近0 °C ,相对误差ε 越大;③依据式(3a),ε = 0 。
上述①,②两点和一般的感性认识一致。
现用实例说明如下:如前述, 2m 长时,引线电阻r = 0.225Ω,若ΔR = 0.195 (对Ω应温度 0.5 °C)[5],又让R1 = 2402 Ω,R2 = 2400 Ω,则由式(3),
![]()
这个相对误差很小,而且温度高于0.5 °C后,误差还会逐渐再减小。综合上述,只要满足式(3a),就能把引线电阻r影响降到![]() 以内,甚至更小(根据实际需求设计)。
以内,甚至更小(根据实际需求设计)。
而参考文献[10] 指出的分析条件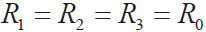 与此有差异,是否变为式(3a)更好呢?
与此有差异,是否变为式(3a)更好呢?
要特别注意的是,如果三线电阻不等(即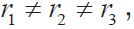 这在实际中是存在的)则会引入误差,此时,这里的三线电路也不能完好解决问题。所以在购买时要向供应商提出三线相等的要求。
这在实际中是存在的)则会引入误差,此时,这里的三线电路也不能完好解决问题。所以在购买时要向供应商提出三线相等的要求。
1.4 ADC的选择和使用
选用LTC2486(简称2486),主要是以下4 个原因[1]。
①综合分辨率高,误差小。名义上是16 位,实则17 位(包含符号位)的分辨率。理想情况下,可分辨1 μV电压。
②有2 个差分通道,正好满足一般温控器对热电偶和Pt100 的输入需求,不需外加切换电路(会引入噪声误差)。
③有内置的可编程增益放大器(PGA, 1 ~ 256 ,分8 级)。
④噪声低,误差小。
1.4.1 ADC应用电路设计
LTC2486 与传感器、STM32F103 的接口电路如图2。
1)Vcc 和REF + , REF − 电压设计
①考虑到2486 耗电低( 0.8 mW)和精度,Vcc 选
择由参考电压供电,TL431 经5 V 产生输出![]() ;
;
②定义ADC_Data 为转换数据;GAIN 为内部增益值; Vref是参考电压;Fs 是满度电压,Fs = 0.5Vref[1]。
一般忽略转换误差(偏移、非线性等),转换数据与Vref 成反比, 即ADC_Data = ![]() 。这样,Vref 越小,LSB 能分辨的电压越小。但Vref 也不能太小,不要小于400 mV [8]。这里取REF+ = 400 mV。
。这样,Vref 越小,LSB 能分辨的电压越小。但Vref 也不能太小,不要小于400 mV [8]。这里取REF+ = 400 mV。
③ 2486 的参考正电源(REF+)用较高精度的芯片(0.5%)LT6650 产生。该芯片在输入5 V 时,可调输出(0.4~4)V。
④ REF- 接地。Vref = REF + −REF− = 400 mV,Fs =![]() =200 (mV) 。
=200 (mV) 。
2)GAIN 的选取
为实现满度转换(正的转换数据达到0×10000),对热电偶,按1.3.1节,GAIN =![]() ≈ 4,取 4对 Pt100,按 1.3.2 节,GAIN =
≈ 4,取 4对 Pt100,按 1.3.2 节,GAIN =![]() = 4。注意GAIN 取值越大,噪声越大[1],ADC_Data 值波动越大。GAIN 的选择可通过控制器的按键来实现。
= 4。注意GAIN 取值越大,噪声越大[1],ADC_Data 值波动越大。GAIN 的选择可通过控制器的按键来实现。
3)与STM32F103(简称F103)的接口
通过四线SPI 与F103 接口。
①双向方式,F103 为主,2486 为从;
② F103 用的是3.3V 工作电压,而2486 用5V ,中间要有电平转换。为此,F103 的出信号(MOSI、SCK、NSS) 应设置为开路(OD), 上拉电阻为(3.3 ~ 5.1) kΩ ;而 2486 的输出信号 SDO 则应通过电阻分压到3.3 V 后连到F103 的MISO。如图2 所示。
2 编程
在IAR 7.20.5.624 版下进行。用最新在2011 年发布的3.5.0 版[9] 库函数。
2.1 F103与LTC2486接口编程
2.1.1 SPI初始化函数
1)程序
void SPI2_Init(void)
{
参照库函数编程。只是要注意设置PB13,PB15 线为复用漏极开路输出。此方式是为了在F103 与2486 间进行电平转换。
GPIO_InitStructure.GPIO_Pin_13|GPIO_Pin_15;
GPIO_InitStructure.GPIO_Mode=GPIO_Mode_AF_
OD;}
2.1.2 向2486写一个字节数据函数
1)程序
void SPI2_reg_write(u8 data)
{
① SPI2->DR = data; // 把数据放到SPI2 口的数据寄存器并发出;
② while(SPI_I2S_GetFlagStatus(SPI2,SPI_I2S_
FLAG_RXNE) == RESET);
}
2)程序注释
语句②判断写一个字节数据是否成功。类似的语句在SPI 和I 2C 的库函数中有很多,必须理解。限于篇幅,这里不多做介绍,详见参考文献[9] 和[13]。
2.1.3 从2486读出1个字节数据
直接从SPI2 口的数据寄存器读出即可。不用函数。即:b = SPI 2→ DR;b 是无符号字节变量。
2.1.4 读取2486的转换数据函数
1)算法
读取数据前,先要对2486 的工作方式进行设置(写)。不同要求,设置也不同。这里仅是一例。注意缺省值的使用。
①通常选择2486 的数据转换速率为6 次/s 。也可选12 次/s ,但这会使精度降低[1],一般不选用。
②选择转换通道。在4 个单端或2 个差分通道作选择。
③选择GAIN 值。根据1.4.1 所述,进行不同选择。
在此之后,就可以读取数据了。
④ 2486 在转换结束时会在SDO 引脚输出1 bit 低电平,它可作为转换结束标志(即EOC 信号)来判断,一般用查询方式。
⑤ 2486 每次转换后会输出3 个8 位字节数据。每个输出字节与1 个写入字节数据同步进行。所以,正确的时序是:即先写1 个字节,之后紧跟着读1 个字节;再写1 个字节,之后再读1 个字节,反复进行。如果要读的字节数多于有效的写字节,用写0 数据代替(空写)。
2)程序
Void Get2486Data(void)
{
u8 b,c,d;
③ LTC2480_CS_LOW;
④ Delay_us(30);
⑤ while((GPIOB->IDR&0x4000)!=0)
⑥ SPI2_reg_write(0xa0);
⑦ Delay_us(5);
⑧ b=SPI2->DR;
⑨ SPI2_reg_write(0x81);
⑩ Delay_us(5);
⑪ c=SPI2->DR;
⑫ SPI2_reg_write(0x0);
⑬ Delay_us(5);
⑭ 14d=SPI2->DR;Delay_us(5);
⑮ 15LTC2480_CS_HIGH;
}
注释:
语句③是让2486 的片选= 低,开始读数据。
句④是延时30 微妙,等待时序稳定(下同)。
句⑤边等待边判断转换是否结束。
句⑥是向2486 写一个字节-- 选择差分通道0。
句⑧是读一个字节数据。这是高字节,包含符号位。
句⑨是向 2486 写第二个字节 -- 选择GAIN = 4。
句⑩是读第二个字节数据。是数据的bit11~bit4。
句⑪是向2486 写第三个字节—空操作。
句⑫是读第三个字节数据。是数据的bit3~bit0。
句⑮让2486 的片选= 高,结束读数据。
2.1.5还原ADC输入电压值Vi。
1)算法
①对热电偶
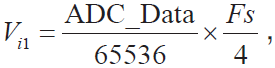
②对Pt100
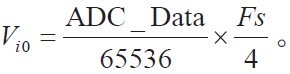
(2)程序(略)。
2.2 热电偶测温编程
2.2.1 把热电偶冷端补偿温度还原到电压程序
1)算法
参见1.3.1 2)。具体算法是:
①在 (−68 ~ 68) °C(冷端所处温度通常为环境温度),分12 段进行线性插值, 10 °C 为一个间隔(取10 的整数倍为分割点);
②设Th 、Vh 、Te 、Ve 、Tcj 、Vcj 为float(浮点)变量,分别表示每段的首点温度;首点电压;末点温度;末点电压;补偿温度;补偿电压。
③为保证插值线不间断,前一段的末点值要等于后一段首点值。
④调用函数CalculateTC_voltage(floatTh,floatTe,floatVh,floatVe,floatTcj),计算补偿电压值:
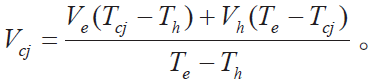
⑤把Vcj 加到热电偶的输出电压( Vtc )中,即![]() 。
。
2)程序(略)
2.2.2 由电压Vi计算温度t的程序
在(−68 ~ 661) °C的测温范围内,仍以10 °C为间距在分度表中做线性插值。
1)算法
类似上面“2.2.1-1)算法”的线性插值算法。不同的是,输入是电压Vi ,结果是温度t。具体是:①、②、③同上;
⑥调用函数CalculateTC_temperature floatTh ,floatTe , floatVh , floatVe , floatVi),由Vi 计算最终的测温值t:
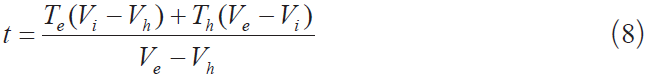
2)程序(略)
2.3 线性插值法误差分析
以220 ~ 230 °C段插值为例,显然,误差最大发生在中点225 °C。令tn ,Vn 为标准温度和电压,tn = 225 °C,Vn =15.287 (mV)[4]。这时Th = 220 , Te = 230 ,Vh = 14.912 mV, Ve = 15.664 。假设对热电偶测量电压Vi 是准确的,按式(8),计算温度
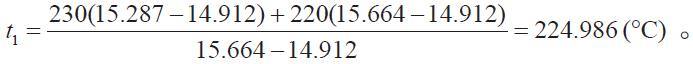
绝对误差 δ = ti− tn = 224.986 − 225 = −0.014 (°C)。满足精度要求。如需更高精度,可让插值间距更小。
除线性插值法外,也可采用计算分度函数及反函数方法[7]。
2.4 Pt100测温编程
2.4.1 把Vi0 换算成电阻Rt 的程序
1)算法
依据式(5),当满足式(3),则桥压
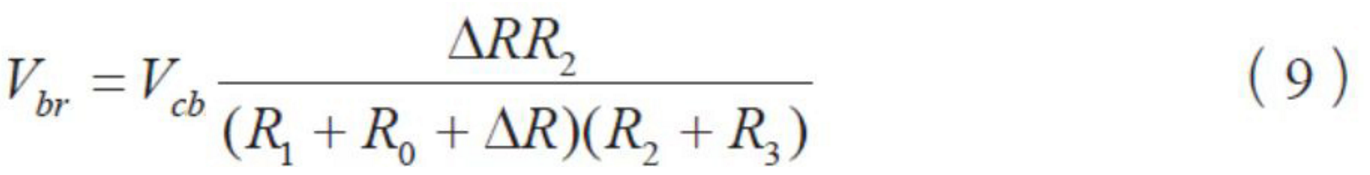
从中分离出
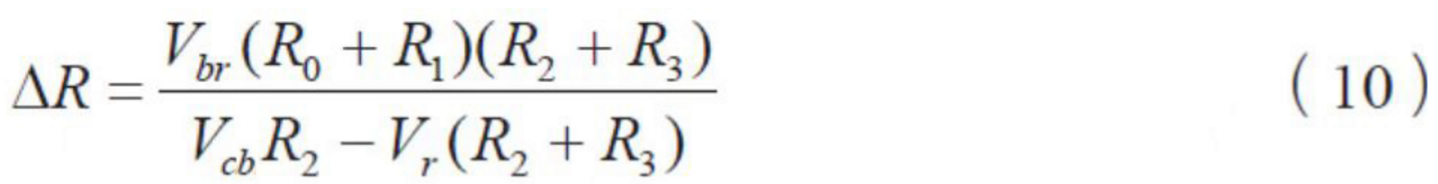
①计算ΔR
式(10)中, Vbr 即是Vi0 。该式的右边各量均已在前面给出,所以ΔR 可算出。
②计算Rt
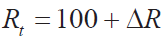
2)程序(略)
2.4.2 求解热电阻方程的程序
1)算法
将热电阻方程(1)(2)稍作变形,就有:
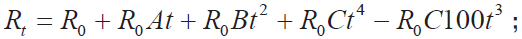
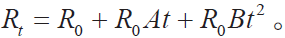
代入R0 =100和A = 3.9083×10−3 °C−1,B = −5.775×10−7 °C−2, C = −4.183×10−12 °C−4(见文献[5]),
可得当−200≤t≤0,有:
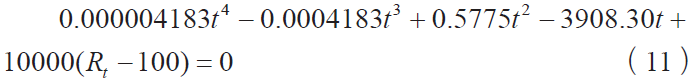
当0 < t≤850,有:
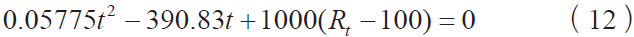
对式(11)标准形式的一元4 次方程![]() 可有如下解析方法求 4 个根[11],算法为:
可有如下解析方法求 4 个根[11],算法为:
①定义18 个float 变量:a,b,c,d,e, Δ1 , Δ2 ,Δ , t1 , t2 , t3 , t4 , y1 , y2 , y3 , y4 , y5 , y6 ,
②让a = 0.000004183,b = −0.0004183,c = 0.5775,d = −3908.30,e = Rt - 100 ;
③计算Δ1 =c2 − 3bd +12ae;
④计算Δ2 = 2c3 − 9bcd + 27ad 2 + 27b2c − 72ace;
![]()

开始求根:
⑫第一根计算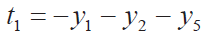 ;
;
⑬第二根计算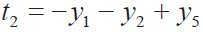 ;
;
⑭第三根计算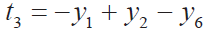 ;
;
⑮第四根计算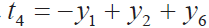 。
。
算法结束。
说明:也可以用其他方法求解此方程,如数值计算中牛顿或二分迭代法[12]。但此法更易上手。
2)程序(略)
3 温控器测温精度分析及数据记录
3.1 精度分析
测量精度通常会小于分辨率,也就是说高分辨率是高精度的基础。
3.1.1 热电偶
参见 1.3.1 和 1.4.1 节,当GAIN = 4,4× 49.99 ≈200 (mV) = Fs,此时,1LSB 对应的温度分辨值为![]() = 0.01 ( C) °,精度 [5] 为 0.004
= 0.01 ( C) °,精度 [5] 为 0.004 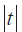 。可对 K 或其它型热电偶做类似精度分析。考虑到在同样的量程下,要达到Fs 值,需要取更大的GAIN,这将降低一些分辨率。
。可对 K 或其它型热电偶做类似精度分析。考虑到在同样的量程下,要达到Fs 值,需要取更大的GAIN,这将降低一些分辨率。
3.1.2 Pt100
①按1.4.1节,当GAIN = 4,达到满度值Fs,这时1LSB对应的测温分辨值为![]() = 0.00104 ≈ 0.001 ( ℃),精度[5]为±(0.1+ 0.0017
= 0.00104 ≈ 0.001 ( ℃),精度[5]为±(0.1+ 0.0017 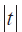 )。例如,显示值是68 °C,因为68 − 0.1− 0.0017 × 68 = 67.8864, 68 + 0.1+ 0.0017 × 68 =68.1156,所以实际温度可能是 (67.8864 ~ 68.1156) °C之间的一个值。注意,考虑电路设计的综合噪声因素(包括元件精度的选择),有时,可能达不到上述比较理想分辨率的状况。
)。例如,显示值是68 °C,因为68 − 0.1− 0.0017 × 68 = 67.8864, 68 + 0.1+ 0.0017 × 68 =68.1156,所以实际温度可能是 (67.8864 ~ 68.1156) °C之间的一个值。注意,考虑电路设计的综合噪声因素(包括元件精度的选择),有时,可能达不到上述比较理想分辨率的状况。
3.2 数据记录
图4 显示的是STC 温控器测试的环境温度时所得,值为20.693 °C。表 1、表 2 则是该温控器连续测试的数据记录,一个用Pt100,另一个是E 型热电偶。这些值有时能保持~ 10 ~ 13 s ,一般~ 4 ~ 5 s ,表明该温控器的 Pt100 能分辨0.001 °C,热电偶能分辨0.014 °C。实现了高精度。

图4 用Pt100的温控器能分辨0.001 ℃
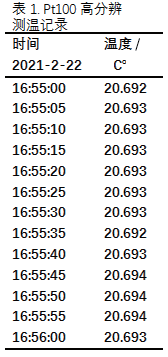
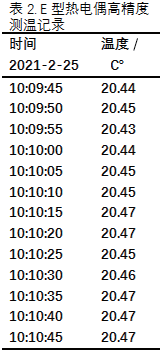
测试说明:测试时,为保持环境温度相对稳定,要减少空气流动,减少热源。并在温度稳定后(约10 ~ 15 min )开始测量。
4 结束语
温控器的高精度温度测控任重道远,探索包括四线Pt100 使用在内的更新的测温技术来提高测温精度将是本实验室的下一个前行目标。
参考文献:
[1] LTC2486-16-Bit 2-/4-Channel ΔS ADC with PGA and Easy Drive Input Current Cancellation[M/OL].ADI,(2014-
11:1,5,17)[2019-10-8].https://www.analog.com/media/en/technical-documentation/Data-sheets/2486fe.pdf.
[2] LTC2480-16-Bit ΔΣ ADC with Easy Drive Input Current Cancellation[M/OL].ADI,(2014-6:1)[2019-3-12].https://www.analog.com/media/en/technical-documentation/datasheets/2480fe.pdf.
[3] A Basic Guide to Thermocouple Measurements[M/OL].TI,(2014-11:4,6,9)[2019-10-8].https://www.ti.com/lit/an/sbaa274/sbaa274.pdf?ts=1593588456562&ref_url=https%253A%252F%252Fcn.Bing.com%252F.
[4] 中国国家标准管理委员会.GB∕T 16839.1-2018 热电偶第1部分:电动势规范和允差[S],北京:中国标准出版社.2018:1-67.
[5]中国国家标准管理委员会.GB/T 30121-2013 工业铂热电阻及铂感温元件[S].北京:中国标准出版社,2013:3-7。
[6]王昌世.高精度温度芯片Si7051在热电偶补偿中的应用[J].电子产品世界,2020(1):69-73.
[7]王昌世.通过计算分度函数及反函数实现热电偶高精度测温[J].电子产品世界,2021(2):69-71.
[8] MOGHIMI R.Low noise signal conditioning for sensorbased circuits[M/OL].ADI,(2010-9:P5)[2020-6-11].https://www.analog.com/media/en/technical-docum entation/ technical-articles/MS-2066.pdf
[9] STM32F10x_StdPeriph_Lib_V3.5.0[CP/OL],V3.5.0,STMicroelectronics,(2011)[2013].https://www.
st.com/content/st_com/en/products/embedded-software/mcu-mpu-embedded-software/stm32-embedded-software/stm32-standard-peripherallibraries/stsw-stm32054.html
[10] 甘英俊,周宏平.基于三线制的高精度热电阻测量电路设计[J],电子设计工程,2010(12):31-33.
[11] 一元四次方程的求根公式[EB/OL].[2020-6-29].http://ww w . 3 6 0 d o c . c om/ c o n t e n t / 1 5 / 0 2 0 9 / 0 2 / 1 5 3 4 1 2 2 7 _447355569.shtml1.
[12] 张莉,姜建国.牛顿法在Pt100铂热电阻温度计算中的应用特性分析[J].现代电子技术,2007(6):146-148.
[ 1 3 ] R M 0 0 0 8 [ M / O L ] . R e v 2 0 . S T M i c r o e l e c t r o n ics,(2018-12:159-196,699-751)[2021-2-9] https://www.st.com/resource/en/reference_manual/cd00171190-stm32f101xx-stm32f102xx-stm32f103xx-stm32f105xxand-stm32f107xx-advanced-arm-based-32-bit-mcusstmicroelectronics.pdf.
(本文来源于《电子产品世界》杂志2021年8月期)




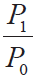





评论