AI讲座:神经网络的空间对应
1 神经网络的含义
人工神经网络(Artificial Neural Network)是一种模仿人类头脑处理信息方式的数学模型。这种人工神经网络(简称NN)的基本单元是神经元(Neuron),各个神经元与其他神经元互相连结在一起,一个神经元会受到多个其他神经元状态的冲击,也会将冲击传递给其他神经元。我们把人类头脑里的神经元简化成一个圆圈,而以箭号来表示冲击的传递。
这些神经元都位于层(Layer)中,最典型的神经网络模型包含三个部分:输入层(Input Layer)、隐藏层(Hidden Layer)和输出层(Output Layer)。其值(信息)从输入层的神经元传播到隐藏层的神经元,最终从输出层的神经元输出结果(Y)。如下图:
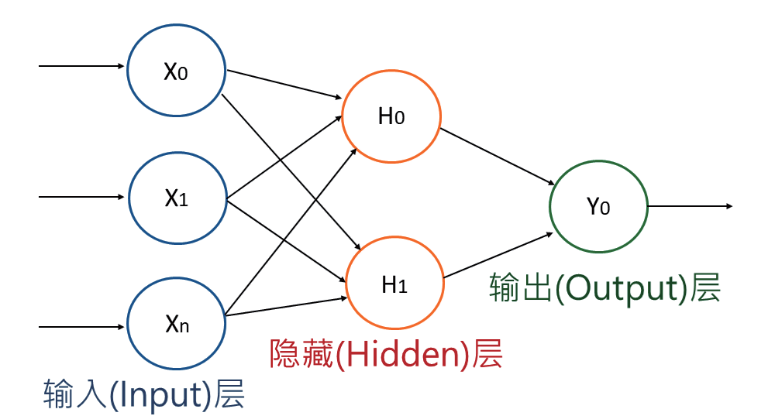
其中,x[ ] = [x0, x1, … ,xn] 表示输入信息,而Y0代表输出信息。
2 空间对应与神经网络
在本文里,将用神经网络图形来表达空间对应之关系,以及X*W+B=Y 的计算过程。例如,再上一期介绍过的简单空间对应关系(如下图)。请按下“寻找W&B”。这个NN 模型就迅速找出W 和B 值,如下:

此NN 模型找出来了W 值是:2,而B 值是:1。搭配 X*W + B = Y 公式,就可以掌握、记住上述的相关性(即规律性)了。于是,目前已知X、W和B 值了,就带入这个公式,如下图:
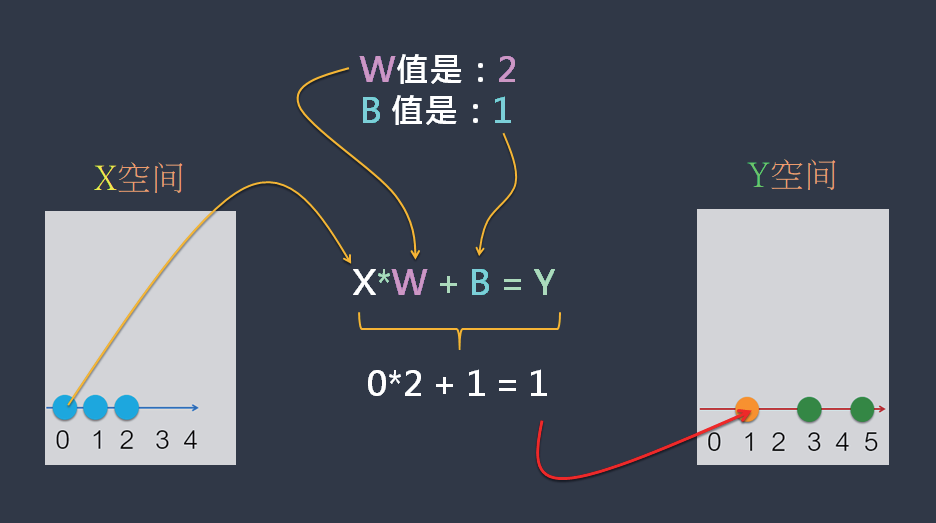
现在,就画上神经元的图形,来表示X*W + B = Y公式。如下:
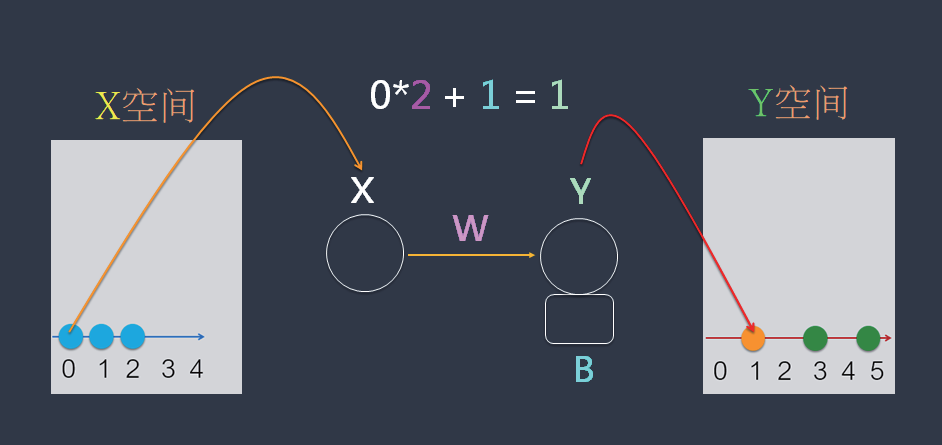
这时,X 神经元的值是:0。经过公式运算得到Y 值是:1。接下来,看看从二维的X 对应到一维的Z 空间的范例(如下图)。请按下“寻找W&B”,ML 就寻找出W=[0.5, 0.4],以及B=5。然后,经过X*W + B = Y公式的运算,得出Y 值,如下:
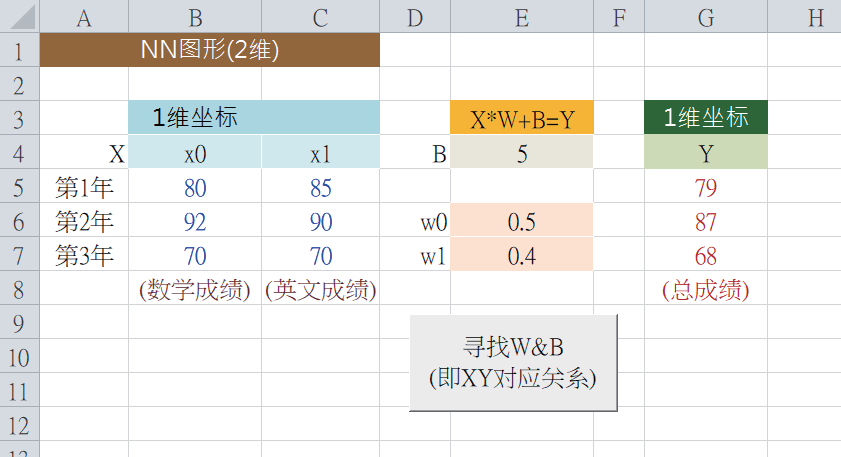
现在,使用神经网络图形来表达这个公式的运算。例如,拿X=[80, 85] 来计算出Y 值,如下:
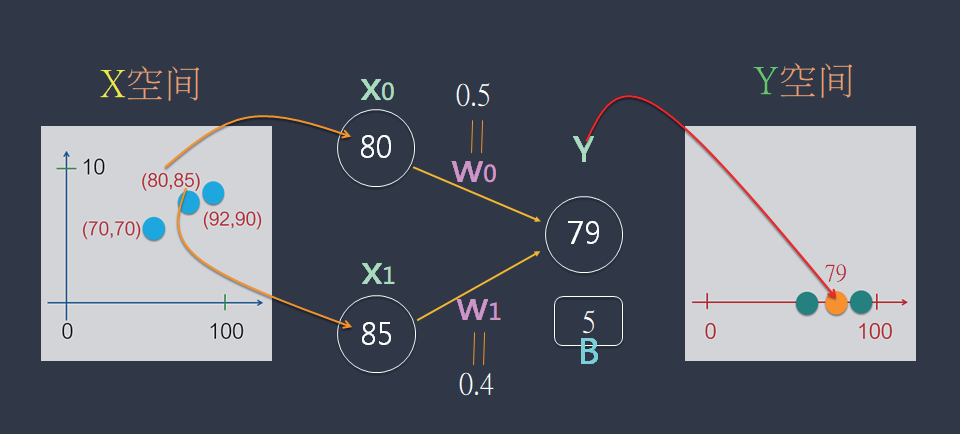
这图表达了“两两相乘& 求和 + B”的计算:
x0 * w0 + x1 * w1 + B= 80 * 0.5 + 85 * 0.4 + 5 = 79 = Y
于是,得出Y 值为:79。所以,利用神经网络图,让我们对于空间对应的计算过程变得非常清晰。
3 以NN来表达多维空间的对应
现在来看一个从三维空间,对应到一维空间的范例(如下图)。请按下“寻找W&B”,ML 就寻找出W=[0.5, 0.4],以及B=5。然后,经过X*W + B = Y 公式的运算,得出Y 值,如下:
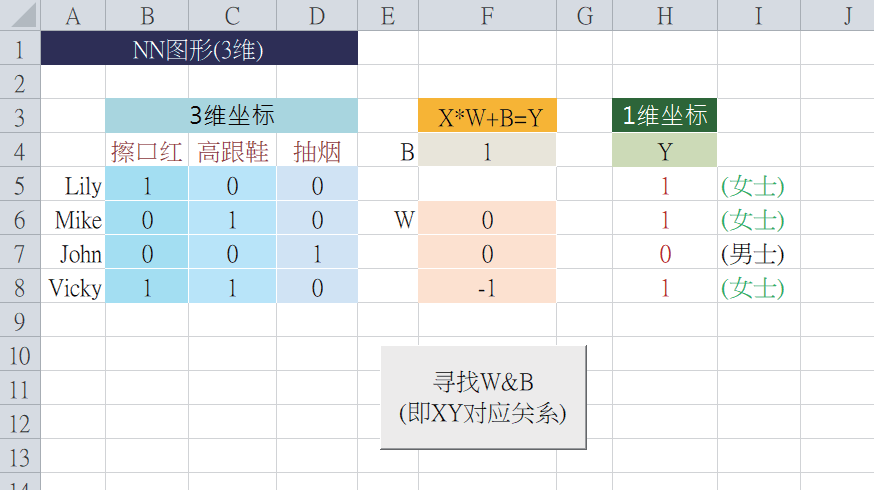
现在,使用神经网络图形来表达这个公式的运算。例如,拿X=[1, 1, 0] 来计算出Y 值,如下:
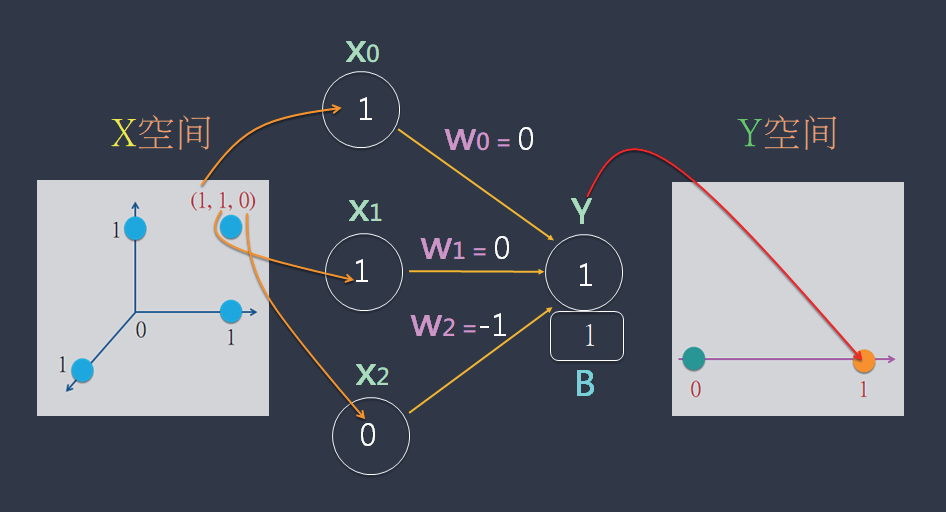
这图表达了“两两相乘& 求和 + B”的计算:
x0 * w0 + x1 * w1 + x2 * w2 + B= 1 * 0 + 1 * 0 + 0 * -1 + 1 = 1 = Y
于是,得出Y 值为:1。所以,利用神经网络图,让我们对于空间对应的计算过程变得非常清晰。现在来看一个从三维空间,对应到二维空间的范例(如下图)。请按下“寻找W&B”,ML 就寻找出W=[[0, 0], [0, 0],[-1, 1]],以及B=[1, 0]。然后,经过X*W + B = Y 公式的运算,得出Y 值,如下:
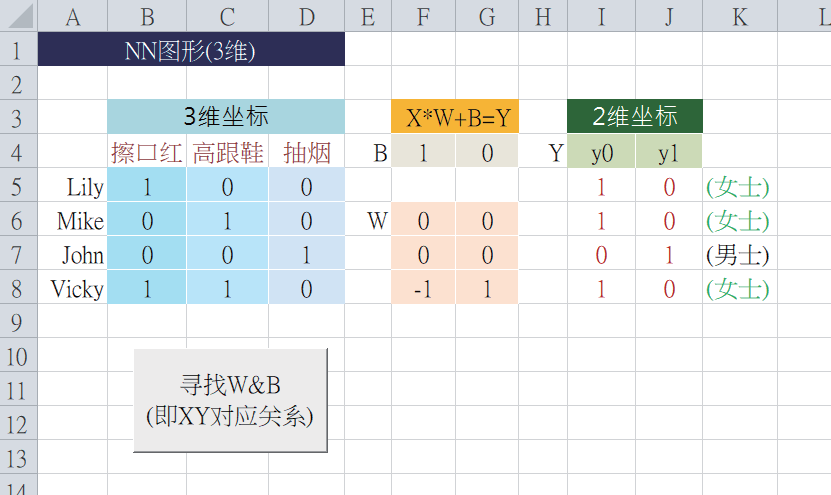
现在,使用神经网络图形来表达这个公式的运算。例如,拿X=[0, 0, 1] 来计算出Y 值,如下:
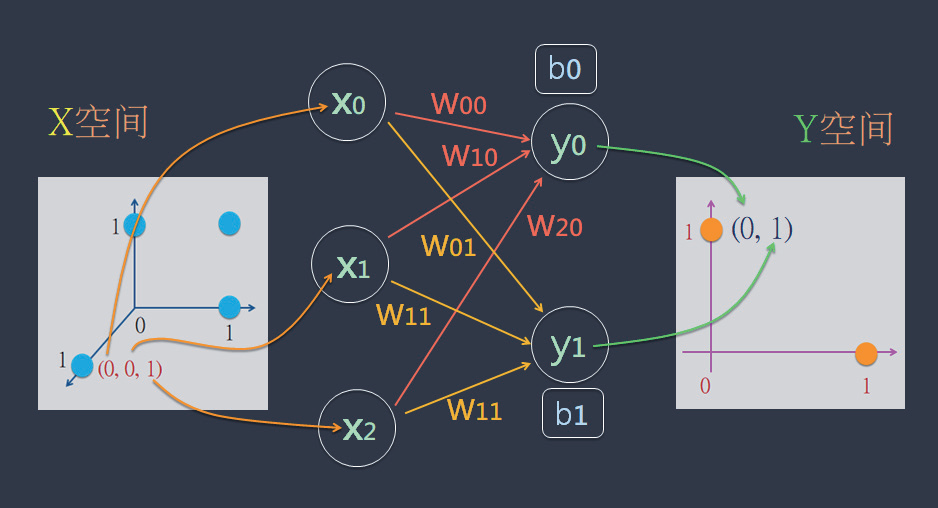
这图表达了两项“两两相乘& 求和 + B”的计算:
x0 * w00 + x1 * w10 + x2 * w20 + b0 = y0
x0 * w01 + x1 * w11 + x2 * w21 + b1 = y1
由于刚才已经寻找出W 和B 了,就把它们带入神经网络图里,则上图就相当于:
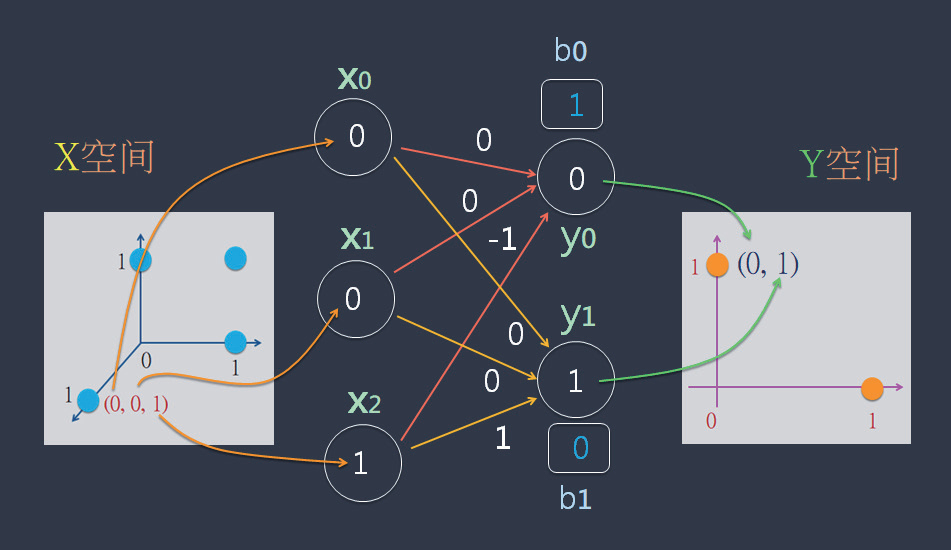
首先针对y0 而进行“两两相乘& 求和 + B”的计算:
x0 * w00 + x1 * w10 + x2 * w20 + b0= 1 * 0 + 1 * 0 + 0 * -1 + 1 = 1 = y0
然后,继续针对y1 而进行“两两相乘& 求和 + B”的计算:
x0 * w01 + x1 * w11 + x2 * w21 + b1= 1 * 0 + 1 * 0 + 0 * 1 + 0 = 0 = y1
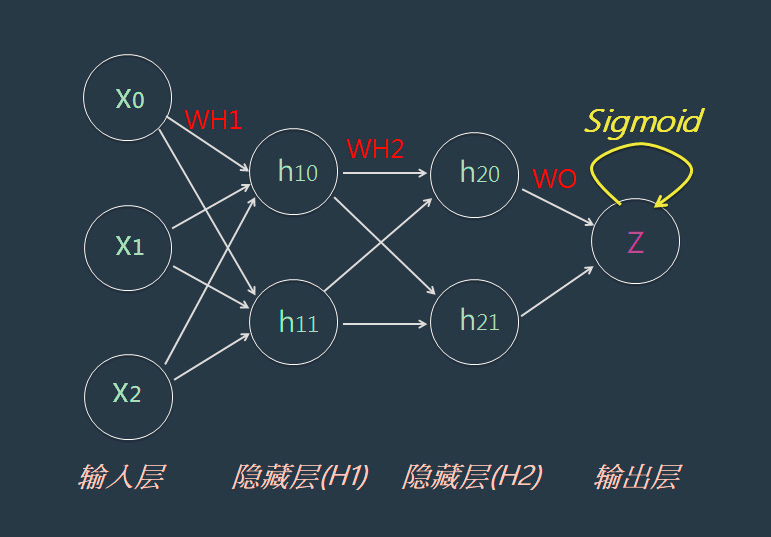
于是,得出Y=[1, 0]。从上述的范例里,您已经熟悉如何设计神经网络(NN)来表达两层的空间对应关系了。那就能扩大而设计出深度神经网络(如下图):
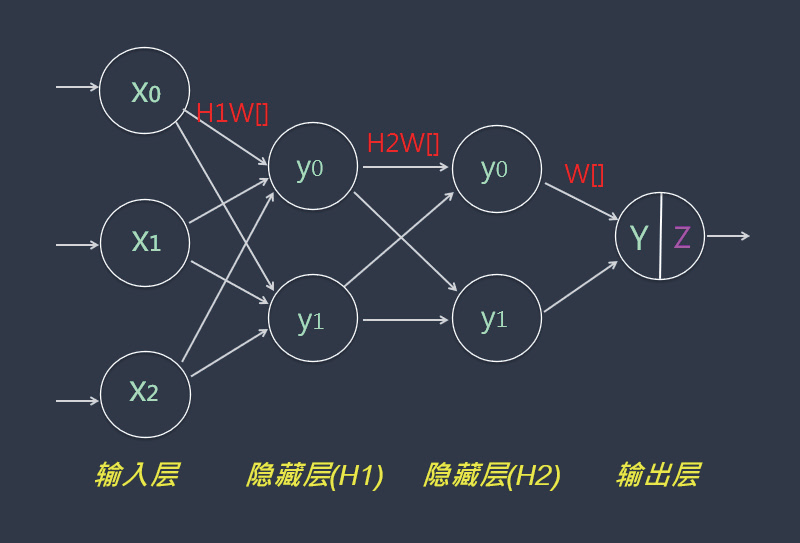
如此就能轻易实现深度学习中多层次的空间对应了。
(本文来源于《电子产品世界》杂志2021年8月期)












评论