基于SVM的永磁无刷直流电机无位置传感器控制
孙希凤,秦斌,王欣(湖南工业大学,湖南 株洲 412000)
本文引用地址:http://www.amcfsurvey.com/article/201912/408672.htm摘 要:由于传统带位置传感器直流电机容易受到外界的影响、体积较大且电机运行时电刷与换向器摩擦造成损耗会减少电机寿命,为了减小位置传感器对电机的影响,针对永磁无刷直流电机的位置检测问题,提出了基于支持向量机的永磁无刷直流电机无位置传感器控制方法。采集直流电机电压值电流值作为支持向量机的输入,功率器件开关状态变量作为输出,对模型进行训练,得到支持向量机的模型初始参数。然后将训练好的模型参数应用到直流电机中进行仿真,并与极限学习机仿真结果进行对比。结果显示支持向量机学习准确度较高,证明该方法能够较准确检测到直流电机转子位置。
关键词:直流电机;支持向量机;位置检测
*项目基金:国家自科科学基金项目(61673166);湖南省自然科学基金(2017JJ4022);湖南省自然科学基金(2018JJ4070)
0 引言
永磁无刷直流电机具有控制简单、调速性能好、效率高等特点 [1] ,因此广泛应用于汽车行业、工业、农业等领域。传统直流电机结构比较复杂,体积较大,不易于检修和维护,所以近年来直流电机的研究朝着简化电机结构,较少电机损耗等方向发展,而位置传感器的存在大大限制了无刷直流电机在恶劣环境及系统要求较高环境的应用 [2] 因此永磁无刷直流电机的位置检测成为直流电机研究的重点方向之一。
位置传感器在直流电机内部,负责检测直流电机转子位置并且将转子位置信息转化成电信号并输出控制功率器件开关。由于位置传感器具有非线性、易受外界环境影响等特点,无传感器转子位置检测比较困难。
近年来,各种无传感器位置检测方法得到深入研究。汤宁平、崔彬等 [3] 提出了高分辨的永磁无刷直流电机转子零初始位置检测方法,该方法适用于检测低速运行时的转子位置。窦满峰,苏超,谭博,方淳等提出优化磁链算法的位置检测方法 [4] 。李航等 [6] 提出的基于滞环切换的永磁无刷直流电机无位置传感器控制加宽了转子位置检测的速度范围。蒯松岩、张旭隆等 [7] 提出了使用神经网络对电机转子位置检测,该方法具有较好的动态性能,准确度也较高。王明超 [8] 将RBF神经网络应用于开关磁阻电机的转子位置控制,该方法控制精度较高。夏长亮,郭培健等 [9] 提出了将模糊遗传算法应用于无刷直流电机的自适应控制,改善了系统的抗干扰能力。王欣、梁辉等 [10] 提出了基于OSELM的无刷直流电机控制,该方法的优点是学习速度较快。本文采用SVM神经网络对无刷直流电机位置信息进行学习,并将学习好的模型应用于电机模型加以验证。
1 电机建模
电机系统的组成部分包含:电压源,逆变电路,电机,控制回路,传感器等。电机的模型建立:
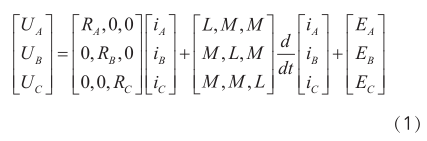
U是三相电压,R是三相电阻,L为三相电感,e为三相反电动势,M为三相互感。由于中性点处电流为0,所以有

将式3带入到式2中得到电机模型为:
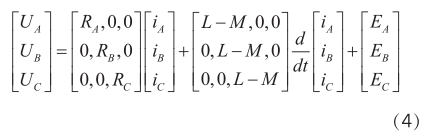
电磁转矩公式如下:

根据机械守恒可以得到:

2 支持向量机算法
2.1支持向量机原理
支持向量机是一种分类算法,它的目的是通过寻求结构化风险最小来提高学习泛化能力,实现经验风险和置信范围最小化,获取良好统计规律。支持向量机是一种二类分类模型,最早在1963年由苏联学者Vladimir N和Alexander Y提出的。
从图2可以看到两个平面之间存在间隙,间隙中间的红线为分离超平面,两个平面到分离超平面的距离是相等的,而要支持两个平面需要一些点,这些点叫做支持向量。
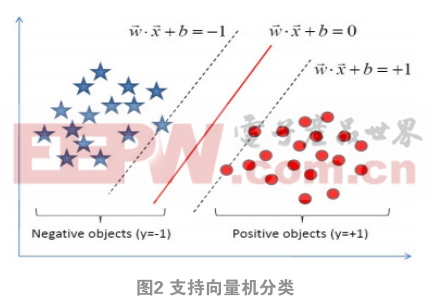
设分类函数 f(x)=wtx+b,f(x)=0是位于超平面上的点,则设 f(x)<0时 y = −1 , f (x)>0时, y =1 的数据点。
在超平面确定时的绝对值能表示点 x 到超平面的距离,而 wtx+b与 y 的符号是否一致能表示分类的准确性。
定义函数间隔为:

定义x为特征,y为结果标签,(w,b)关于训练集的函数间隔为超平面(w,b)关于训练集所有样本点 (xi,yi)的函数间隔最小值,其中 i 表示低 i 个样本,则有
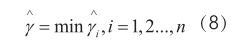
几何间隔:

x 0 为 x 投影到超平面的点, γ 为样本 x 到分类间隔的距离

几何间隔为:

最大间隔分类器目标为求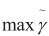 ,根据间隔定义有
,根据间隔定义有
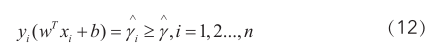
将式5带入式6,设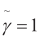 ,则最大间隔分类器目标转化为:
,则最大间隔分类器目标转化为:
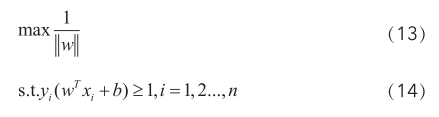
2.2 支持向量机无位置检测:
本文用SVM神经网络学习电机的转子位置信息,提取电机的电流和电压信息作为输入数据,霍尔传感器控制功率器件开关状态作为输出数据,对数据进行学习,获得初始支持向量机模型,并采集另外一组电流电压数据对支持向量机模型准确性进行验证,最后将训练好的模型应用到电机中,基于SVM的永磁无刷直流电机无位置传感器数据训练如下:
数据采集:试验采集电机电压电流参数4 000组数据,将这些数据分为两组,每组2 000组数据,一组用于训练,另一组用于测试。试验的数据包括:输入包含电压数据 {UA(K),UB(K),UC(K),UA(K-1),UB(K-1),UC(K-1)} ,电流数据 {iA(K),iB(K),iC(K),iA(K-1),iB(K-1),iC(K-1)} 。采集位置传感器的电机位置信息数据,然后将数据进行逻辑转换从而得到功率管开关状态{g1,g2,g3,g4,g5,g6,g7,g8,g9,g10,g11,g12},支持向量机的输出为得到的功率管的状态,每个功率管状态只有0和1两种状态。
支持向量机实验结果如图3~5.
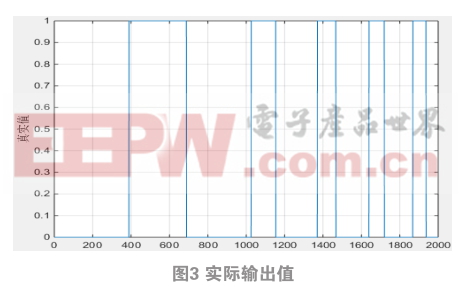
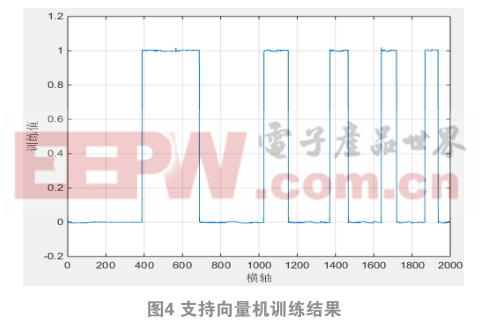

3 实验结果
3.1 模型应用
将算法训练好之后,需要将训练好的算法加到电机模型中,对电机进行控制,算法应用通过S函数实现。
实验电机参数为:Ud为540 V,为0.137 Ω ,R2为0.31Ω,L1为0.76 mH,L2为1.81 mH,Ke1为1.26 V.r/s,Ke2为1.94 V.r/s,转矩为70 N.m。
电机模型仿真结果:

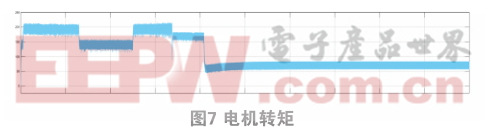
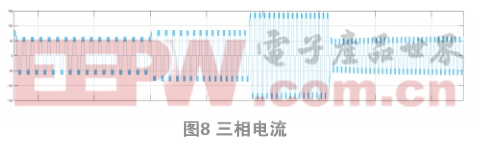
应用仿真图如下:

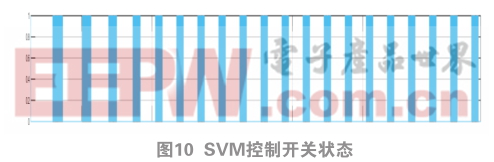
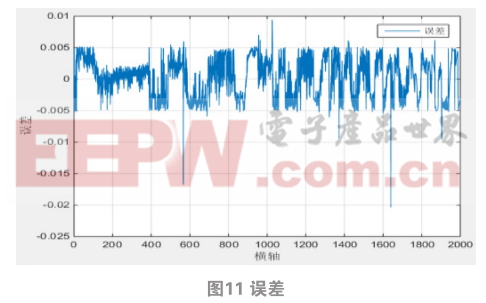
3.2 OSELM与SVM实验结果对比
为了验证支持向量机算法的优点,将支持向量机算法和极限学习机进行对比,对比的内容包括两种算法的运行时间和运行误差两方面,这里误差使用平方差表示,对比结果如下表:
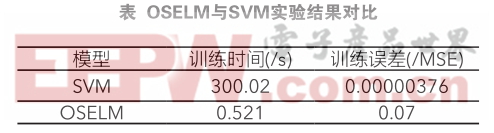
从上表中可以明显看到支持向量机误差十分小,其误差比在线极限学习机小很多,证明该算法精度很高,对转子位置预测更准确,而极限学习机消耗时长较小。
4 结论
本文用支持向量机对直流电机位置信息进行学习,并将训练好的模型用于电机模型中加以验证,证明了支持向量机算法应用于电机无位置控制的可行性,且与极限学习机相比较,可以看出支持向量机学习位置信息精度较高。
参考文献
[1] 杨贵营.基于FPGA的准正弦波无刷直流电机控制及系统实现[D]. 成都:西南交通大学, 2014.
[2] 史婷娜,田洋,夏长亮.基于小波网络的永磁无刷直流电机无位置传感器控制[J].天津大学学报,2007,40(2):190-194.
[3] 汤宁平,崔彬.高分辨的永磁无刷直流电机转子零初始位置检测方法[J].电工技术学报,2013,28(10):90-96.
[4] 窦满峰,苏超,谭博,等.优化磁链算法的稀土永磁无刷电机位置检测方法[J].微电机,2017,(5):81-86.
[5] 刘鸿.梯形波永磁无刷直流电机的两种控制方案及其相关问题研究[J].济南:山东大学,2015.
[6] 李航,付朝阳.基于滞环切换的永磁无刷直流电机无位置传感器控制[J].微电机, 2017,15(8):18-22.
[7] 蒯松岩,张旭隆,王其虎,等.开关磁阻电机神经网络无位置传感器控制[J].电机与控制学报,2011.
[8] 王明超.基于RBF神经网络的开关磁阻电机无位置传感器控制及单神经元PID控制[D].天津:天津大学,2004.
[9] 夏长亮,郭培健,史婷娜,等. 基于模糊遗传算法的无刷直流电机自适应控制[J].中国电机工程学报,2005,(11):129-133.
[10] 王欣,梁辉,秦斌.基于OSELM的无刷直流电机无位置传感器控制[J].电机与控制学报,2018,22(11):82-88.
本文来源于科技期刊《电子产品世界》2020年第01期第39页,欢迎您写论文时引用,并注明出处。







评论