一种基于状态观测器的PMSM速度观测算法
王远洋 王 卫(湖南工业大学 电气与信息工程学院,湖南 株洲 412008)
本文引用地址:http://www.amcfsurvey.com/article/201911/407675.htm摘 要:为了改善低线数码盘的测速精度及码盘固有的相位滞后问题,提出了一种基于状态观测器的速度观测算法。该算法以电机转矩电流和机械角度作为输入量,根据电机的数学模型和机械特征方程,构建速度观测器,来实现对永磁同步电机速度的精确控制。仿真及实验结果表明:该方法与码盘M法测速相比,测得的速度更加精确,并且超调量小,响应快,能起到相位补偿的作用,解决了码盘固有的相位滞后问题,同时,在负载发生变化时系统仍然能保持很好的稳定性和控制精度。
关键词:永磁同步电机;码盘;速度观测器;状态观测器;M法测速
0 引言
速度是永磁同步电机控制系统中的一个重要参数,速度检测的精准性和快速性直接影响着控制系统的性能[1] 。而速度的测量元件大多是码盘。利用码盘作为检测元件计算电机速度的方法主要有 M 法、T 法、M/T 法[2-3] 以及变M/T 法 [4-6] 。这些方法都是通过对码盘获取到的脉冲周期和频率进行计算而得到电机速度的,当电机处于低速状态和码盘分辨率较低时,这些方法容易出现测速不精确和与实际指令跟随差的问题。
为了让电机在低速和码盘分辨率低的情况下也能实现对电机速度的精确控制,需要对电机的瞬时速度进行检测。电机的瞬时速度检测方法可分为两类,一类是通过检测元件检测位置的当前周期值和上个周期值然后对电机当前的瞬时速度进行估计。文献 [7] 中电机当前周期的瞬时速度是通过对电机的平均速度来进行估算得到的,以此来补偿速度检测所带来的延时;文献通过码盘位置值估算电机的加速度 [8] ,然后对加速度进行积分得到电机的瞬时速度。这些方法不受电机数学模型的影响且只利用了码盘的脉冲信号。因此,电机参数变化对这类方法的测量精度无影响,它只与码盘的线数和算法本身有关。另一类是利用电机的数学模型和机械特征方程构造速度观测器 [9] ,对电机的瞬时速度进行观测,这类方法对系统速度具有预测特性,可以提高系统速度环的响应带宽,大体有全阶状态观测器 [10] 和降阶状态观测器[11] 等。降阶状态观测器算法较简单,易实现,但是对系统噪声和输入噪声敏感,而全阶状态观测器,对系统噪声及输入噪声有很强的抑制作用,算法复杂,但随着处理器性能的提升,让该算法的实现成为了可能。本文采用全阶状态观测器作为速度观测器的方法。
2 PMSM数学模型的建立
2.1 数学模型的前提条件
本文以表贴式的PMSM作为研究对象,由于在工程使用过程当中,PMSM有非线性、约束条件多的特点,所以为了便于分析和研究,在对PMSM基本数学模型进行建立的时候需要做一定的假设:
1)不计铁芯以及磁路的饱和程度;
2)忽略电机中电枢铁芯的涡流损耗;
3)通入空间相隔120电角度的对称三相电。
2.2 PMSM数学模型
表贴式三相PMSM在 d - q 静止坐标系下等效模型可以表示为 [11] :
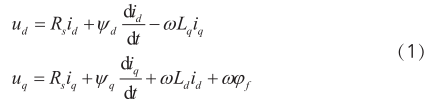
式中: ud uq、分别为定子电压在 d-q轴的分量; R s为电枢绕组电阻; Ld Lq、分别是 d-q轴电感分量; L s 为电枢电感; id iq、分别为定子电流 d-q轴的分量; φ d 、φ q 为定子磁链的 d-q轴分量; ϕ f 为转子磁链; ω 为电角速度。
2.3 PMSM机械特性方程
PMSM的电机的转矩和运动学方程为:
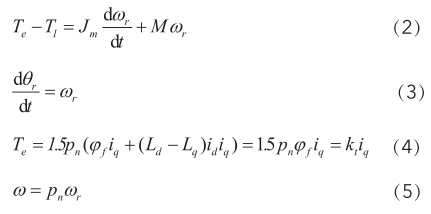
式中: J m 为转动惯量; M 为黏滞摩擦系数; T e 为电磁转矩; T l 为负载转矩; k t 为电机转矩常数; p n 为电机极对数; ω r 为电机的机械角速度; θ r 为电机的机械角度。
3 状态观测器的设计
3.1 状态观测器基本原理
状态观测器又叫状态重构,其基本思想就是用可以测量的参数作为输入量,通过对状态进行重构,使得估计得到的状态值逼近真实的状态值 [12] 。闭环状态观测器的方框图如图1所示。
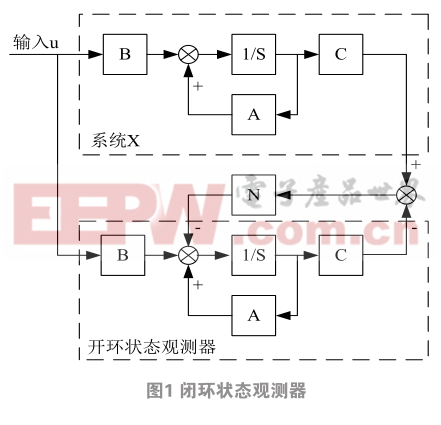
此时,其状态方程变为
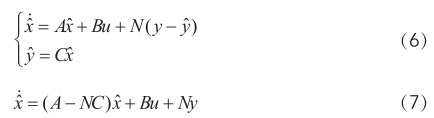
其观测误差方程为:

由式(8)可知误差特征方程为

由控制理论可知,想要系统稳定,就要使式(9)的极点全部分布在s平面左平面,而且系统的极点可以影响到误差的收敛速度。因此,要使误差能够快速的收敛到0,只要通过引入反馈值并且选择合适的 N ,就能达到对状态估计的作用,而不受状态初值的影响。
3.2 状态观测器的设计
忽略黏滞摩擦系数M,式(3)可重写为:

式(10)可转化为:

负载的变化一般是相对较缓慢的,所以可以认为负载在一个控制周期内是没有变化的,即:

另外,由运动学定理可知电机转子在一个控制周期T a 上的角位移方程如下式:
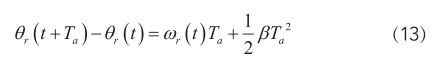
由于控制周期 T a 很小,则(13)可以写成如下形式:

把式(11)带入式(14)得:
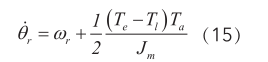
将式(11)(12)和(15)改写成矩阵形式为:
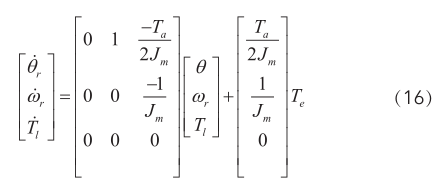
根据(6)(16)式可构造全阶状态观测器模型为:
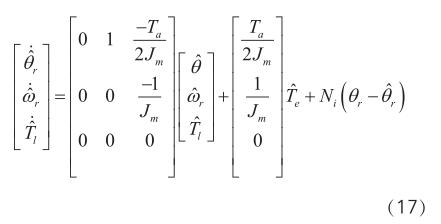
上式中N i 为观测器的比例增益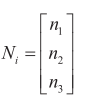
根据(16)(17)算得其误差方程为:
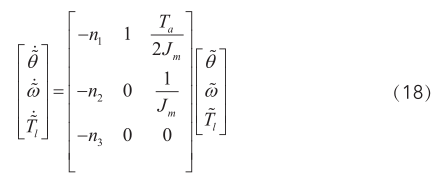
根据(18)得误差状态方程的特征方程为:
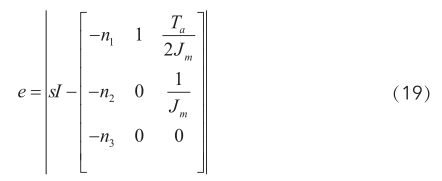
通过配制 n 1 , n 2 , n 3 的值可以使系统稳定并控制其收敛速度。
式(17)离散化到后得到的方程式为:
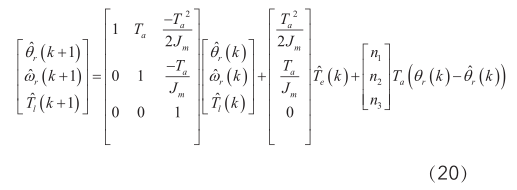
由控制理论可知要使系统收敛只要系统的极点在s平面左半平面,但为了达到想要的效果,需要选择合适的极点,也就是要让速度观测误差收敛速度比速度的响应要快,即观测器的极点比速度闭环的极点更远离原点。但过大的观测器极点值会引起系统噪声,导致观测误差,因此对观测器极点的选择要结合这两方面考虑[13] 。
4 系统仿真及实验结果
4.1 系统仿真模型
为了便于对比,Simulink 仿真与实验平台采用的算法和电机参数相同。仿真和实验平台中给定速度环的速度指令也相同。仿真及其实验电机参数见表1。
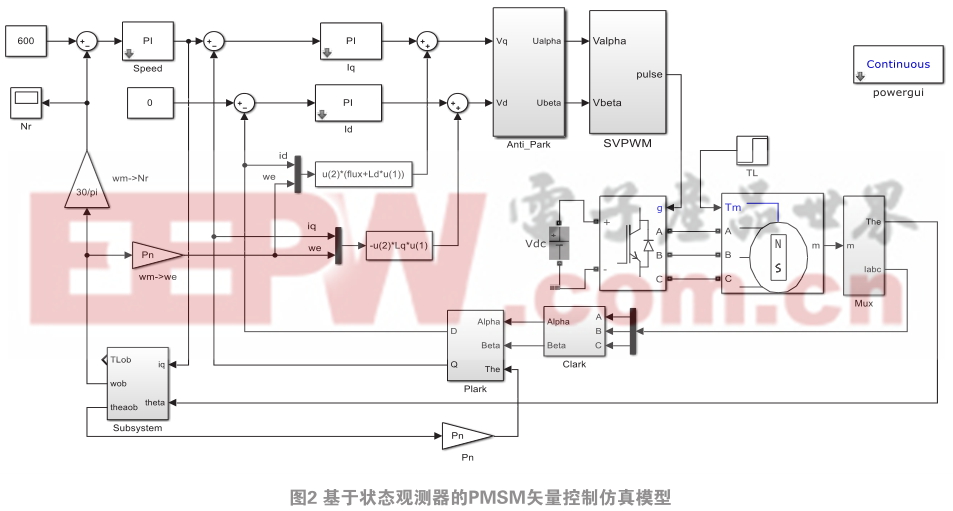
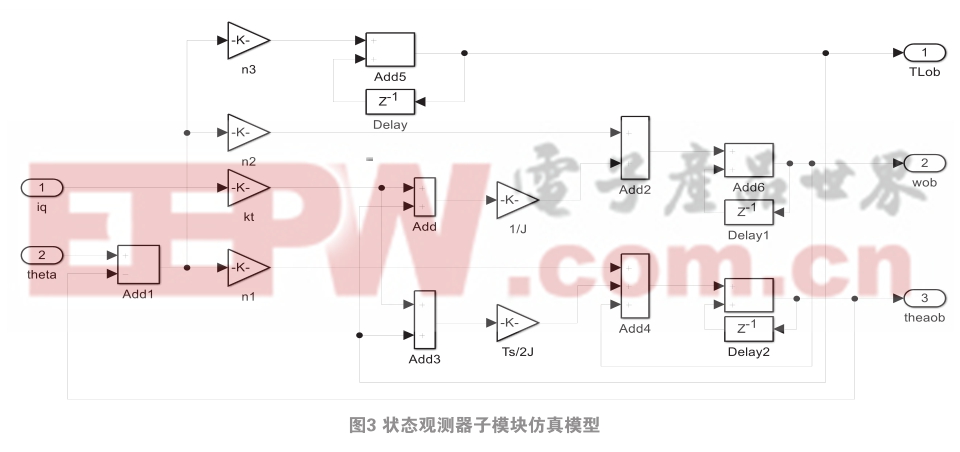
在Matlab/simulink环境下,根据前面的理论分析建立了基于状态观测器的PMSM矢量控制仿真模型,其仿真模型如图2所示,PMSM矢量控制系统的电流控制方法为 i d = 0 控制,控制周期为125 μs ,状态观测器子模块仿真模型如图3所示。
4.2 仿真结果分析
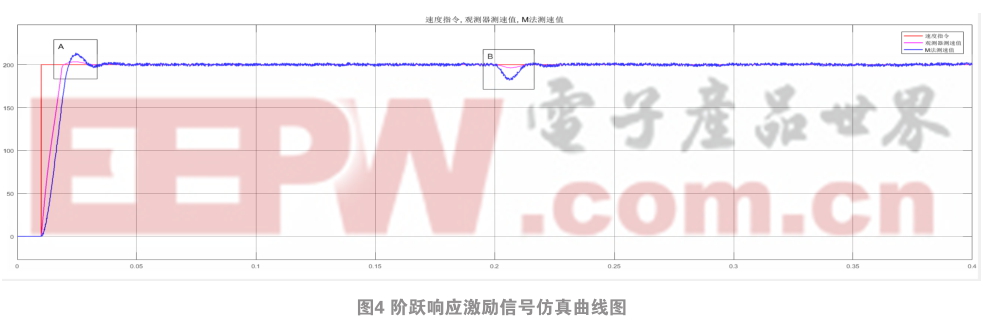
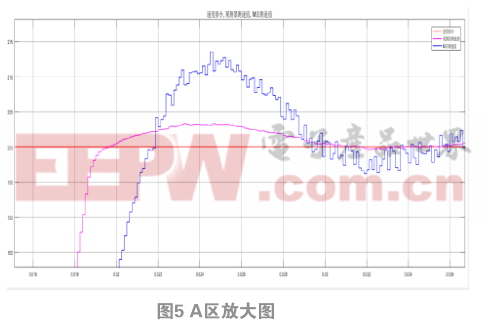
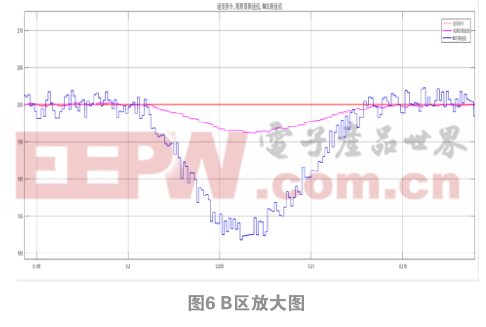
图4是速度指令为阶跃响应激励信号时速度观测值与码盘M法测速值曲线对比图,系统控制周期为125 μs 。从图中可以看出,系统在0.01 s时给出速度指令,转速期望值为200 r/min,并且在0.2 s时加入了2 N.m的扰动负载转矩。从整体波形图可以看出,码盘M法测速值比速度观测值转速波动大得多。从A区放大图中可看出,速度观测值大约在0.019 6 s达到期望值,转速最大值为203 r/min,超调为1.5%,并且大致在0.031 5 s回归稳定状态,而码盘M法测度值大约0.021 8 s才达到期望值,转速最大值为214 r/min,超调达到了7%,且大致在0.033 2 s才回归稳定状态,对比两组数据发现速度观测器得到的速度响应快,超调小。在0.2 s时加上2N.m的扰动负载转矩,在B区放大图中可以看到速度观测值很快达到稳定状态,且没有出现较大的转速波动,而码盘M法测速值,达到稳定状态时间长,且转速出现了很大的波动。综上所述,基于状态观测器的速度观测值具有更快的响应效率,更高的检测精度,更强的平稳性。
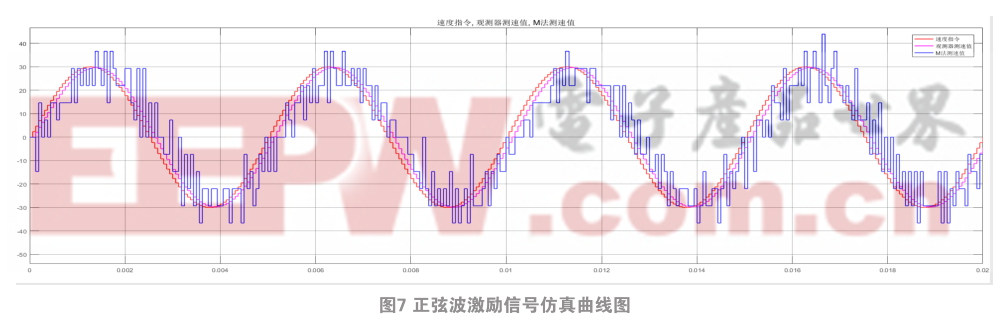
为了更加直观地看到观测器测速与码盘M法测速的区别,给系统设定幅值为-30-30 r/min,频率为200 Hz的正弦波激励信号,从图7可知,速度观测值和码盘M法测速值都能很好地跟随速度指令,但是速度观测值跟随的更紧,比码盘M法测速值要超前一个周期,同时,转速波动要小很多。因此观测器测速能有效地解决码盘测速固有的相位滞后问题,且测速精度更高。
4.3 实验结果
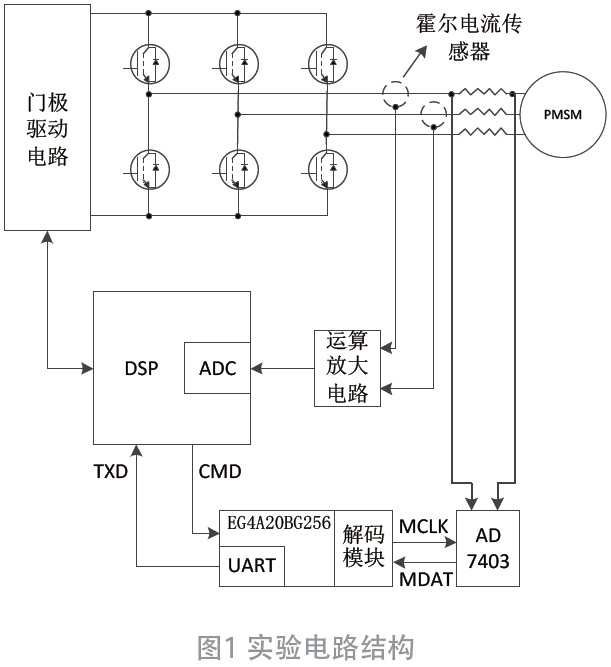
为了检验状态观测器在实际系统中的可行性,进行了实验验证,实验平台如图 8 所示,采用 ST公司的 32位RAM控制平台STM32F407作为主控芯片,系统主要包括上位PC机,表贴式永磁同步电机,RAM控制板,功率板等,系统控制周期为125μs。速度指令及电机参数与仿真系统一致,实验数据通过通讯的方式由 RAM传送到上位PC机。

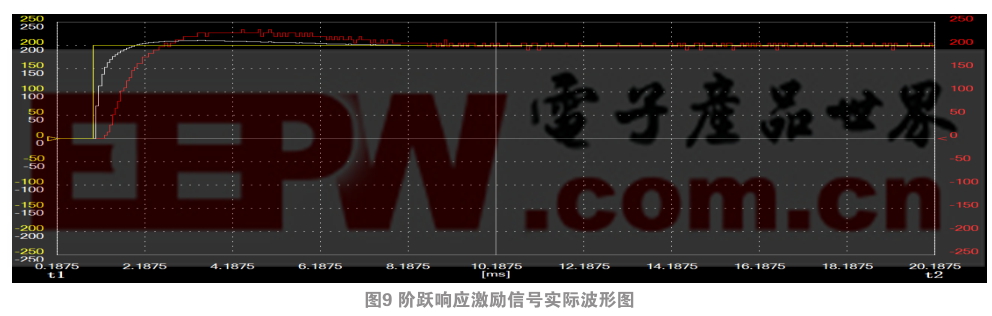
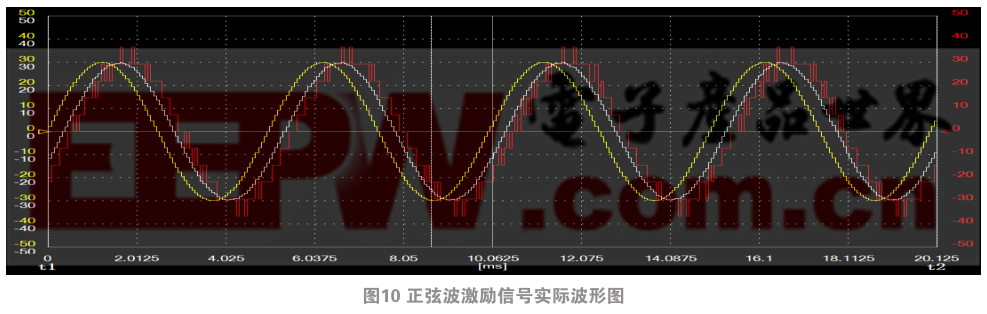
图9、图10分别是速度指令为阶跃响应激励信号和正弦波激励信号时电机在实际系统中速度波形图,其中,黄色曲线为速度指令,白色曲线为观测器测速值,红色曲线为M法测速值,可以看到在实际系统中速度观测器测得的速度值波动小,而且速度曲线较平滑,说明其比码盘M法测速更具扰动修正能力。另外它比码盘M法测速的速度值更接近速度指令值,能起到相位补偿的作用。对比可知,实验结果与仿真结果基本一致,这充分证明了基于状态观测器的速度观测算法在实际系统中的有效性。
5 结论
本文对永磁同步电机测速方法进行了研究和分析,提出了利用状态观测器作为测速方法,并对状态观测器进行设计,通过对状态观测器测速方法和码盘M法测速方法进行比较。仿真及实验结果表明,使用状态观测器的测速方法比码盘M测速法的方法有更好的稳定性,更高的精准性和更强的适应性,并且状态观测器有相位超前的功能,能很好地解决码盘测速固有的相位滞后问题,起到相位补偿的作用,同时状态观测器能在码盘线数较低的前提下实现对速度的精确控制,能大大地降低产品的成本,具有很大的实际意义。
参考文献
[1] 杨兴华,姜建国.永磁同步电机精确瞬时速度检测[J].电工技术学报,2011,26(04):71-76.
[2] Tsuji T, Mizuochi M, Nishi H, et al.A velocity measurement method foracceleration control[C]. 31st IndustrialElectronics Society Annual Conferenceof IEEE, 2005: 1943-1948.
[3] 李勇,潘松峰.基于DSP的M/T法测速研究[J].工业控制计算机,2018,31(05):145-146.
[4] 徐张旗,陶家园,王克逸,简慧杰.基于卡尔曼滤波的新型变“M/T”编码器测速方法[J].新技术新工艺,2018(09):28-31.
[5] 王海勇,鲍远慧.一种变M/T测速方法的研究与实验[J].测控技术,2014,33(05):146-149.
[6] 赵帅,肖金壮,郭一.基于改进型卡尔曼滤波的电机速度数据处理方法[J].微特电机,2018,46(09):80-82.
[7] Wang Gaolin, Xu Dianguo, Yu Yong,et al. Low speed control of permanentmagnet synchronous motor based oninstantaneous speed estimation[C].The Sixth World Congress on IntelligentControl and Automation, 2006, 2: 8033-8036.
[8] Lee Se Han, Song Jae Bok. Accelerationestimator for low-velocity and low-acceleration regions based on encoderposition data[J]. IEEE/ASME Transactionson Mechatronics, 2001, 6(1): 58-64.
[9] 张永澜. 状态观测器在伺服控制系统中的应用研究[D].哈尔滨:哈尔滨工业大学,2007.
[10] 罗桂山.基于全阶状态观测的无速度传感器矢量控制仿真[J].机电设备,2017,34(03):26-30.
[11] 刘玉燕,刘吉臻,周世梁.基于降阶状态观测器的压水堆功率自抗扰控制[J].中国电机工程学报,2017,37(22):6666-6674+6779.
[12] 沈阳,舒志兵,朱尔立,吴晨军,高春宝.Luenbeger速度观测器在交流伺服系统中的设计与研究[J].微电机,2016,49(03):87-89.
[13] 宋成. 交流永磁同步电机的速度观测器研究及实现[D].哈尔滨:哈尔滨工业大学,2011.
本文来源于科技期刊《电子产品世界》2019年第12期第68页,欢迎您写论文时引用,并注明出处。




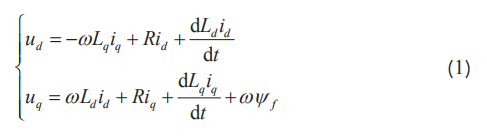



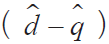

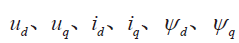


评论